問題3.4.2
次の曲線の長さを求めよ。
(1) $\begin{cases} x=t \cos \dfrac{1}{t} \\ y=t \sin \dfrac{1}{t} \end{cases} \ \ \ (1 \leqq t \leqq 2)$
(2) $\begin{cases} x=3t^2 \\ y=3t-t^3 \end{cases} \ \ \ (0 \leqq t \leqq 2)$
《ポイント》
滑らかな曲線$C$:$\begin{cases} x=X(t) \\ y=Y(t) \end{cases} \ \ \ (a \leqq t \leqq b)$ の長さは$$\displaystyle \int_{a}^{b} \sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}dx$$で表されます。これも3.4.1と同様に区分求積法によって証明することができます。パラメータ表示された曲線は形状をイメージしにくいことが多いですが、対称性を利用できる場合も少なくないので、計算を省力化するためにも概形を大まかに把握しておくのが好ましいでしょう。
《解答例》
(1)
求める曲線$C$:$\begin{cases} x=t \cos \dfrac{1}{t} \\ y=t \sin \dfrac{1}{t} \end{cases} \ \ \ (1 \leqq t \leqq 2)$ の長さを$l$とすると、
$\begin{align}&l = \displaystyle \int_1^2 \sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}dt \\
&= \displaystyle \int_1^2 \sqrt{\left(\cos \dfrac{1}{t}+\dfrac{1}{t}\sin \dfrac{1}{t}\right)^2+\left(\sin \dfrac{1}{t}-\dfrac{1}{t}\cos \dfrac{1}{t}\right)^2}dt \\
&= \displaystyle \int_1^2 \sqrt{\cos^2 \dfrac{1}{t}+\sin^2 \dfrac{1}{t}+\dfrac{1}{t^2}\left(\sin^2 \dfrac{1}{t}+\cos^2 \dfrac{1}{t}\right)}dt \\
&= \displaystyle \int_1^2 \sqrt{1+\dfrac{1}{t^2}}dt \\
&= \displaystyle \int_1^2 \dfrac{\sqrt{t^2+1}}{t}dt \ \ \cdots \cdots (*) \end{align}$
ここで $\sqrt{t^2+1}=u$ と置くと、$t:1 \to 2$ のとき $u:\sqrt{2}\to\sqrt{5}$ であり、$tdt=udu$ が成り立つから、
$\begin{align}&(*)=\displaystyle \int_{\sqrt{2}}^{\sqrt{5}} \dfrac{u^2}{u^2-1}du \\
&=\displaystyle \int_{\sqrt{2}}^{\sqrt{5}} \left\{1+\dfrac{1}{2}\left(\dfrac{1}{u-1}-\dfrac{1}{u+1}\right)\right\}du \\
&=\left[u+\dfrac{1}{2}(\log|u-1|+\log|u+1|)\right]_{\sqrt{2}}^{\sqrt{5}} \\
&=\sqrt{5}-\sqrt{2}+\dfrac{1}{2}\left(\log\dfrac{\sqrt{5}-1}{\sqrt{5}+1}-\log\dfrac{\sqrt{2}-1}{\sqrt{2}+1}\right) \ \ \cdots \cdots \text{(答)} \end{align}$
※教科書の答えと形が異なりますが値は同じです。後ろの部分を以下のように式変形すれば同じであることが確かめられます。$$\begin{align} & \quad \dfrac{1}{2}\left(\log\dfrac{\sqrt{5}-1}{\sqrt{5}+1}-\log\dfrac{\sqrt{2}-1}{\sqrt{2}+1}\right) \\ &= \dfrac{1}{2}\left(\log\dfrac{(\sqrt{5}-1)^2}{5-1}-\log\dfrac{(\sqrt{2}-1)^2}{2-1}\right) \\ &= \dfrac{1}{2}\left(\log \left(\dfrac{\sqrt{5}-1}{2}\right)^2-\log (\sqrt{2}-1)^2\right) \\ &= \log \left(\dfrac{\sqrt{5}-1}{2}\right)-\log (\sqrt{2}-1) \\ &= \log (\sqrt{5}-1) – \log (\sqrt{2}-1) – \log 2 \end{align}$$
※曲線$C$:$\begin{cases} x=t \cos \dfrac{1}{t} \\ y=t \sin \dfrac{1}{t} \end{cases} \ \ \ (1 \leqq t \leqq 2)$ の概形は以下のようになります。
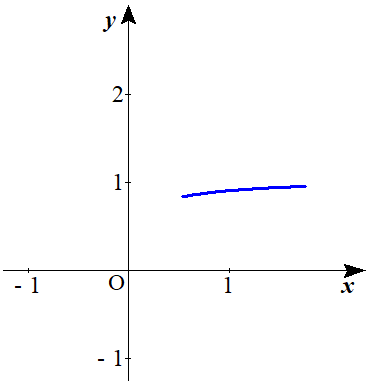
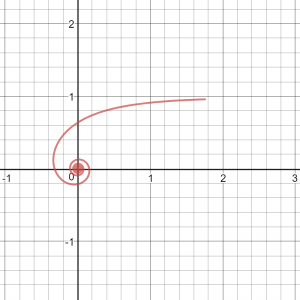
なお、$0 \leqq t \leqq 2$ の範囲で図示すると以下のように螺旋を描きます。
(2)
求める曲線$C$:$\begin{cases} x=3t^2 \\ y=3t-t^3 \end{cases} \ \ \ (0 \leqq t \leqq 2)$ の長さを$l$とすると、
$\begin{align}&l = \displaystyle \int_0^2 \sqrt{\left(\dfrac{dx}{dt}\right)^2+\left(\dfrac{dy}{dt}\right)^2}dt \\
&= \displaystyle \int_0^2 \sqrt{(6t)^2+(3-3t^2)^2}dt \\
&= \displaystyle \int_0^2 3\sqrt{1+2t^2+t^4}dt \\
&= \displaystyle 3\int_0^2 \sqrt{(1+t^2)^2}dt \\
&= \displaystyle 3\int_0^2 (1+t^2)dt \\
&=3\left[t+\dfrac{1}{3}t^3\right]_0^2 \\
&=14 \ \ \cdots \cdots \text{(答)} \end{align}$
※曲線$C$:$\begin{cases} x=3t^2 \\ y=3t-t^3 \end{cases} \ \ \ (0 \leqq t \leqq 2)$ の概形は以下のようになります。

復習例題未設定
