問題5.1.2b
積分を計算せよ。
(5)$\displaystyle \iint_{D} xy^2\ dxdy$ $D:0 \leqq y \leqq x \leqq 1$
(6)$\displaystyle \iint_{D} (2x-y)\ dxdy$ $D:x \leqq y \leqq 2x$、$x+y \leqq 3$
(7)$\displaystyle \iiint_{D} z\ dxdydz$ $D:0 \leqq x \leqq 1$、$0 \leqq y \leqq 1-x$、$0 \leqq z \leqq 1-x-y$
(8)$\displaystyle \iiint_{D} y\ dxdydz$ $D:x \geqq 0$、$y \geqq 0$、$z \geqq 0$、$x+2y+3z \leqq 6$
《ポイント》
累次積分の計算練習です。
《解答例》
(5)$\displaystyle \iint_{D} xy^2\ dxdy$ $D:0 \leqq y \leqq x \leqq 1$
$\begin{align}&\ \ \ \ \displaystyle \iint_{D} xy^2\ dxdy \\ &=\displaystyle \int^{1}_{0} dy \int^{1}_{y} xy^2\ dx \\ &=\displaystyle \int^{1}_{0}\left[\dfrac{1}{2}x^2y^2\right]^{1}_{y}\ dy \\ &=\dfrac{1}{2}\displaystyle \int^{1}_{0}(y^2-y^4)\ dy \\ &=\dfrac{1}{2}\left[\dfrac{1}{3}y^3 -\dfrac{1}{5}y^5\right]^{1}_{0} \\ &=\dfrac{1}{15} \ \ \cdots \cdots \text{(答)}\end{align}$
(6)$\displaystyle \iint_{D} (2x-y)\ dxdy$ $D:x \leqq y \leqq 2x$、$x+y \leqq 3$
領域$D$を図示すると以下のようになる。
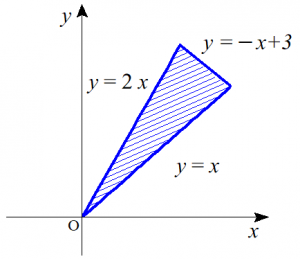
$\begin{align}&\ \ \ \ \displaystyle \iint_{D}(2x-y)\ dxdy \\ &=\displaystyle \int^{1}_{0} dx \int^{2x}_{x} (2x-y)\ dy+\int^{\frac{3}{2}}_{1} dx \int^{-x+3}_{x} (2x-y)\ dy \\ &=\displaystyle \int^{1}_{0}\left[2xy-\dfrac{1}{2}y^2\right]^{2x}_{x}\ dx +\int^{\frac{3}{2}}_{1}\left[2xy-\dfrac{1}{2}y^2\right]^{-x+3}_{x}\ dx \\ &=\displaystyle \int^{1}_{0}\dfrac{1}{2}x^2\ dx +\int^{\frac{3}{2}}_{1}\left(-4x^2+9x-\dfrac{9}{2}\right)\ dx \\ &=\dfrac{1}{2}\left[\dfrac{1}{3}x^3\right]^{1}_{0}+\left[-\dfrac{4}{3}x^3+\dfrac{9}{2}x^2-\dfrac{9}{2}x\right]^{\frac{3}{2}}_{1} \\ &=\dfrac{1}{6}+\left(-\dfrac{9}{8}+\dfrac{4}{3}\right) \\ &=\dfrac{3}{8} \ \ \cdots \cdots \text{(答)}\end{align}$
※上記の解答例では$y$から積分を始めていますが、先に$x$で積分することも可能です。
(7)$\displaystyle \iiint_{D} z\ dxdydz$ $D:0 \leqq x \leqq 1$、$0 \leqq y \leqq 1-x$、$0 \leqq z \leqq 1-x-y$
$\begin{align}&\ \ \ \ \displaystyle \iiint_{D} z\ dxdydz \\ &=\displaystyle \int^{1}_{0} dx \int^{1-x}_{0} dy \int^{1-x-y}_{0} z\ dz \\ &=\displaystyle \int^{1}_{0} dx \int^{1-x}_{0} dy\ \left[\dfrac{1}{2}z^2\right]^{1-x-y}_{0} \\ &=\displaystyle \int^{1}_{0} dx \int^{1-x}_{0} \dfrac{1}{2}(1-x-y)^2\ dy \\ &=\displaystyle \int^{1}_{0} dx \int^{1-x}_{0} \dfrac{1}{2}(x+y-1)^2\ dy \\ &=\dfrac{1}{2}\int^{1}_{0}\left[\dfrac{1}{3}(x+y-1)^3\right]^{1-x}_{0}\ dx \\ &=\dfrac{1}{6}\int^{1}_{0}\{0-(x-1)^3\}\ dx \\ &=-\dfrac{1}{6}\int^{1}_{0}(x-1)^3\ dx \\ &=-\dfrac{1}{6}\left[\dfrac{1}{4}(x-1)^4\right]^{1}_{0} \\ &=-\dfrac{1}{24}(0-1) \\ &=\dfrac{1}{24} \ \ \cdots \cdots \text{(答)}\end{align}$
(8)$\displaystyle \iiint_{D} y\ dxdydz$ $D:x \geqq 0$、$y \geqq 0$、$z \geqq 0$、$x+2y+3z \leqq 6$
領域$D$は連立不等式$$\begin{cases} 0 \leqq x \leqq 6-3z-2y \\ 0 \leqq y \leqq \dfrac{3}{2}(2-z) \\ 0 \leqq z \leqq 2 \end{cases}$$によって表せるから、
$\begin{align}&\ \ \ \ \displaystyle \iiint_{D} y\ dxdydz \\ &=\displaystyle \int^{2}_{0}dz \int^{\frac{3}{2}(2-z)}_{0} dy \int^{6-3z-2y}_{0} y\ dx \\ &=\displaystyle \int^{2}_{0} dz \int^{\frac{3}{2}(2-z)}_{0}\ \big[xy\big]^{6-3z-2y}_{0}\ dy \\ &=\displaystyle \int^{2}_{0} dz \int^{\frac{3}{2}(2-z)}_{0} \{3(2-z)y-2y^2\}\ dy \\ &=\int^{2}_{0}\left[\dfrac{3}{2}(2-z)y^2-\dfrac{2}{3}y^3\right]^{\frac{3}{2}(2-z)}_{0}\ dz \\ &=\int^{2}_{0}\left\{\dfrac{27}{8}(2-z)^3-\dfrac{9}{4}(2-z)^3\right\}\ dz \\ &=\dfrac{9}{8}\int^{2}_{0}(2-z)^3\ dz \\ &=\dfrac{9}{8}\left[-\dfrac{1}{4}(2-z)^4\right]^{2}_{0} \\ &=-\dfrac{9}{32}(0-16) \\ &=\dfrac{9}{2} \ \ \cdots \cdots \text{(答)}\end{align}$
復習例題は設定していません。
