問題4.1.2
次の関数 $z=f(x,\ y)$ のグラフの$xz$平面、$yz$平面による切口の図形を描け。
（１） $z=\dfrac{x^2-y^2}{x^2+y^2} \ \ ((x,y) \ne (0,\ 0))$
（２） $z=\dfrac{x+y^3}{x^2+y^2} \ \ ((x,y) \ne (0,\ 0))$
《ポイント》
座標平面の意味を把握するところが初めの一歩です。例えば$xz$平面の場合、これは$$y=0$$という平面の方程式によって表すことができます。したがって、ある2変数関数 $z=f(x,\ y)$ のグラフの$xz$平面による切り口とは、$x$と$z$の2変数関数 $z=f(x,\ 0)$ に落とし込んだものと捉えることができます。そう考えれば、平面 $x=y$ による曲面の切り口も単なる代入計算によって求められることも理解できますね。
余談ではありますが「3D Graphing – GeoGebra」などの３D描画ソフトがウェブ上で無料で利用できますので、3次式プロットの具体的なイメージの湧かない方は一度使ってみると良いかもしれません。
《解答例》
（１）
$z=\dfrac{x^2-y^2}{x^2+y^2} \ \ ((x,y) \ne (0,\ 0))$
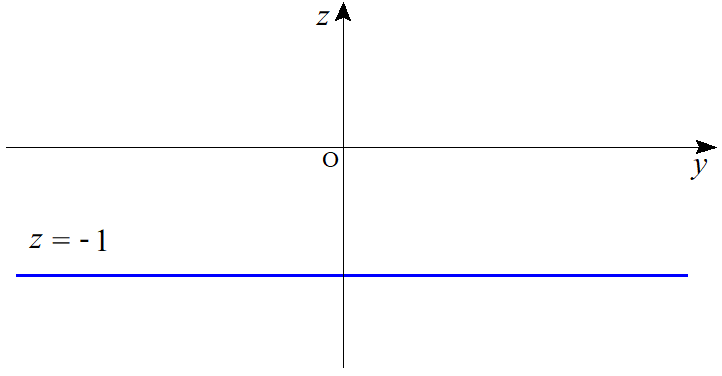
$xz$平面の方程式は $y=0$ であるから、$xz$平面による切口の図形の方程式は$$z=\dfrac{x^2-0^2}{x^2+0^2}$$ $$\therefore z=1$$となる。$yz$平面の方程式は $x=0$ であるから、$yz$平面による切口の図形の方程式は$$z=\dfrac{0^2-y^2}{0^2+y^2}$$ $$\therefore z=-1$$となる。したがって、それぞれ図示すると以下のようになる。
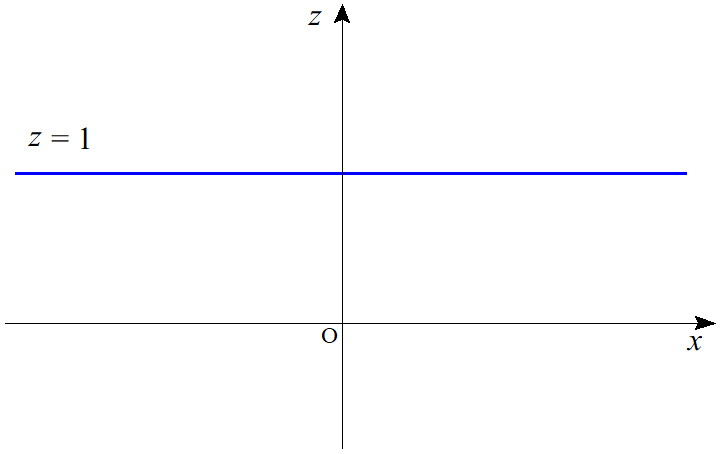$xz$平面による切口（但し $x \ne 0$）
$yz$平面による切口（但し $y \ne 0$）
（２）
$z=\dfrac{x+y^3}{x^2+y^2} \ \ ((x,y) \ne (0,\ 0))$
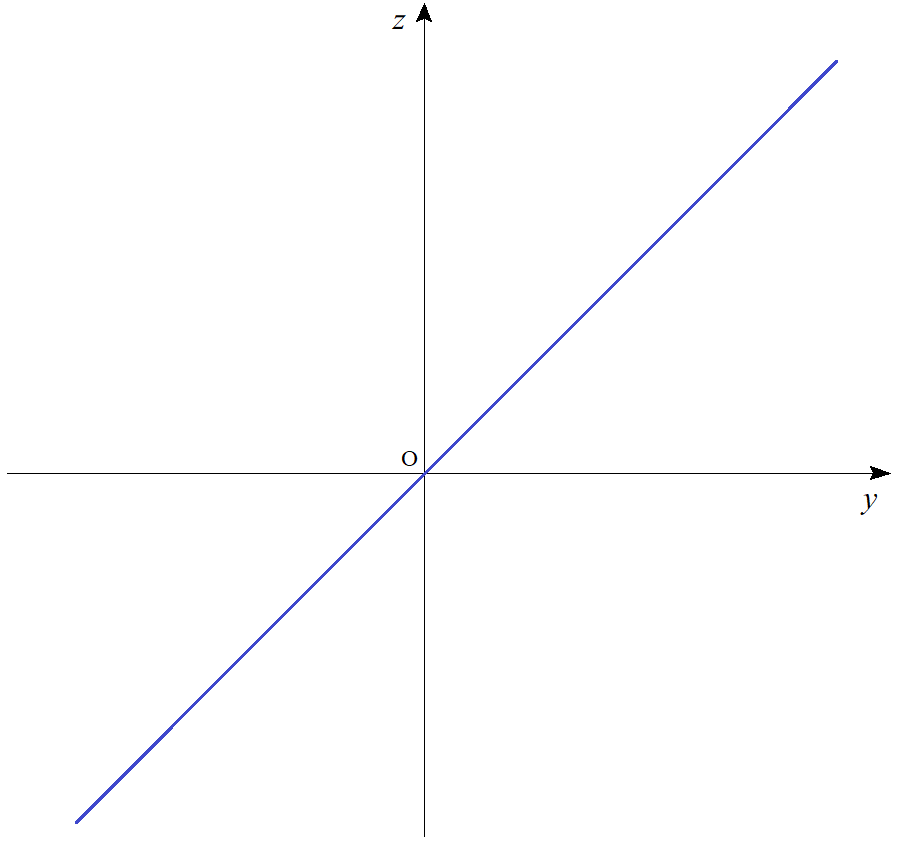
$xz$平面の方程式は $y=0$ であるから、$xz$平面による切口の図形の方程式は$$z=\dfrac{x+0^3}{x^2+0^2}$$ $$\therefore z=\dfrac{1}{x}$$となる。$yz$平面の方程式は $x=0$ であるから、$yz$平面による切口の図形の方程式は$$z=\dfrac{0+y^3}{0^2+y^2}$$ $$\therefore z=y$$となる。したがって、それぞれ図示すると以下のようになる。
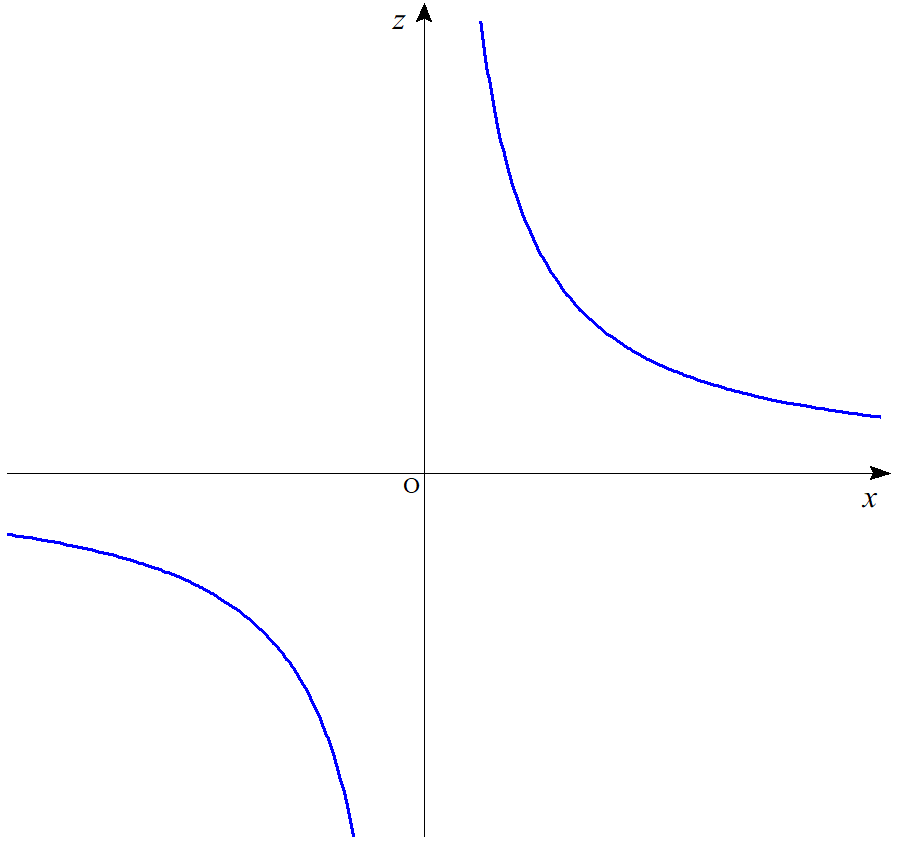$xz$平面による切口
$yz$平面による切口（但し $y \ne 0$）
復習例題は設定していません。