問題5.2.4
図(省略)のように極座標表示された曲線 $r=f(\theta)$($\alpha \leqq \theta \leqq \beta$)と $\theta=\alpha$、$\theta=\beta$ で囲まれる図形$D$の面積は$$S(D)=\dfrac{1}{2}\displaystyle \int^{\beta}_{\alpha}{f(\theta)}^2 d\theta$$であることを示し、次の曲線で囲まれる図形の面積を求めよ。
(1)$r=\sin \theta$
(2)$(x^2+y^2)^2=x^2-y^2$(レムニスケート)
(3)$r=a(1+\cos \theta)$($a>0$)(カーディオイド)
《ポイント》
以下に極座標における面積公式の略証を与えておきます。
$$\begin{align} S(D)&=\displaystyle \iint_D dxdy \\ &=\int^{\beta}_{\alpha} d\theta \int^{f(\theta)}_{0} r\ dr \\ &=\int^{\beta}_{\alpha} \dfrac{1}{2}{f(\theta)}^2 d\theta \end{align}$$ $$\therefore S(D)=\dfrac{1}{2}\displaystyle \int^{\beta}_{\alpha}{f(\theta)}^2 d\theta$$
また天下り的ではありますが、この公式は図形$D$内で微小角$\varDelta\theta$だけ動かしたときの図形を考えることでも得られます(下図)。
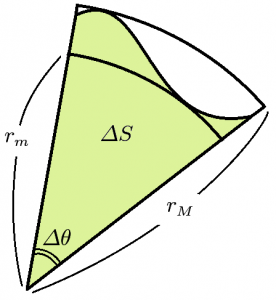
このとき$\varDelta\theta$の範囲において動径$f(\theta)$の最大値$r_M$、最小値$r_m$が定まり、$$r_m \leqq f(\theta) \leqq r_M$$となります。これより扇形の面積について不等関係$$\dfrac{1}{2}{r_m}^2 \varDelta\theta \leqq \varDelta S \leqq \dfrac{1}{2}{r_M}^2 \varDelta\theta$$が成り立ちます。極限 $\varDelta\theta \to 0$ を考えると $r_m \to f(\theta)$、$r_M \to f(\theta)$ となるので、$\alpha \to \beta$ の範囲で和をとると不等関係は以下のように書き直せます。$$\displaystyle \int^{\alpha}_{\beta} \dfrac{1}{2}{f(\theta)}^2 d\theta \leqq S(D) \leqq \int^{\alpha}_{\beta} \dfrac{1}{2}{f(\theta)}^2 d\theta$$これより$$S(D)=\dfrac{1}{2}\displaystyle \int^{\beta}_{\alpha}{f(\theta)}^2 d\theta$$を得ます。
《解答例》
(1)$r=\sin \theta$
$\begin{align}S&=\dfrac{1}{2}\displaystyle \int^{\pi}_{0}\sin^2 \theta\ d\theta \\ &= \int^{\frac{\pi}{2}}_{0}\sin^2 \theta\ d\theta \\ &=\dfrac{1}{2}\cdot\dfrac{\pi}{2} \\ &=\dfrac{\pi}{4} \ \ \cdots \cdots \text{(答)} \end{align}$
※この場合、動径が領域を1度だけ掃過するような$\theta$の範囲は $\pi \leqq \theta \leqq 0$ であることに注意しましょう。$\theta$が$\pi$を超えると動径が$2$周以上してしまいます。
(2)$(x^2+y^2)^2=x^2-y^2$(レムニスケート)
$x=r\cos \theta$、$y=r\sin \theta$ と置くと、$$(x^2+y^2)^2=x^2-y^2$$ $$\therefore r^4=r^2\cos^2 \theta-r^2\sin^2 \theta$$ $$\therefore r^2=\cos^2 \theta-\sin^2 \theta=\cos 2\theta$$となる。この曲線は$x$軸、$y$軸に関して対称であるから、$$S=4\cdot\dfrac{1}{2}\displaystyle \int^{\frac{\pi}{4}}_{0}\cos 2\theta\ d\theta$$となる。よって、
$\begin{align}S&=2\displaystyle \int^{\frac{\pi}{4}}_{0}\cos 2\theta\ d\theta \\ &=2\left[\dfrac{1}{2}\sin 2\theta \ \right]^{\frac{\pi}{4}}_{0} \\ &=1 \ \ \cdots \cdots \text{(答)} \end{align}$
(3)$r=a(1+\cos \theta)$($a>0$)(カーディオイド)
$\begin{align}S&=\dfrac{1}{2}\displaystyle \int^{2\pi}_{0}a^2(1+\cos \theta)^2\ d\theta \\ &=\displaystyle \dfrac{1}{2}a^2 \int^{2\pi}_{0}(1+2\cos \theta+\cos^2 \theta)\ d\theta \\ &=\displaystyle \dfrac{1}{2}a^2 \int^{2\pi}_{0}\left(1+2\cos \theta+\dfrac{1+\cos 2 \theta}{2}\right)\ d\theta \\ &=\dfrac{1}{2}a^2\left[\dfrac{3}{2}\theta +2\sin \theta +\dfrac{1}{4}\sin 2\theta \ \right]^{2\pi}_{0} \\ &=\dfrac{3\pi a^2}{2} \ \ \cdots \cdots \text{(答)} \end{align}$
復習例題は設定していません。
