問題5.4.1d
次の図形の体積を求めよ。
(5)曲面 $(x^2+y^2+z^2)^2=z$ で囲まれる図形
《ポイント》
空間内の図形$V$の体積$v(V)$は$$v(V)=\iiint_{V}dxdydz$$で与えられます。まずは空間内の図形を不等式で正しく定義する必要があります。図形の形によっては空間の極座標を利用した方が良いこともありますので、苦手な人はよく練習しておきましょう。
《解答例》
(5)曲面 $(x^2+y^2+z^2)^2=z$ で囲まれる図形
曲面 $(x^2+y^2+z^2)^2=z$ で囲まれる図形を$V$とし、$V$の体積を$v(V)$と置く。$x=r\sin \theta \cos \varphi$、$y=r\sin \theta \sin \varphi$、$z=r\cos \theta$ と置換すると、$$(x^2+y^2+z^2)^2=z$$ $$\therefore r^4=r\cos \theta$$ $$\therefore r^3=\cos \theta$$となる。また、$r$は負でない実数であるから、$0 \leqq \theta \leqq \dfrac{\pi}{2}$ が必要である。よって領域$W$を$W=\left\{(r,\theta,\varphi)\middle|\ 0 \leqq r \leqq \cos^{\frac{1}{3}} \theta ,\ 0 \leqq \theta \leqq \dfrac{\pi}{2} ,\ 0 \leqq \varphi < 2\pi \right\}$で定義すれば、$$\begin{align}v(V) &=\iiint_{V}dxdydz \\ &=\iiint_{W} r^2\sin\theta\ drd\theta d\varphi \\ &=\int^{2\pi}_{0}d\varphi \int^{\frac{\pi}{2}}_{0}d\theta \int^{\cos^{1/3} \theta }_{0}r^2\sin\theta\ dr \\ &=2\pi \int^{\frac{\pi}{2}}_{0} \left[\dfrac{r^3}{3}\sin\theta\right]^{\cos^{1/3} \theta}_{0} d\theta \\ &=\dfrac{2\pi}{3} \int^{\frac{\pi}{2}}_{0} \sin\theta\cos\theta\ d\theta \\ &=\dfrac{\pi}{3} \int^{\frac{\pi}{2}}_{0} \sin 2\theta\ d\theta \\ &=\dfrac{\pi}{3} \left[-\dfrac{1}{2}\cos 2\theta\right]^{\frac{\pi}{2}}_{0} \\ &=-\dfrac{\pi}{3} \cdot \dfrac{1}{2}(-1-1) \\ &=\dfrac{\pi}{3} \ \ \cdots \cdots \text{(答)} \end{align}$$と求められる。
※最後の積分は $\dfrac{1}{2}(\sin^2 \theta)^{\prime}=\sin\theta\cos\theta$ の関係を利用して$$\begin{align}\dfrac{2\pi}{3} \int^{\frac{\pi}{2}}_{0} \sin\theta\cos\theta\ d\theta &=\dfrac{2\pi}{3} \left[\dfrac{1}{2}\sin^2\theta\right]^{\frac{\pi}{2}}_{0} \\ &=\dfrac{\pi}{3}(1-0) \\ &=\dfrac{\pi}{3} \ \ \cdots \cdots \text{(答)} \end{align}$$と求めることもできます。
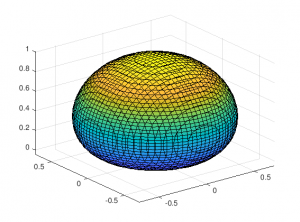
※本問の図形は$z$軸方向に球を潰した饅頭のような形の立体図形です。以下にMATLAB(マトラボ)によって出力した概形を示します。
入力は
f = @(x,y,z) ( x.^2 + y.^2 + z.^2 ).^2 - z; interval = [-1 1 -1 1 0 1]; fs = fimplicit3(f)
としています。
復習例題は設定していません。