問題2.4.5
次の関数が与えられた点で極値をとるかどうか、漸近展開を用いて調べよ。
(1)$f(x)=x^2 \sin x-x^3 e^x$
(2)$f(x)=x^2 \sin x-x \sin^{2}x$
(3)$f(x)=x^2-x^2 \cos x $
(4)$f(x)=(x-1)^2 \log x-(x-1)^3 \cos x $
《ポイント》
ランダウ記号を用いた極値判定では何次の項で括れるかによって答えが変わってきます。$x=0$での極値判定を例に取ってみましょう。
例えば、$f(x)-f(0)$が $x^4 \left(1+\dfrac{o(x^4 )}{x^4} \right)$、$x^3 \left(1+\dfrac{o(x^3 )}{x^3} \right)$とまとめられたとします。前者では4次の項で括れており、$x=0$付近で符号の変化がなく正なので$f(x)-f(0)>0$、即ち極小となると言えます。後者では3次の項で括れており$x=0$付近で符号が変化するため極値をとらないことが分かります。
つまり、極値を持つ関数は必ず偶数次数の項で括れなければいけません。問題を解く際にはこの点に注意しましょう。
《解答例》
(1)
$f(x)=x^2 \sin x-x^3 e^x$と置く。
$\begin{align}& \ \ \ \ \ f(x)-f(0) \\
&=x^2 \sin x-x^3 e^x \\
&=x^2 (x+o(x^2 ) )-x^3 (1+x+o(x)) \\
&=-x^4+x^2 \cdot o(x^2 )-x^3 \cdot o(x) \\
&=-x^4+o(x^4 )-o(x^4 ) \\
&=-x^4+o(x^4 ) \\
&=x^4 \left(-1+\dfrac{o(x^4 )}{x^4} \right) \end{align}$
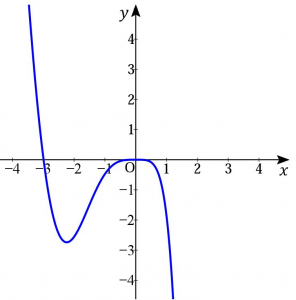
よって$x$が十分小さいときは負になるから、$f(x)<f(0)$である。よって$f(x)$は$x=0$で極大となる。
※$x=0$付近でのグラフは以下のようになる。
(2)
$f(x)=x^2 \sin x-x \sin^{2}x$と置く。
$\begin{align}& \ \ \ \ \ f(x)-f(0) \\
&=x^2 \sin x-x \sin^{2}x \\
&=x^2 \left(x-\dfrac{1}{3!} x^3+o(x^3 )\right)-x\left(x-\dfrac{1}{3!} x^3+o(x^3 )\right)^2 \\
&=\dfrac{1}{6} x^5+\left\{ -\dfrac{1}{36} x^7+\left( -\dfrac{1}{6} x^4+3x^2+x \cdot o(x^3 ) \right) \cdot o(x^3 ) \right\} \end{align}$
(∵中括弧内は5次以上)
$\begin{align}&=\dfrac{1}{6} x^5+o(x^5 ) \\
&=x^5 \left(\dfrac{1}{6}+\dfrac{o(x^5 )}{x^5} \right) \end{align}$
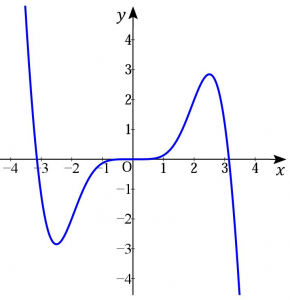
よって$x$が十分小さい正の実数であるときは$f(x)>f(0)$、一方$x$が十分小さい負の実数であるときは$f(x)<f(0)$である。よって$f(x)$は$x=0$で極値をとらない。
※$x=0$付近でのグラフは以下のようになる。
(3)
$f(x)=x^2-x^2 \cos x$と置く。
$\begin{align}& \ \ \ \ \ f(x)-f(0) \\
&=x^2-x^2 \cos x \\
&=x^2-x^2 \left( 1-\dfrac{1}{2!} x^2+o(x^2 ) \right) \\
&=\dfrac{1}{2} x^4+(-x^2) \cdot o(x^2 ) \\
&=\dfrac{1}{2} x^4+o(x^4 ) \\
&=x^4 \left( \dfrac{1}{2}+\dfrac{o(x^4 )}{x^4} \right) \end{align}$
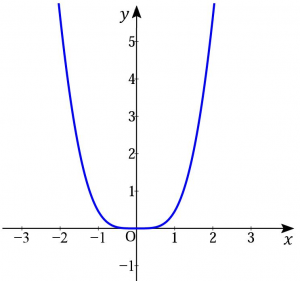
よって$x$が十分小さいときは正になるから、$f(x)>f(0)$である。よって$f(x)$は$x=0$で極小となる。
※$x=0$付近でのグラフは以下のようになる。
(4)
$x-1=t$と置き換え$g(t)=t^2 \log(t+1)-t^3$と置く。
$\begin{align}& \ \ \ \ \ g(t)-g(0) \\
&=t^2 \log(t+1)-t^3 \\
&=t^2 \left(t-\dfrac{1}{2} t^2+o(t^2 ) \right)-t^3 \\
&=-\dfrac{1}{2} t^4+t^2 \cdot o(t^2 ) \\
&=-\dfrac{1}{2} t^4+o(t^4 ) \\
&=t^4 \left(-\dfrac{1}{2}+\dfrac{o(t^4 )}{t^4} \right) \end{align}$
よって$t$が十分小さいときは負になるから、$g(t)<g(0)$である。よって$g(t)$は$t=0$で極大となる。故に$f(x)$は$x=1$で極大となる。
※$x=1$付近での$f(x)$のグラフは以下のようになる。($x \to +0$ のとき$y$軸に漸近する)
《コメント》
(4)では$x-1=t$と置き換えていますが、これは$x \to 1$を$t \to 0$に読み替えてランダウの記号を使いやすくするためです。ランダウの記号については当サイトの記事「ランダウの記号と漸近展開の2通りの求め方(漸近展開の合成)」で解説しています。
復習例題未設定