問題3.4.3
次の曲線と$x$軸で囲まれる図形の面積を求めよ。
(1) $\begin{cases} x=2t+1 \\ y=2-t-t^2 \end{cases}$
(2) $\begin{cases} x=\sin t \\ y=t \cos t \end{cases} \ \ \ \left(0 \le t \le \dfrac{\pi}{2}\right)$
(3) $\begin{cases} x=a(t-\sin t) \\ y=a(1-\cos t) \end{cases} \ \ \ (a>0,\ 0 \le t \le 2\pi)$
《ポイント》
関数が $y=f(x)$ という形(陽関数)の場合、面積は定積分$$\displaystyle \int_{a}^{b} f(x)dx$$によって求めることができます。パラメータ表示された曲線の場合は積分変数を媒介変数に直して処理することになります。滑らかな曲線$C$が $\begin{cases} x=X(t) \\ y=Y(t) \ \ \ (a \leqq t \leqq b)\end{cases}$ で与えられるとき、面積は定積分$$\displaystyle \int_{X(a)}^{X(b)} y\dfrac{dx}{dt}\ dt$$により求められます。
前問同様、パラメータ表示された曲線は形状がイメージしにくいので増減表を書くと良いでしょう。また、曲線$C$の媒介変数が消去できる場合は陽関数に書き直してから積分しても構いません。
《解答例》
(1)
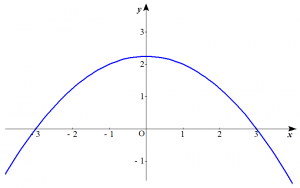
曲線$C$:$\begin{cases} x=2t+1 \\ y=2-t-t^2 \end{cases}$ とする。
$x$は単調増加であり、$y$は $t=1,-2$ で$0$となる。また、$\dfrac{dx}{dt}=2$、$\dfrac{dy}{dt}=-1-2t$ であるから増減表は以下のようになる。
| $t$ | ・・・ | $-2$ | ・・・ | $\dfrac{1}{2}$ | ・・・ | $1$ | ・・・ |
| $x^{\prime}$ | + | + | + | + | + | + | + |
| $y^{\prime}$ | + | + | + | $0$ | – | – | – |
| $x$ | $\nearrow$ | $-3$ | $\nearrow$ | $0$ | $\nearrow$ | $3$ | $\nearrow$ |
| $y$ | $\nearrow$ | $0$ | $\nearrow$ | $\dfrac{9}{4}$ | $\searrow$ | $0$ | $\searrow$ |
よって求める図形の面積を$S$とすると、
$\begin{align}&S = \displaystyle \int_{-3}^{3} ydx \\
&= \displaystyle \int_{-2}^{1} y\dfrac{dx}{dt}dt \\
&= \displaystyle \int_{-2}^{1} (2-t-t^2)\cdot 2\ dt \\
&=2\left[2t-\dfrac{1}{2}t^2-\dfrac{1}{3}t^3\right]_{-2}^{1} \\
&=9 \ \ \cdots \cdots \text{(答)} \end{align}$
《別解》:$t$を消去する
$t=\dfrac{x-1}{2}$ より、$$y=2-\dfrac{x-1}{2}-\dfrac{(x-1)^2}{4}$$ $$\therefore y=-\dfrac{1}{4}x^2+\dfrac{9}{4}$$となる。これは$y$軸に関して対称であるから、求める図形の面積を$S$とすると、
$\begin{align}&S = \displaystyle \int_{-3}^{3} ydx \\
&= \displaystyle \int_{-3}^{3} -\dfrac{1}{4}(x^2-9)dx \\
&= -\dfrac{1}{2}\displaystyle \int_{0}^{3} (x^2-9)dx \\
&=-\dfrac{1}{2}\left[\dfrac{1}{3}x^3-9x\right]_{-3}^{3} \\
&=9 \ \ \cdots \cdots \text{(答)} \end{align}$
※曲線$C$:$\begin{cases} x=2t+1 \\ y=2-t-t^2 \end{cases}$ は以下のような放物線です。
(2)
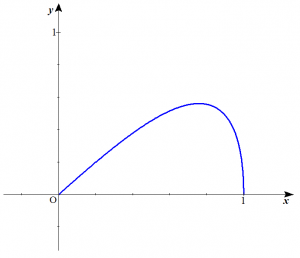
曲線$C$:$\begin{cases} x=\sin t \\ y=t \cos t \end{cases} \ \ \ \left(0 \le t \le \dfrac{\pi}{2}\right)$ とする。
$y$は $t=0,\ \dfrac{\pi}{2}$ で$0$となり、$\dfrac{dx}{dt}=\cos t$、$\dfrac{dy}{dt}=\cos t-t\sin t$ であるから増減表は以下のようになる。
| $t$ | $0$ | ・・・ | $\alpha$ | ・・・ | $\dfrac{\pi}{2}$ |
| $\dfrac{dy}{dx}$ | $(1)$ | + | $0$ | – | $(\infty)$ |
| $x$ | $0$ | $\nearrow$ | $\nearrow$ | $1$ | |
| $y$ | $0$ | $\nearrow$ | $\searrow$ | $0$ |
(ここで$\alpha$は $\alpha=\dfrac{1}{\tan \alpha}$ かつ $0<\alpha<\dfrac{\pi}{2}$ を満たす実数である)
これより求める図形の面積を$S$とすると、
$\begin{align}&S = \displaystyle \int_{0}^{1} y\ dx \\
&= \displaystyle \int_{0}^{\frac{\pi}{2}} y\dfrac{dx}{dt}dt \\
&= \displaystyle \int_{0}^{\frac{\pi}{2}} t \cos^2 t\ dt \\
&= \displaystyle \int_{0}^{\frac{\pi}{2}} t \cdot \dfrac{1+\cos 2t}{2} dt \\
&= \displaystyle \dfrac{1}{2}\int_{0}^{\frac{\pi}{2}} (t+t\cos 2t) dt \\
&=\dfrac{1}{2}\left[\dfrac{1}{2}t^2\right]_{0}^{\frac{\pi}{2}}+\dfrac{1}{2}\left[t\cdot\dfrac{1}{2}\sin 2t\right]_{0}^{\frac{\pi}{2}}-\dfrac{1}{2}\int_{0}^{\frac{\pi}{2}} \dfrac{1}{2}\sin 2t\ dt \\
&=\dfrac{\pi^2}{16}+0-\dfrac{1}{4}\left[-\dfrac{1}{2} \cos 2t\right]_{0}^{\frac{\pi}{2}} \\
&=\dfrac{\pi^2}{16}+\dfrac{1}{8}(-1-1) \\
&=\dfrac{\pi^2}{16}-\dfrac{1}{4} \ \ \cdots \cdots \text{(答)} \end{align}$
※曲線$C$:$\begin{cases} x=\sin t \\ y=t \cos t \end{cases} \ \ \ \left(0 \le t \le \dfrac{\pi}{2}\right)$ は以下のような曲線です($t$の範囲を広げれば原点に関して対称な曲線であることが分かります)。
(3)
曲線$C$:$\begin{cases} x=a(t-\sin t) \\ y=a(1-\cos t) \end{cases} \ \ \ (a>0,\ 0 \le t \le 2\pi)$ とする。
$y$は $t=0,\ 2\pi$ で$0$となり、$\dfrac{dx}{dt}=a(1-\cos t)$、$\dfrac{dy}{dt}=a\sin t$ であるから$$\begin{align}\dfrac{dy}{dx}&=\dfrac{\sin t}{1-\cos t}\\ &=\dfrac{\sin t(1+\cos t)}{1-\cos^2 t} \\ &=\dfrac{1+\cos t}{\sin t} \end{align}$$となる。よって増減表は以下のようになる。
| $t$ | $0$ | ・・・ | $\pi$ | ・・・ | $2\pi$ |
| $\dfrac{dy}{dx}$ | $(\infty)$ | + | $0$ | – | $(-\infty)$ |
| $x$ | $0$ | $\nearrow$ | $\pi a$ | $\nearrow$ | $2\pi a$ |
| $y$ | $0$ | $\nearrow$ | $2a$ | $\searrow$ | $0$ |
これより求める図形の面積を$S$とすると、
$\begin{align}&S = \displaystyle \int_{0}^{2\pi a} y\ dx \\
&= \displaystyle \int_{0}^{2\pi} y\dfrac{dx}{dt}dt \\
&= \displaystyle \int_{0}^{2\pi} a^2 (1-\cos t)^2 dt \\
&= \displaystyle a^2\int_{0}^{2\pi} (1-2\cos t+\cos^2 t) dt \\
&= \displaystyle a^2\int_{0}^{2\pi} (1+\cos^2 t) dt \ \ \ \left(\because \int_{0}^{2\pi} \cos t dt =0\right)\\
&= \displaystyle a^2\int_{0}^{2\pi} \left(1+\dfrac{1+\cos 2t}{2}\right) dt \\
&= \displaystyle \dfrac{a^2}{2}\int_{0}^{2\pi} (3+\cos 2t) dt \\
&=\dfrac{a^2}{2}\left[3t+\dfrac{1}{2}\sin 2t \right]_{0}^{2\pi} \\
&=\dfrac{a^2}{2}(6\pi-0) \\
&=3\pi a^2 \ \ \cdots \cdots \text{(答)} \end{align}$
《別解》:倍角の公式を利用する
$\begin{align}S &= \displaystyle \int_{0}^{2\pi a} y\ dx \\
&= \displaystyle \int_{0}^{2\pi} y\dfrac{dx}{dt}dt \\
&= \displaystyle \int_{0}^{2\pi} a^2 (1-\cos t)^2 dt \\
&= \displaystyle a^2\int_{0}^{2\pi} \left\{1-\left(1-2\sin^2 \dfrac{t}{2}\right)\right\}^2 dt \\
&= \displaystyle 4a^2\int_{0}^{2\pi} \sin^4 \dfrac{t}{2} dt \ \ \cdots \cdots (*) \end{align}$
ここで $u=\dfrac{t}{2}$ と置くと、$dt=2du$ であり、$t:0 \to 2\pi$ のとき $u:0 \to \pi$
$\begin{align}(*)&= \displaystyle 4a^2\int_{0}^{\pi} \sin^4 u \cdot 2du \\
&= \displaystyle 8a^2\int_{0}^{\frac{\pi}{2}} 2\sin^4 u du \\
&= \displaystyle 16a^2\int_{0}^{\frac{\pi}{2}} \sin^4 u du \\
&=16a^2 \cdot \dfrac{3!!}{4!!} \cdot \dfrac{\pi}{2} \\
&=3\pi a^2 \ \ \cdots \cdots \text{(答)} \end{align}$
※ウォリスの公式より$$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^4 u du=\dfrac{3!!}{4!!} \cdot \dfrac{\pi}{2}=\dfrac{3}{4} \cdot \dfrac{1}{2} \cdot \dfrac{\pi}{2}$$となります。
※曲線$C$:$\begin{cases} x=a(t-\sin t) \\ y=a(1-\cos t) \end{cases} \ \ \ (a>0,\ 0 \le t \le 2\pi)$ はサイクロイドです。
復習例題未設定