問題5.1.3
積分の順序を変更せよ
(1)$\displaystyle \int^{1}_{-1}dx \int^{2\sqrt{1-x^2}}_{0} f(x,y)\ dy$
(2)$\displaystyle \int^{1}_{-2}dx \int^{-x+2}_{x^2} f(x,y)\ dy$
(3)$\displaystyle \int^{4}_{0}dy \int^{2\sqrt{y}}_{y} f(x,y)\ dx$
(4)$\displaystyle \int^{4}_{0}dy \int^{\sqrt{y}}_{y-2} f(x,y)\ dx$
《ポイント》
累次積分の積分の順序を入れ替える際は領域の形状によく注意するべきでしょう。境界となっている曲線の逆関数が簡単に表示できない場合は領域を一度図示してみるのも手です。
《解答例》
(1)$\displaystyle \int^{1}_{-1}dx \int^{2\sqrt{1-x^2}}_{0} f(x,y)\ dy$
$y=2\sqrt{1-x^2}$ を$x$について解くと$$x=\pm\dfrac{\sqrt{4-y^2}}{2}$$となるから、$x:-1 \to 1$ のとき $y:0 \to 2$ である。よって、
$\begin{align}&\ \ \ \ \displaystyle \int^{1}_{-1}dx \int^{2\sqrt{1-x^2}}_{0} f(x,y)\ dy \\ &=\displaystyle \int^{2}_{0}dy \int^{\frac{\sqrt{4-y^2}}{2}}_{-\frac{\sqrt{4-y^2}}{2}} f(x,y)\ dx \ \ \cdots \cdots \text{(答)}\end{align}$
となる。
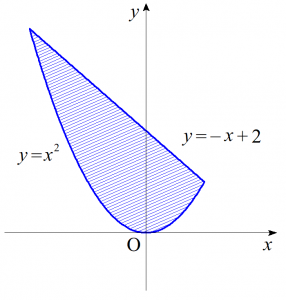
(2)$\displaystyle \int^{1}_{-2}dx \int^{-x+2}_{x^2} f(x,y)\ dy$
積分領域を図示すると以下のようになる。
よって、
$\begin{align}&\ \ \ \ \displaystyle \int^{1}_{-2}dx \int^{-x+2}_{x^2} f(x,y)\ dy \\ &=\displaystyle \int^{1}_{0}dy \int^{\sqrt{y}}_{-\sqrt{y}} f(x,y)\ dx + \int^{4}_{1}dy \int^{2-y}_{-\sqrt{y}} f(x,y)\ dx \ \ \cdots \cdots \text{(答)}\end{align}$
となる。
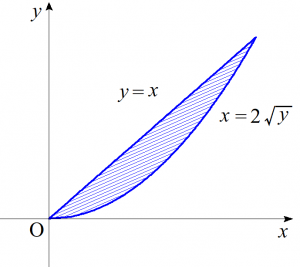
(3)$\displaystyle \int^{4}_{0}dy \int^{2\sqrt{y}}_{y} f(x,y)\ dx$
積分領域を図示すると以下のようになる。
よって
$\begin{align}&\ \ \ \ \displaystyle \int^{4}_{0}dy \int^{2\sqrt{y}}_{y} f(x,y)\ dx \\ &=\displaystyle \int^{4}_{0}dx \int^{x}_{\frac{x^2}{4}} f(x,y)\ dy \ \ \cdots \cdots \text{(答)}\end{align}$
となる。
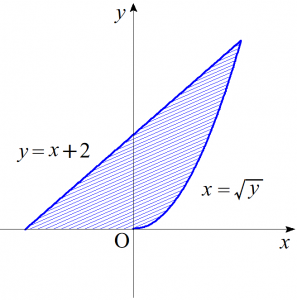
(4)$\displaystyle \int^{4}_{0}dy \int^{\sqrt{y}}_{y-2} f(x,y)\ dx$
積分領域を図示すると以下のようになる。
よって
$\begin{align}&\ \ \ \ \displaystyle \int^{4}_{0}dy \int^{\sqrt{y}}_{y-2} f(x,y)\ dx \\ &=\displaystyle \int^{0}_{-2}dx \int^{x+2}_{0} f(x,y)\ dy + \int^{2}_{0}dx \int^{x+2}_{x^2} f(x,y)\ dy \ \ \cdots \cdots \text{(答)}\end{align}$
となる。
復習例題は設定していません。