問題5.4.4a
次の図形の曲面積を求めよ（$a>0$）。
（１）円柱 $y^2+z^2=a^2$ の円柱 $x^2+y^2=a^2$ の内部にある部分
（２）円柱 $y^2+z^2=a^2$ の球 $x^2+y^2+z^2=2a^2$ の内部にある部分
《ポイント》
いきなり曲面の立体的なイメージを思い描くのではなく、まずは不等式を用いて数式のとりうる値の範囲を求めましょう。積分する方向によって積分計算のしやすさが変わってくるので積分する文字や順序に注意しなければなりません。
《解答例》
（１）円柱 $y^2+z^2=a^2$ の円柱 $x^2+y^2=a^2$ の内部にある部分
$y^2+z^2=a^2$ を$z$に関して解くと、$$z=\pm\sqrt{a^2-y^2}$$となる。このうち円柱 $x^2+y^2=a^2$ の内部にある部分を$K$とする。２つの円柱は$xy$平面に関して対称なので、$z \geqq 0$ の部分$K^+$の曲面積を２倍すればよい。同様に、$K^+$は$yz$平面、$xz$平面に関して対称なので、結局$K$の曲面積を求めるには $x \geqq 0$ かつ $y \geqq 0$ かつ $z \geqq 0$ の部分$K^{\prime}$の曲面積を８倍すればよいことになる。そこで領域$D$を$$D=\left\{(x,y)\middle|\ x^2+y^2 \leqq a^2,x \geqq 0,y \geqq 0\right\}$$によって定めれば、求める$K$の曲面積$S(K)$は$$\begin{align}S(K)&=8\iint_D\sqrt{1+{z_x}^2+{z_y}^2}\ dxdy \\ &=8\iint_D\sqrt{1+0+\left(\dfrac{-y}{\sqrt{a^2-y^2}}\right)^2}\ dxdy \\ &=8a\iint_D\dfrac{1}{\sqrt{a^2-y^2}}\ dxdy \\ &=8a\int^{a}_{0} dy \int^{\sqrt{a^2-y^2}}_{0}\dfrac{1}{\sqrt{a^2-y^2}}dx \\ &=8a\int^{a}_{0} \left[\dfrac{x}{\sqrt{a^2-y^2}}\right]^{\sqrt{a^2-y^2}}_{0}dy \\ \\ &=8a\int^{a}_{0} dy \\ &=8a^2 \ \ \cdots \cdots \text{(答)} \end{align}$$と求められる。
（２）円柱 $y^2+z^2=a^2$ の球 $x^2+y^2+z^2=2a^2$ の内部にある部分
$y^2+z^2=a^2$ を$z$に関して解くと、$$z=\pm\sqrt{a^2-y^2}$$となる。これは$xy$平面に関して対称であるから、$z \geqq 0$ の曲面積を２倍すればよい。
$y^2+z^2=a^2$ と $x^2+y^2+z^2=2a^2$ を連立すると$$x^2=a^2$$を得る。$a>0$ より$$x=\pm a$$となるので、円柱 $y^2+z^2=a^2$ の球 $x^2+y^2+z^2=2a^2$ の内部にある部分は$$|x| \leqq a$$を満たす。円柱と球の共有点は $x^2=a^2$ を満たす曲線上にしか存在しないから、新たに領域$D$を$$D=\left\{(x,y)\middle|\ |x| \leqq a\right\}$$によって定めれば、求める曲面積$S$は$$\begin{align}S&=2\iint_D\sqrt{1+{z_x}^2+{z_y}^2}\ dxdy \\ &=2\iint_D\sqrt{1+0+\left(\dfrac{-y}{\sqrt{a^2-y^2}}\right)^2}\ dxdy \\ &=2a\iint_D\dfrac{1}{\sqrt{a^2-y^2}}\ dxdy \\ &=2a\int^{a}_{-a} dy \int^{a}_{-a}\dfrac{1}{\sqrt{a^2-y^2}}dx \\ &=2a\int^{a}_{0} \left[\dfrac{x}{\sqrt{a^2-y^2}}\right]^{a}_{-a}dy \\ &=4a^2\int^{a}_{-a}\dfrac{1}{\sqrt{a^2-y^2}} dy \\ &=4a^2 \left[\sin^{-1}\dfrac{y}{a}\right]^{a}_{-a} \\ &=4a^2\left\{\dfrac{\pi}{2}-\left(-\dfrac{\pi}{2}\right)\right\} \\ &=4\pi a^2 \ \ \cdots \cdots \text{(答)} \end{align}$$と求められる。
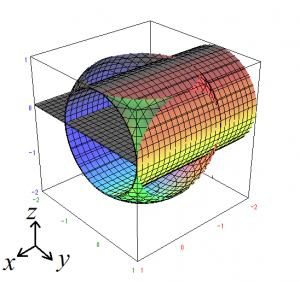
※題意の立体図形を $a=1$ としてプロットすると以下のようになります。灰色の面が$xy$平面（z=0）で、プロットの範囲は $-2 \leqq x,y,z \leqq 1$ としています（わざと球がくりぬかれるようにプロットしています）。
3D plot by “GCalc-Plus”この図から、手前の断面（$x=1$）で円柱 $y^2+z^2=a^2$ と球 $x^2+y^2+z^2=2a^2$ がぴったり交差しているのが分かります。交差する部分は平面 $x=a$ と $x=-a$ のみなので、実は求めるべき曲面積は円柱の側面積に一致します。これにより、$$S=2a \times 2\pi a=4\pi a^2$$と瞬時に求めることができてしまいます（本問の円柱の高さは$2a$、円周は$2\pi a$です）。
復習例題は設定していません。