問題2.2.3
次の関数の増減と極値を調べ、グラフの概形を描け。
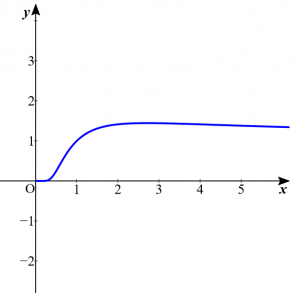
(1)$y=x^{\frac{1}{x}}$
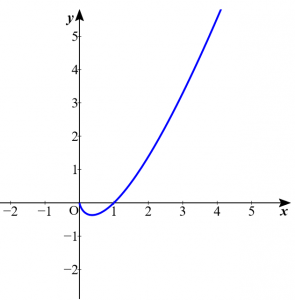
(2)$y=x \log x$
《ポイント》
関数の形に応じて対数微分法の利用やロピタルの定理の利用を考えましょう。
《解答例》
(1)
$y=x^{\frac{1}{x}}$とし、両辺に自然対数を取ると、
$\log y=\dfrac{\log x}{x}$となる。両辺を$x$について微分すると
$y’=x^{\frac{1}{x}} \cdot \dfrac{1-\log x}{x^2}$を得る。また、$\displaystyle \lim_{x \to +0} \dfrac{\log x}{x}=-\infty$が成り立つから、$x \to +0$のとき$y \to +0$である。以上より増減表は以下のようになる。
$$\begin{array}{|c|c|c|c|c|c|}
\hline x & (0) & \cdots & e & \cdots & (\infty) \\
\hline y^{\prime} & & + & 0 & – & \\
\hline y & (0) & \nearrow & e^{\frac{1}{e}} & \searrow & (0) \\
\hline
\end{array}$$
表より、グラフは以下のようになる。
(2)
$y=x \log x \ \ (x>0)$とし、両辺を$x$について微分すると
$y’=\log x+1$を得る。また、ロピタルの定理より、
$\begin{align} \displaystyle \lim_{x \to +0} x \log x &=\lim_{x \to +0} \dfrac{\log x}{\dfrac{1}{x}} \\ &=\lim_{x \to +0} \dfrac{\dfrac{1}{x}}{-\left( \dfrac{1}{x} \right)^2} \\ &=\lim_{x \to +0} (-x) \\ &=-0 \end{align}$
となる。よって増減表は以下。
$$\begin{array}{|c|c|c|c|c|c|}
\hline x & (0) & \cdots & \frac{1}{e} & \cdots & (\infty) \\
\hline y^{\prime} & & – & 0 & + & \\
\hline y & (0) & \searrow & -\frac{1}{e} & \nearrow & (\infty) \\
\hline
\end{array}$$
表より、グラフは以下のようになる。
《コメント》
関数のグラフを描くときは端点が発散するのか、収束するのかをしっかり調べましょう。その際に便利なのがロピタルの定理ですが、利用可能な条件があるので注意しましょう(次頁で詳しく扱います)。
復習例題未設定