指数関数$k^n$の各桁の数の総和
整数$n$の各桁の数の総和を与える関数を$d(n)$と置くことにします。例えば $2^{10}=1024$ なので $d(2^{10})=7$ となります。下図は$d(k)$~$d(k^{100})$の各位の数の総和を $k=1,2,\cdots ,9$ についてプロットしたもので、横軸が$n$、縦軸が$d(k^n)$です。
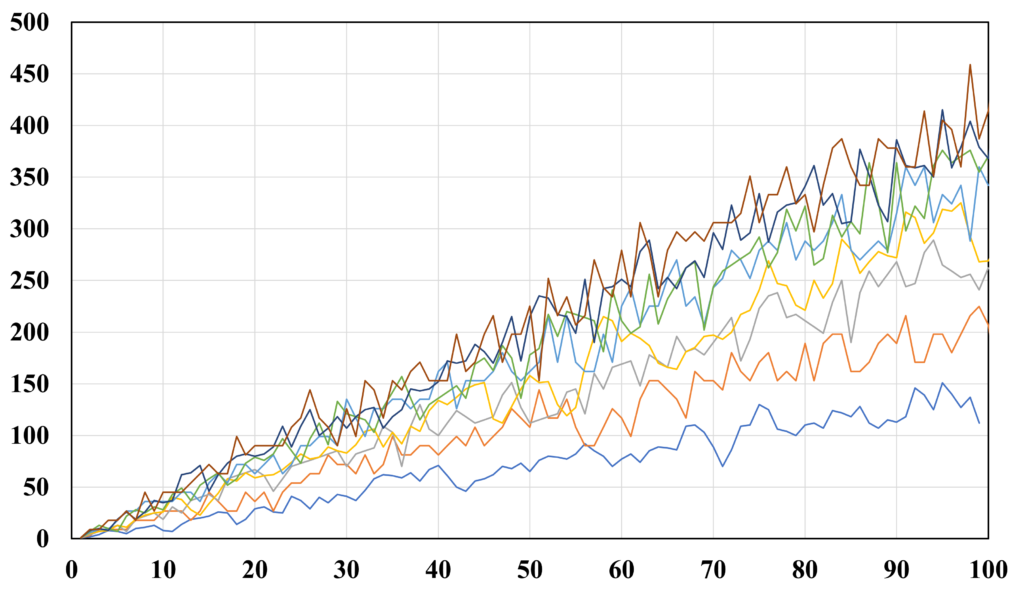
$n=100$ までのリストを以下に示します。
| $n$ | $2^n$ | $3^n$ | $4^n$ | $5^n$ | $6^n$ | $7^n$ | $8^n$ | $9^n$ |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 4 | 9 | 7 | 7 | 9 | 13 | 10 | 9 |
| 3 | 8 | 9 | 10 | 8 | 9 | 10 | 8 | 18 |
| 4 | 7 | 9 | 13 | 13 | 18 | 7 | 19 | 18 |
| 5 | 5 | 9 | 7 | 11 | 27 | 22 | 26 | 27 |
| 6 | 10 | 18 | 19 | 19 | 27 | 28 | 19 | 18 |
| 7 | 11 | 18 | 22 | 23 | 36 | 25 | 26 | 45 |
| 8 | 13 | 18 | 25 | 25 | 36 | 31 | 37 | 27 |
| 9 | 8 | 27 | 19 | 26 | 36 | 28 | 35 | 45 |
| 10 | 7 | 27 | 31 | 40 | 36 | 43 | 37 | 45 |
| 11 | 14 | 27 | 25 | 38 | 45 | 49 | 62 | 45 |
| 12 | 19 | 18 | 37 | 28 | 45 | 37 | 64 | 54 |
| 13 | 20 | 27 | 40 | 23 | 36 | 52 | 71 | 63 |
| 14 | 22 | 45 | 43 | 34 | 54 | 58 | 46 | 72 |
| 15 | 26 | 36 | 37 | 44 | 63 | 64 | 62 | 63 |
| 16 | 25 | 27 | 58 | 58 | 54 | 52 | 73 | 63 |
| 17 | 14 | 27 | 61 | 56 | 72 | 58 | 80 | 99 |
| 18 | 19 | 45 | 64 | 64 | 72 | 73 | 82 | 81 |
| 19 | 29 | 36 | 67 | 59 | 63 | 79 | 80 | 90 |
| 20 | 31 | 45 | 61 | 61 | 72 | 76 | 82 | 90 |
| 21 | 26 | 27 | 46 | 62 | 81 | 82 | 89 | 90 |
| 22 | 25 | 45 | 58 | 67 | 63 | 97 | 109 | 90 |
| 23 | 41 | 54 | 70 | 74 | 72 | 85 | 89 | 108 |
| 24 | 37 | 54 | 73 | 82 | 90 | 73 | 109 | 117 |
| 25 | 29 | 63 | 76 | 77 | 90 | 97 | 125 | 144 |
| 26 | 40 | 63 | 79 | 79 | 99 | 112 | 100 | 117 |
| 27 | 35 | 81 | 82 | 89 | 99 | 91 | 107 | 108 |
| 28 | 43 | 72 | 85 | 85 | 90 | 133 | 118 | 90 |
| 29 | 41 | 72 | 70 | 83 | 135 | 121 | 107 | 126 |
| 30 | 37 | 63 | 82 | 91 | 117 | 118 | 118 | 99 |
| 31 | 47 | 81 | 85 | 104 | 99 | 115 | 125 | 153 |
| 32 | 58 | 63 | 88 | 106 | 126 | 103 | 127 | 144 |
| 33 | 62 | 72 | 109 | 89 | 126 | 127 | 107 | 117 |
| 34 | 61 | 99 | 103 | 103 | 135 | 142 | 118 | 153 |
| 35 | 59 | 81 | 70 | 92 | 135 | 157 | 125 | 144 |
| 36 | 64 | 81 | 109 | 109 | 126 | 136 | 145 | 162 |
| 37 | 56 | 90 | 130 | 104 | 135 | 115 | 143 | 171 |
| 38 | 67 | 90 | 106 | 124 | 135 | 130 | 145 | 153 |
| 39 | 71 | 81 | 100 | 134 | 162 | 136 | 152 | 153 |
| 40 | 61 | 90 | 112 | 130 | 171 | 142 | 172 | 153 |
| 41 | 50 | 99 | 124 | 137 | 126 | 148 | 170 | 198 |
| 42 | 46 | 90 | 118 | 145 | 153 | 136 | 172 | 162 |
| 43 | 56 | 108 | 112 | 149 | 153 | 169 | 188 | 171 |
| 44 | 58 | 90 | 115 | 151 | 153 | 175 | 181 | 198 |
| 45 | 62 | 99 | 118 | 116 | 162 | 163 | 170 | 216 |
| 46 | 70 | 108 | 139 | 112 | 180 | 187 | 190 | 171 |
| 47 | 68 | 126 | 151 | 128 | 162 | 175 | 215 | 198 |
| 48 | 73 | 117 | 127 | 145 | 153 | 136 | 172 | 198 |
| 49 | 65 | 108 | 112 | 158 | 162 | 178 | 215 | 225 |
| 50 | 76 | 144 | 115 | 151 | 171 | 184 | 235 | 153 |
| 51 | 80 | 117 | 118 | 152 | 216 | 217 | 233 | 252 |
| 52 | 79 | 117 | 121 | 130 | 171 | 196 | 217 | 216 |
| 53 | 77 | 135 | 142 | 119 | 216 | 220 | 215 | 234 |
| 54 | 82 | 108 | 145 | 127 | 171 | 217 | 199 | 207 |
| 55 | 92 | 90 | 121 | 167 | 162 | 214 | 251 | 216 |
| 56 | 85 | 90 | 160 | 196 | 162 | 211 | 190 | 270 |
| 57 | 80 | 108 | 145 | 215 | 198 | 181 | 242 | 243 |
| 58 | 70 | 126 | 166 | 211 | 171 | 241 | 244 | 234 |
| 59 | 77 | 117 | 169 | 191 | 225 | 211 | 251 | 279 |
| 60 | 82 | 99 | 172 | 199 | 243 | 199 | 244 | 234 |
| 61 | 74 | 135 | 148 | 194 | 207 | 205 | 278 | 306 |
| 62 | 85 | 153 | 178 | 187 | 225 | 256 | 289 | 279 |
| 63 | 89 | 153 | 172 | 170 | 225 | 208 | 242 | 234 |
| 64 | 88 | 144 | 166 | 166 | 252 | 232 | 253 | 279 |
| 65 | 86 | 135 | 196 | 164 | 270 | 247 | 242 | 297 |
| 66 | 109 | 117 | 181 | 181 | 225 | 262 | 262 | 288 |
| 67 | 110 | 162 | 184 | 185 | 234 | 268 | 269 | 297 |
| 68 | 103 | 153 | 178 | 196 | 207 | 202 | 253 | 288 |
| 69 | 89 | 153 | 190 | 197 | 243 | 244 | 296 | 306 |
| 70 | 70 | 144 | 202 | 193 | 252 | 259 | 280 | 306 |
| 71 | 86 | 180 | 214 | 200 | 279 | 265 | 323 | 306 |
| 72 | 109 | 162 | 172 | 217 | 270 | 271 | 289 | 315 |
| 73 | 110 | 153 | 193 | 221 | 252 | 277 | 296 | 351 |
| 74 | 130 | 171 | 223 | 241 | 279 | 292 | 334 | 306 |
| 75 | 125 | 180 | 235 | 269 | 288 | 262 | 287 | 333 |
| 76 | 106 | 153 | 238 | 247 | 279 | 277 | 316 | 333 |
| 77 | 104 | 162 | 214 | 245 | 306 | 319 | 323 | 360 |
| 78 | 100 | 153 | 217 | 226 | 270 | 298 | 325 | 324 |
| 79 | 110 | 189 | 211 | 221 | 288 | 322 | 341 | 333 |
| 80 | 112 | 153 | 205 | 250 | 279 | 265 | 361 | 297 |
| 81 | 107 | 189 | 199 | 233 | 288 | 271 | 323 | 342 |
| 82 | 124 | 198 | 229 | 247 | 306 | 313 | 334 | 378 |
| 83 | 122 | 198 | 250 | 290 | 333 | 292 | 305 | 387 |
| 84 | 118 | 162 | 190 | 280 | 279 | 307 | 307 | 360 |
| 85 | 128 | 162 | 238 | 257 | 270 | 295 | 377 | 342 |
| 86 | 112 | 171 | 259 | 268 | 279 | 364 | 352 | 342 |
| 87 | 107 | 189 | 244 | 278 | 288 | 325 | 323 | 387 |
| 88 | 115 | 198 | 256 | 274 | 279 | 277 | 307 | 378 |
| 89 | 113 | 189 | 268 | 272 | 315 | 364 | 386 | 378 |
| 90 | 118 | 216 | 244 | 316 | 360 | 298 | 361 | 360 |
| 91 | 146 | 171 | 247 | 311 | 342 | 322 | 359 | 360 |
| 92 | 139 | 171 | 277 | 286 | 360 | 310 | 361 | 414 |
| 93 | 125 | 198 | 289 | 296 | 306 | 361 | 350 | 351 |
| 94 | 151 | 198 | 265 | 319 | 333 | 376 | 415 | 405 |
| 95 | 140 | 180 | 259 | 317 | 324 | 364 | 359 | 396 |
| 96 | 127 | 198 | 253 | 325 | 342 | 370 | 379 | 360 |
| 97 | 137 | 216 | 256 | 293 | 288 | 376 | 404 | 459 |
| 98 | 112 | 225 | 241 | 268 | 360 | 355 | 379 | 387 |
| 99 | 107 | 207 | 262 | 269 | 342 | 370 | 368 | 414 |
| 100 | 115 | 153 | 256 | 283 | 342 | 367 | 424 | 468 |
以下にポイントごとに求めた各桁の数の総和を$10^6$以下の範囲で示します。
| $n$ | $2^n$ | $3^n$ | $4^n$ | $5^n$ | $6^n$ | $7^n$ | $8^n$ | $9^n$ |
|---|---|---|---|---|---|---|---|---|
| $1$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| $10$ | 7 | 27 | 31 | 40 | 36 | 43 | 37 | 45 |
| $10^2$ | 115 | 153 | 256 | 283 | 342 | 367 | 424 | 468 |
| $10^3$ | 1366 | 2142 | 2704 | 3172 | 3519 | 3598 | 3871 | 4338 |
| $10^4$ | 13561 | 21663 | 26995 | 31117 | 34866 | 38095 | 41194 | 42426 |
| $10^5$ | 135178 | 214074 | 270913 | 313339 | 348813 | 379429 | 407728 | 428994 |
| $10^6$ | 1351546 | 2146509 | 2708644 | 3145729 | 3500280 | 3804451 | 4059064 | 4296447 |
