問題#B006 ★★☆☆
整数 $a$、$b$ について $a^2+b^2$ が$7$の倍数であるならば、$a$、$b$ はいずれも$7$の倍数であることを示せ。
《ポイント》
#B005で扱った平方剰余の出番です。$7$を法として考えます。
《解答例》
$m$を整数とすると、すべての整数は$7m$、$7m \pm 1$、$7m \pm 2$、$7m \pm 3$のいずれかの形で表される。
$7m$と表されるとき、$(7m)^2=49m^2$であり、$7$で割った余りは$0$である。
$7m \pm 1$と表されるとき、$(7m \pm 1)^2=49m^2 \pm 14m +1$であり、$7$で割った余りは$1$である。
$7m \pm 2$と表されるとき、$(7m \pm 2)^2=49m^2 \pm 28m+4$であり、$7$で割った余りは$4$である。
$7m \pm 3$と表されるとき、$(7m \pm 3)^2=49m^2 \pm 42m+9$であり、$7$で割った余りは$2$である。
よって平方数を$7$で割った余りは$0$、$1$、$2$、$4$に限られる。
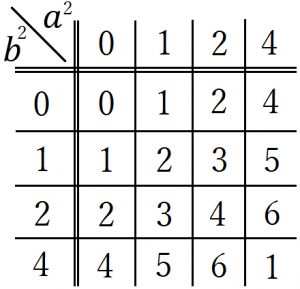
以上の結果より、$a^2+b^2$を$7$で割った余りは以下の表のようになる。
表より、$a、b$のいずれか一方でも$7$の倍数でないとき $a^2+b^2$ を$7$で割った余りは$0$になりえない。 故に $a^2+b^2$ が$7$の倍数であるならば、$a$、$b$ はいずれも$7$の倍数であることが示された。
□
《コメント》
平方剰余に頼る以外に上手い解答は書けなさそうですが、平方剰余の力はまだまだこんなものではありません・・・(笑)。