その他の問題
【ベータ関数に関する問題】
横浜市立大学(2015年/理系第1問)
【完全数に関する問題】
東京大学オープン模試(2018年第1回/理系第5問(河合塾))
正の整数 $N$ に対し、$N$ の正の約数($1$ と $N$ も含む)の総和を $S(N)$ で表す。例えば$$S(6)=1+2+3+6=12$$である。$N$ が正の整数 $n$ と $2<p<q$ をみたす素数 $p$、$q$ を用いて$$N=2^n pq$$と表されるとき、以下の問に答えよ。
(1)$\dfrac{S(N)}{N}<4$ が成り立つことを示せ。
(2)$S(N)=2N$ となるような $n$、$p$、$q$ は存在しないことを示せ。
(3)$S(N)=kN$(kは正の整数)となるような $k$ と $N$ の組をすべて求めよ。
【相反方程式に関する問題】
札幌農学校予科(1905年/(土木/林学)第4問)
$6x^4+5x^3−38x^2+5x+6=0$ を解け。
九州歯科大学(2013年/第3問)
奈良県立医科大学(2017年/推薦第3問)
横浜市立大(2018年/理系大問Ⅱ)
大阪大学(2018年/前期理系第2問)
【レイリーの定理に関する問題】
慶應義塾大学(1992年/(理工)第5問)
京都府立大学(2016年/理系第1問)
九州大学オープン模試(2017年/理系第4問(河合塾))
(著作権の関係で全文の掲載は控えさせて頂きます)
【コーシー・シュワルツの不等式に関する問題】
奈良県立医科大学(2014年/後期第2問)
信州大学(2015年/理系第4問) ※確率分野からの出題
【放物線 $\sqrt{x}+\sqrt{y}=1$ に関する問題】
神戸大学(1969年/理系第7問)
千葉大学(1988年/前期理系第5問)
東北大学(1990年/前期共通第1問)
工学院大学(1995年/前期第?問)
琉球大学(2008年/前期理系第2問)
【カージオイド(心臓形)に関する問題】
お茶の水女子大学(1992年/(物理)前期第5問)
お茶の水女子大学(1996年/(数)前期第7問/(物理)前期第5問)
【アステロイド(星芒形)に関する問題】
九州大学(1990年/後期(工)第4問)
お茶の水女子大学(1999年/(数)前期第7問)
【等角螺旋に関する問題】
神戸大学(2000年/後期理系第4問)
【シグモイド関数に関する問題】
金沢大学(2004年/前期理系第4問)
山梨大学(2015年/前期理系(生命環境/工)第1問(3))
関数 $f(x)=\dfrac{1}{1+e^{-x}}$ の増減、グラフの凹凸、変曲点を調べて、そのグラフをかけ。
横浜市立大学(2017年/前期理系第1問(3))
関数$f(x)$を$$y=\dfrac{1}{1+e^{-x}}$$とする。このとき、導関数$f^{\prime}(x)$の最大値を求めよ。
山梨大学(2017年/前期理系(生命環境/工)第4問)
秋田大学(2021年/前期大問(5))
関数 $f(x)=\dfrac{1}{1+e^{x}}$ について、次の問いに答えなさい。
(ⅰ)$x$が実数全体を動くとき、$f(x)$のとりうる値の範囲を求めなさい。
(ⅱ)定積分 $\displaystyle \int_{0}^{1} f(x) \, d x$ を求めなさい。
(ⅲ)$a$を実数とする。点$(a,f(a))$における曲線 $y=f(x)$ の接線を$\ell$とし、$\ell$と直線 $y=2$ との交点を$\mathrm{P}$、と直線 $y=-1$ との交点を$\mathrm{Q}$とする。このとき、線分$\mathrm{PQ}$の長さが最小となる$a$の値を求めなさい。
【曲率・曲率半径に関する問題】
横浜国立大学(1987年/前期(工)第5問)
室蘭工業大学(1989年/第4問)
曲線 $y=\cos \pi x$ 上に定点$\mathrm{A}(0,1)$と動点$\mathrm{P}(x,y)$(ただし、$0<|x|<1$)をとる。この2点を通り$y$軸上に中心をもつ円を$C$とする。点$\mathrm{P}$を点$\mathrm{A}$に限りなく近づけると、円$C$の半径はどんな値に近づくか。
防衛医科大学(1995年/第4問)
埼玉大学(2008年/(理(数学))第4問) ※$y=\log x$ に関する問題
【正多面体に関する問題】
名古屋市立大学(1969年/第1問小問(1))
辺の長さが$a$の正八面体(合同な$8$つの正$3$角形で囲まれている立体)について、次の問いに答えよ。
(a)相対する頂点の間の距離を求めよ。
(b)相対する平行な面の間の距離を求めよ。
名古屋市立大学(1975年/第1問小問(1))
(1)1辺の長さが1の立方体がある。この立方体の$8$つのかどから合同な正三角錐を切り捨て、立方体のもとの面が正多角形になるようにする。このようにして得られる立体の体積を求めよ。
東京大学(1990年/理科第3問) ※正八面体
お茶の水女子大学(1991年/前期理系第3問)
半径$1$の球に内接する正四面体の$1$辺の長さを求めよ。
北海道大学(2005年/前期文系第4問/前期理系第5問)
半径$1$の球に内接する正四面体の一辺の長さを求めよ。
東京大学(2008年/理科第3問) ※正八面体
東京医科歯科大学(2010年/第2問) ※立方体と正八面体
名古屋市立大学(2012年/(医)第4問)
一辺の長さが$a$の正八面体の体積と、その正八面体に内接する球、外接する球の半径を求めよ。
奈良教育大学(2015年/(教育)第1問)
一辺の長さが$a$の正四面体$\mathrm{ABCD}$の体積を$a$で表せ。
芝浦工業大学(2016年/第3問) ※正二十面体
順天堂大学(2016年/(医)第2問) ※正二十面体
東北大学(2018年/AOⅡ期(工)第1問) ※正八面体
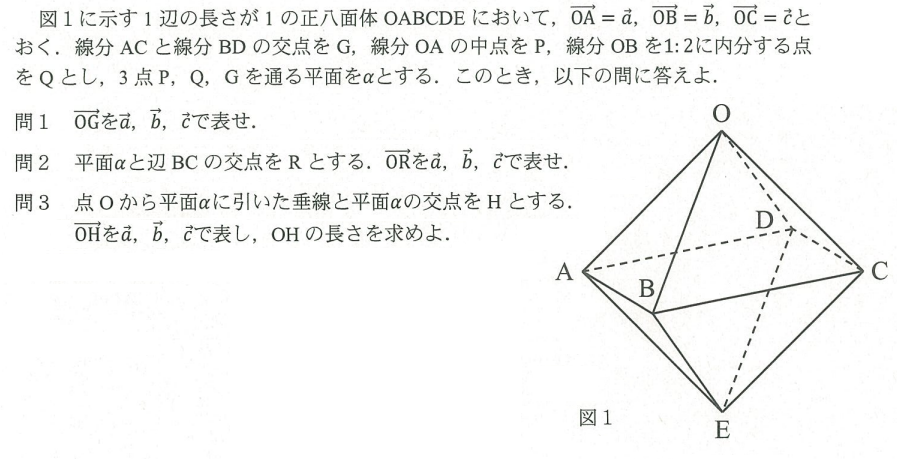
大阪大学(2018年/文系第3問/理系第4問) ※正八面体
杏林大学(2018年/(医)第2問)
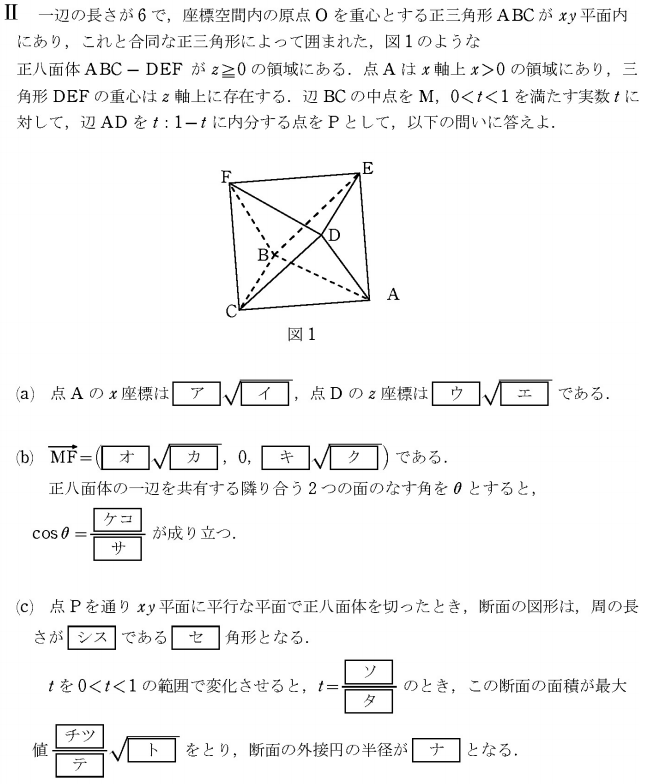
東京大学(2019年/理科第3問) ※正八面体
【空間幾何に関するその他の問題】
京都大学(1999年/後期理系第4問) ※合同四面体
$\triangle \mathrm{ABC}$は鋭角三角形とする。このとき、各面すべてが$\triangle \mathrm{ABC}$と合同な四面体が存在することを示せ。
大阪医科大学(2015年/後期第2問) ※合同四面体
四面体$\mathrm{OABC}$は、各面が互いに合同な三角形である。$\triangle \mathrm{ABC}$の辺の長さを $\mathrm{BC}=a$、$\mathrm{CA}=b$、$\mathrm{AB}=c$ として、$a$、$b$、$c$は互いに異なるとする。辺$\mathrm{OA}$、$\mathrm{OB}$、$\mathrm{OC}$の中点をそれぞれ$\mathrm{A_1}$、$\mathrm{B_1}$、$\mathrm{C_1}$、辺$\mathrm{BC}$、$\mathrm{CA}$、$\mathrm{AB}$の中点をそれぞれ$\mathrm{L}$、$\mathrm{M}$、$\mathrm{N}$とする。
(1)$\triangle \mathrm{OAB}$の2辺$\mathrm{OA}$、$\mathrm{OB}$の長さをそれぞれ$a$、$b$、$c$で表せ。
(2)3 本の直線$\mathrm{LA_1}$,$\mathrm{MB_1}$,$\mathrm{NC_1}$は一点で交わることを示せ。
(3) 3 本の直線$\mathrm{LA_1}$,$\mathrm{MB_1}$,$\mathrm{NC_1}$は互いに直交することを示せ。
京都大学(2018年/前期理系第6問/文系第4問)
四面体$\mathrm{ABCD}$は $\mathrm{AC}=\mathrm{BD}$、$\mathrm{AD}=\mathrm{BC}$ を満たすとし、辺 $\mathrm{AB}$ の中点を $\mathrm{P}$ 、辺 $\mathrm{CD}$ の中点を $\mathrm{Q}$とする。
(1)辺 $\mathrm{AB}$ と線分 $\mathrm{PQ}$ は垂直であることを示せ。
(2)線分 $\mathrm{PQ}$ を含む平面 $\alpha$ で四面体 $\mathrm{ABCD}$ を切って2つの部分に分ける。このとき、2つの部分の体積は等しいことを示せ。
京都大学(2019年/特色入試第4問) ※四面体
四面体 $\mathrm{ABCD}$ の面および内部から一直線上にない3点 $\mathrm{P、Q、R}$ を選ぶ。このとき、三角形 $\mathrm{PQR}$ の面積は四面体 $\mathrm{ABCD}$ の4つの面の面積のうち最大のものを超えないことを示せ。
茨城大学(2019年/前期(理)第1問) ※四面体

【バーゼル問題に関する問題】
京都府立医科大学(1975年/第4問)
愛知県立大学(2009年/情報科学部第4問)
以下の問いに答えよ。
(1)$0<a<b$ であるとき、$$\dfrac{b-a}{b^2}<\int_{a}^{b} \dfrac{1}{x^2}dx$$が成り立つことを示せ。
(2)$n$を$2$以上の自然数としたとき、$$\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+\cdots+\dfrac{1}{n^2}<1-\dfrac{1}{n}$$が成り立つことを示せ。
慶応義塾大学(2020年/医学部第3問)
【不等式$(a+b)^n \leqq 2^{n-1}(a^n+b^n)$に関する問題】
東京都立大学(1997年/(人文/経済)前期第1問)
$a$、$b$は正の実数とする。
(1)不等式$$(a+b)^2 \leqq 2(a^2+b^2)$$を証明せよ。
(2)$2$以上のすべての自然数$n$に対して、不等式$$(a+b)^n \leqq 2^{n-1}(a^n+b^n)$$を数学的帰納法を使って証明せよ。
お茶の水女子大学(1997年/(数)前期第6問)
どんな正の数$x$、$y$に対しても不等式$$(x+y)^4 \leqq c^3(a^4+b^4)$$が成り立つような$c$の範囲を求めよ。
東京工業大学(1999年/前期第1問)
正の実数$a$、$b$、$p$に対して、
$A=(x+y)^p$ と $B=2^{n-1}(a^n+b^n)$
の大小関係を調べよ。
埼玉大学(2004年/(工)前期第3問)
任意の正数$x$に対して次の不等式が成り立つような正の定数$a$の範囲を求めよ。$$2^{a-1}(x^a+2^a) \geqq (x+2)^a$$
関西大学(2020年/(総合情報)後期第2問)
次の問いに答えよ.
(1)$t \geqq 1$ のとき,任意の自然数$n$に対して$$t^{n+1}+1-t^{n}-t \geqq 0$$が成り立つことを示せ.
(2)を正の数とする.自然数$n$に対して$$(a+b)^n \leqq 2^{n-1}(a^n+b^n)$$が成り立つことを帰納法を用いて示せ.
【直線 $x=y$ に関して対称な放物線の問題】
三重大学(1995年/前期理系(生物資源)第3問)
実数 $a \geqq 0$ に対して、関数 $y=x^{2}+a$ のグラフと関数 $x=y^{2}+a$ のグラフを考える.
(1) 2つの曲線が接するときの$a$の値を求めよ.
(2) 2つの曲線の距離を表す関数$d(a)$を求めよ.
東京大学(2017年/理科第5問)
$k$を実数とし、座標平面上で次の$2$つの放物線$C$、$D$の共通接線について考える。$$C:y=x^2+k$$ $$D:x=y^2+k$$
(1)直線 $y=ax+b$ が共通接線であるとき、$a$を用いて$k$と$b$を表せ。ただし $a \ne -1$ とする。
(2)傾きが$2$の共通接線が存在するように$k$の値を定める。このとき、共通接線が$3$本存在することを示し、それらの傾きと$y$切片を求めよ。
【$\log x$に接する曲線の問題】
東京大学(2015年/理科第3問)
明治大学(2019年/(理工)第3問)
以下の問に答えよ。解答は最終結果だけでなく、途中経過も記述せよ。
$n$を自然数、$a$を正の実数とする。座標平面上の曲線 $y=ax^n$ と曲線 $y=\log x$ は点$\mathrm{P}$で接しているとする。すなわち、これらの曲線は点$\mathrm{P}$を共有し、点$\mathrm{P}$で共通の接線をもつ。点$\mathrm{P}$の$x$座標を $p$ とおく。ただし、$\log x$ はどの自然対数である。また、自然対数の底を $e$ で表す。
(1)$a$と$p$をそれぞれ$n$の式で表せ。
(2)曲線 $y = ax^n$ と直線 $y=p$ および$x$軸で囲まれる部分の面積 $S_n$を($a$と$p$を含まない)$n$の式で表せ。
(3)曲線 $y = \log x$ と直線 $y=p$ および$x$軸で囲まれる部分の面積を($a$と$p$を含まない)$n$の式で表せ。
(4)極限値 $\displaystyle \lim_{n \to \infty} \dfrac{T_n}{S_n}$ を求めよ。必要なら、$t>0$ に対して$$1-t+\frac{t^{2}}{2}-\frac{t^{3}}{6}<e^{-t}<1-t+\frac{t^{2}}{2}$$が成立することを証明せずに用いてよい。
※2015年東大理科の類題
奈良県立医科大学(2017年/推薦第3問)
横浜市立大(2018年/理系大問Ⅱ)
大阪大学(2018年/前期理系第2問)
【定数の評価に関する問題】
お茶の水女子大学(1995年/(数)前期第7問)
$\dfrac{100}{120}< \sin 1 <\dfrac{101}{120}$ を示せ。ただし、$\sin 1$ の $1$ はラジアンの意味である。
山梨大学(1999年/(工)前期第1問)
$f(x)=\log(1+x)-(x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\dfrac{x^4}{4})$
$g(x)=\log(1+x)-(x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\dfrac{x^4}{4}+\dfrac{x^5}{5})$
について次の問に答えよ。
(1)導関数$f'(x)$、$g'(x)$を各々求め、簡単な式で表せ。
(2)$x>-1$ で $\log(1+x) \leqq x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\dfrac{x^4}{4}+\dfrac{x^5}{5}$ となることを示せ。
(3)$\dfrac{1}{2}<\log 2<\dfrac{4}{5}$ であることを示せ。
三重大学(2001年/(教育)前期第1問)
(1)$2^{10}=1024>1000$ を利用して $\log_{10}2 >0.3$ を示せ。
(2)$M、N$を正の実数とするとき、不等式$$\log_{10}(M+N) \geqq \dfrac{1}{2}(\log_{10}M+\log_{10}N)+\log_{10}2$$が成り立つことを示せ。
(3)(1)、(2)を利用して $\log_{10}13>1.1$ を示せ。
東京大学(2003年/前期理系第6問)
円周率が$3.05$より大きいことを証明せよ。
大阪医科大学(2009年/前期第3問)
(1)$0 \leqq x \leqq \dfrac{1}{3}$ のとき、つぎの不等式が成り立つことを示せ。$$2(1+x^2) \leqq \dfrac{1}{1+x}+\dfrac{1}{1-x}= \dfrac{2}{1-x^2} \leqq 2(1+x^2)+\dfrac{x^2}{4}$$
(2)不等式 $\dfrac{56}{81} \leqq \log 2 \leqq \dfrac{56}{81}+\dfrac{1}{324}$ を示せ。
横浜市立大学(2010年/前期(医)第4問)
$a>0$ とする。以下の問いに答えよ。
(1)$0 \leqq x \leqq a$ をみたす $x$ に対して$$1+x \leqq e^{x} \leqq 1+\dfrac{e^{a}-1}{a} x$$を示せ。
(2)(1)を用いて$$1+a+\dfrac{a^{2}}{2}<e^{a}<1+\dfrac{a}{2}\left(e^{a}+1\right)$$を示せ。
(3)(2)を用いて$$2.64<e<2.78$$を示せ。
大阪医科大学(2010年/前期第2問)
自然数$n$に対して次のようにおく。$$a_n=1+\dfrac{1}{2}+\cdots+\dfrac{1}{n}-\log n 、$$ $$b_n=1+\dfrac{1}{2}+\cdots+\dfrac{1}{n}-\log (n+1)$$
(1)$n \geqq 2$ のとき、$a_n<a_{n-1}$、$b_n>b_{n-1}$ を示せ。
不等式 $1.09<\log 3 <1.1$ を用いて、(2)、(3)に答えよ。
(2)$n \geqq 2$ のとき、$b_n>0.4$ を示せ。
(3)$n \geqq 3$ のとき、$0.4<a_n<0.75$ を示せ。
(※管理人注:$\displaystyle \lim_{n \to \infty} a_n$ は「オイラー定数」$\gamma = 0.5772156…$ に収束する)
新潟大学(2012年/理系前期第2問)
信州大学(2014年/後期(医)第5問/(理)第2問)
$e$を自然対数の底とする。このとき、以下の問いに答えよ。
(1)自然数$n$に対し、$$0 \leqq \displaystyle \int^{1}_{0} t^{n}e^{1-t}dt<e-1$$を示せ。
(2)正の数$a$と自然数$n$に対し、$$e^a=1+ \displaystyle \sum^{n}_{k=1} \dfrac{a^k}{k!} + \dfrac{1}{n!} \displaystyle \int^{a}_{0} t^{n}e^{a-t}dt$$が成り立つことを示せ。
(3)(1)と(2)を用いて $2.4<e<3$ を証明せよ。
【その他の諸定理・公式に関する問題】
名古屋市立大学(1967年/前期第1問(1))
正弦定理を述べて、これを証明せよ。
名古屋市立大学(1968年/(医/薬)第1問)
等式 $\displaystyle \lim_{x \to 0} \dfrac{\sin x}{x}=1$ を証明せよ。
東京大学(1999年/前期共通第1問)
※三角比の定義・加法定理の証明
三重大学(2003年/(教育)前期第3問)
絶対値が$1$で偏角が$\theta$の複素数を$z$とし、$n$を正の整数とする。
(1)$z^n$を$\theta$で表す式を、三角関数の加法定理を用いて、帰納法で証明せよ。
(2)$|1-z^2|$を$\theta$の関数で表せ。
(3)$\displaystyle \sum_{k=1}^n \sin 2k \theta$ を計算せよ。
順天堂大学(2007年/(医)第3問)
次の問に答えよ。答えだけではなく式・説明など解答の途中の経過を示すこと。
(1)関数$f(x)$が $x = a$ で微分可能とはどういうことか、説明せよ。
(2)「関数 $y = f(x)$ が $x = a$ で微分可能である」と「関数 $y = f(x)$ が $x = a$ で連続である」とはどのような関係にあるか述べよ。またそれを証明せよ。
(3)ある区間 $a<x<b$ で微分可能な関数$f(x)$、$g(x)$について導関数の定義から関数の積$f(x)g(x)$の導関数を求めよ。
佐賀大学(2008年/前期文系第1問(1))
※正弦定理の証明
順天堂大学(2008年/(医)第3問)
次の問に答えよ。答えだけではなく式・説明など解答の途中の経過を示すこと。
(1)円周角と中心角の定義を書き、その関係を述べよ。
(2)円周角が直角である場合、上の関係を図を用いて説明せよ。
(3)正弦定理を述べ、それを証明せよ。
順天堂大学(2009年/(医)第3問)
次の問に答えよ。答えだけではなく式・説明など解答の途中の経過を示すこと。
(1)関数 $y = f(x)$ の値域の定義を述べよ。
(2)関数 $y = f(x)$ があるとき、逆関数が存在する条件と逆関数の定義を述べよ。
(3)対数関数を指数関数により定義せよ。
(4)対数関数の底の変換公式を書きなさい。さらに、指数法則より底の変換公式を示しなさい。
三重大学(2009年/理系前期第2問)
工学部(1)$0$以上の2数$\alpha$、$\beta$について、相加平均$\dfrac{\alpha+\beta}{2}$が相乗平均$\sqrt{\alpha \beta}$以上であることを証明せよ。
医学部(2)$0$以上の数$\alpha$、$\beta$、$\gamma$について、相加平均$\dfrac{\alpha+\beta+\gamma}{3}$が相乗平均$\sqrt[3]{\alpha \beta \gamma}$以上になることを示せ。
順天堂大学(2010年/(医)第3問)
※有理数・無理数に関する問題
順天堂大学(2011年/(医)第3問)
※剰余の定理に関する問題
順天堂大学(2012年/(医)第3問)
※共役複素数と多項式の解に関する問題
大阪大学(2013年/文系前期第1問)
$xy$平面において、点$(x_0,y_0)$と直線 $ax+by+c=0$ の距離は$$\dfrac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$$である。これを証明せよ。
大阪大学(2013年/理系前期第1問)
※$\sin x$ の導関数を定義から導出させる問題
奈良教育大学(2013年/(教育)第5問)
三角形の$3$辺の垂直二等分線は$1$点で交わることを証明せよ 。
順天堂大学(2014年/(医)第3問)
※三角形の内心に関する問題(ベクトル)
上智大学(2015年/(理工/経済)第1問)
※対数の定義に関する問題
高知大学(2016年/AO(医)総合問題Ⅰ/大問Ⅱ)
※ヘロンの公式に関する問題
順天堂大学(2016年/(医)第3問)
※三角不等式に関する問題
順天堂大学(2017年/(医)第3問)
※イェンゼンの不等式に関する問題(凸関数)
奈良教育大学(2018年/(教育)第4問)
底面の半径が$r$、高さが$h$である円錐の体積$V$は$\dfrac{1}{3}\pi r^2 h$となることを、積分を用いて証明せよ。
順天堂大学(2018年/(医)第3問)
※三角形の重心と外心が一致するための必要十分条件
藤田医科大学(2018年/(医)第2問)
$x=\cos \dfrac{\pi}{180}$ とおく。次の問いに答えよ。
(1)$\cos \dfrac{\pi}{60}$ を $x$ の3次式で表せ。
(2)任意の正の整数 $n$ に対し、$\cos \dfrac{n\pi}{180}$ は $x$ の $n$ 次式で表されることを証明せよ。
(3)$x$ は無理数であることを証明せよ。ただし、素数の平方根が無理数となることを証明なしに用いてもよい。
藤田医科大学(2019年AO入試/(医)問題2)
すべての実数$x$に対して関数$f(x)$と$g(x)$が微分可能であるとき、次の問いに答えよ。
(1)$f(x)$の導関数$f^{\prime}(x)$の定義を書け。
(2)(1)の導関数の定義に基づき$$\{f(x) g(x)\}^{\prime}=f^{\prime}(x) g(x)+f(x) g^{\prime}(x)$$を証明せよ。
(3)$\dfrac{1}{f(x)}$ が微分可能であるとき、(1)の導関数の定義に基づき$$\left\{\dfrac{1}{f(x)}\right\}^{\prime}=-\dfrac{f^{\prime}(x)}{\{f(x)\}^{2}}$$を証明せよ。ただし、$f(x) \ne 0$ とする。
