4次関数(複接線)の問題
東北大学(1959年/数学Ⅰ(代数)第1問)
(1)四次式$$f(x)=4x^4+ax^3-11x^2-30x+25$$が二次式の平方になるように$a$の値を定めよ。
(2)この$a$の値に対する$\sqrt{f(x)}$の $-3 \leqq x \leqq 0$ における最大値を求めて理由を付記せよ。
※実質的に2次関数の問題。
京都大学(1959年/数学Ⅱ第1問抜粋)
四次方程式 $x^4+px^3+8x^2+px+1=0$ が4つの実根をもつようにするために、係数$p$に与えるべき実数値の範囲を求めよ。
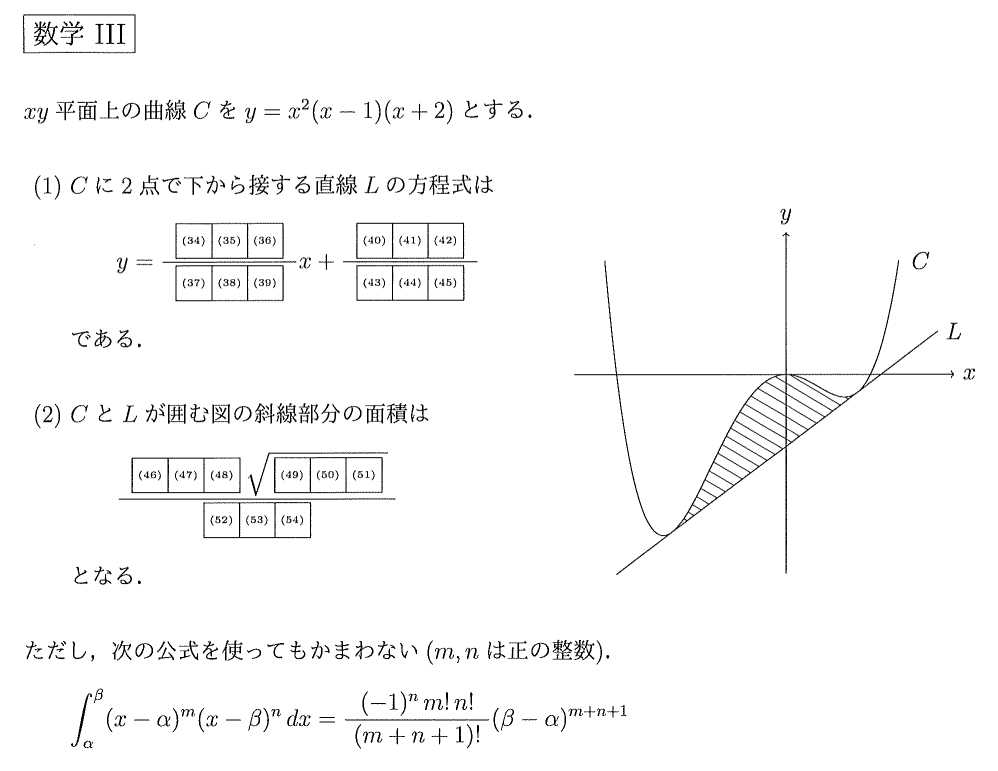
大阪大学(1959年/数学Ⅲ第2問)
北海道大学(1961年/文系(数学Ⅲ)第2問)
$f(x)=x^4-4x^3+2ax^2$ について、次の問いに答えよ。
(1)$f(x)$が極大値をもたないのは$a$の値がどんな範囲のときか。
(2)$f(x)$が極大値をとるとき、極大値を与える$x$の値を求めよ。
九州大学(1961年/文系(数学Ⅱ)第1問)
北海道大学(1963年/文系(数学Ⅲ)第3問)
大阪大学(1963年/前期文理共通第2問)
横浜国立大学(1964年/前期理系(工)第4問)
横浜国立大学(1966年/前期文系(経済)第5問)
京都大学(1967年/前期理系第4問/前期文系第3問)
九州大学(1970年/理系第3問)
早稲田大学(1970年/理工第4問)
※4次関数の因数分解に関する問題。(領域図示)
京都大学(1974年/前期理系第3問)
横浜国立大学(1978年/前期理系(工)第3問)
東北大学(1979年/前期(教育)第3問)
$f(x)=x^4-x^3+x^2-x$ とする。
(1)曲線 $y=f(x)$ が$x$軸と交わる点の座標を求めよ。
(2)これらの点におけるこの曲線の接線の方程式を求めよ。
(3)これらの接線とこの曲線で囲まれた部分の面積を求めよ。
横浜国立大学(1981年/前期文系(経済)第4問)
東京工業大学(1982年/第3問)
曲線 $y=x^4-6x^2$ を$C$とし、不等式 $y>x^4-6x^2$ で定まる領域内の点$P(\alpha,\beta)$から異なる4本の接線が$C$に引けるとする。このとき点$P$の動きうる領域$D$を求め図示せよ。
横浜国立大学(1982年/前期文系(経済)第4問)
横浜国立大学(1985年/前期文系(経済)第4問)
筑波大学(1987年/文理共通第2問)
曲線 $y=x^4-x^3$ 上の1点$A=(\alpha,{\alpha}^4-{\alpha}^3)$における接線を$l$とする。
(1)$l$の方程式を求めよ。
(2)$l$が上の曲線と$A$以外の点で再び接するように$\alpha$の値を定めよ。
京都大学(1988年/文科A第1問)
九州大学(1989年/文系第3問)
※複接線の問題。
東京大学(1990年/前期文系第2問)
京都大学(1990年/後期理系(工/農/薬/医)第4問)
大阪大学(1990年/前期理系第3問)
点$(a,0)$を通り、曲線 $y=x^4-2x^2+1$ に接する直線が$x$軸以外にただ1本存在するような$a$の値をすべて求めよ。
大阪大学(1990年/前期文系第3問)
点$(1,0)$を通り、曲線 $y=x^4-2x^2+1$ に接する直線の方程式をすべて求めよ。
早稲田大学(1991年/政経第1問抜粋)
※複接線の問題。(面積計算)
名古屋大学(1991年/前期共通第1問)
4次関数のグラフが、$y$軸に平行なある直線に関して対称になるための係数$a,\,b,\,c,\,d$の間の関係式を求めよ。
東京工業大学(1993年/第3問)
筑波大学(1993年/文理共通第3問)
曲線 $y=x^4-2x^2$ の接線が、この曲線と接点以外に異なる2点で交わる条件を求めよ。また、このとき、接線から接点と2つの交点で切り取られる2つの線分の長さが等しくなるときの接点の座標を求めよ。
早稲田大学(1993年/政経第1問)
※面積の計算問題。
東北大学(1993年/後期理系第3問)
※単接線と4次関数で囲まれる部分の面積の計算問題。
東北大学(1995年/前期文系第2問)
関数 $-x^4+x^3+x^2-x-|x^4+x^3-x^2-x|$ の増減を調べ、そのグラフを描け。
大阪市立大学(1995年/前期理系第1問)
大阪大学(1995年/後期理系第1問)
大阪大学(1996年/前期文系第3問)
京都大学(2001年/文系第1問)
※理系第2問の類題。理系の問題は5次式バージョン。
大阪大学(2001年/前期理系第2問)
$f(x)=x^4+x^3-3x^2$ とおく。曲線 $y=f(x)$ に点$(0,a)$から接線がただひとつ引けるとししかもその接線はただ1点でこの曲線に接するとする。このときの$a$の値を求めよ。
※1990年の類題。1990年の問題は「すべて求めよ。」となっており、実際に答えは複数存在します。2001年の問題では単に「求めよ。」となっており、実際に答えとなる$a$の値は一つしか存在しません。阪大は受験生に優しいですね。
徳島大学(2001年/(薬/歯/医)第4問)
東北大学(2002年/文理共通第1問)
※4次方程式の問題。(虚数解含む)
京都大学(2002年/理系第3問/文系第1問)
九州大学(2003年/後期理系(工)第2問抜粋)
早稲田大学(2003年/理工第1問)
※複素平面と絡んだ4次方程式の問題。
東北大学(2005年/後期理系第2問)
※4次方程式の問題。(虚数解含む)
弘前大学(2007年/前期理系(理工/医)第3問)
$f(x)=x^4+2x^3-3x^2+x+1$ とする。
(1)4次式 $f(x)-mx-n$ が$2$次式の$2$乗となるような定数$m、n$の値を求めよ。
(2)$m、n$が(1)で求めた値のとき、直線 $y=mx+n$ と曲線 $y=f(x)$ によって囲まれた部分の面積を求めよ。
大阪市立大学(2007年/前期理系第2問)
津田塾大学(2009年/学芸(数学科)第2問)
次数が $n$ の多項式$$f(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$$が $f(x) = (x – \alpha)^n$ という形に因数分解できるとき、$\alpha$ を方程式 $f(x) = 0$ の $n$ 重解ということにする。
(1)方程式 $x^2 + ax + b = 0$ が2重解 $\alpha$ を持つとする。$a$、$b$ が整数のとき、$\alpha$ は整数であることを示せ。
(2)方程式 $x^4 + px^3 + qx^2 + rx + s=0$ が4重解 $\beta$ を持つとする。$p$、$q$ が整数のとき、$\beta$ は整数であり、$r$、$s$ も整数であることを示せ。
横浜市立大学(2010年/医(医)第1問(1))
4次方程式$$a x^{4}+b x^{3}+c x^{2}+d x+e=0$$を考える。ただし, $a,b,c,d,e$ は定数で, $a \ne 0$ とする。$x=t+\alpha$ ($\alpha$は定数)とおいて, $t$に関する4次方程式$$t^{4}+C t^{2}+D t+E=0$$の形にする。このとき $D=0$ となる条件式を $a,b,c,d$ を用いて表せ。
愛知県立大学(2010年/情報科第2問)
東大プレ(2014年/第2回理系(代ゼミ))
※4次関数が複接線を持つ条件に関する問題。(著作権の関係で問題文の掲載を控えさせて頂きます)
大阪大学(2018年/前期理系第2問)
慶應義塾大学(2022年/環境情報第3問)