大学の有機化学:立体化学を知る(混成軌道編)
$\require{mhchem}$
✎すべての分子は立体的
普段、皆さんは化合物の構造を描く際に、どれだけ立体的なイメージを持っているでしょうか?
皆さんが分子の構造式を書くときは紙に書くと思いますが、紙というのは平面です。しかし実際の分子は三次元的な立体構造を有しており、原子も実際には点ではなく実体を持った粒状の立体物です。
また原子間の結合様式によって結合の角度や二面角も変わってきます。例えば以下の構造式で表される分子はアダマンタン(adamantane)と呼ばれる有機化合物ですが、どんな立体構造をしているか分かりますか?
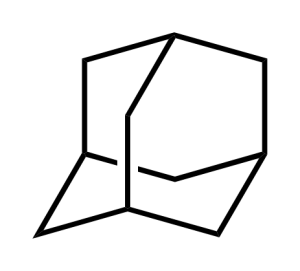
3次元的に表現すると以下のような構造となります。(マウス(スマートフォンならスワイプ)で動かせます)
有機化学を学んでいく中で、この例のように立体構造を捉えにくい分子や、立体配置を間違えやすい分子が沢山登場します。そして何と言っても化合物を立体的に把握する能力は化合物を命名する際に必要不可欠です。また、意地悪な演習問題ではわざと立体構造の複雑な分子を用意して受験者を引っ掛けるものもあります。こうした引っ掛けに惑わされないためにも、分子の立体構造を正確に把握できる能力を身に付けておくことは有機化学を学ぶ上で非常に重要です。
✎三次元構造を決める要素:電子軌道
分子の三次元構造を理解するために避けて通れないのが「混成軌道」の概念です。原子軌道(atomic orbital:AO)や分子軌道(molecular orbital:MO)は化学結合論の知識ですが、有機化学を理論的に学ぶためにとても有用です。最初は煩わしいと思うかもしれませんが、ゆっくり理解していきましょう。
● ● ●
化合物は原子の集合体であり、互いの価電子を共有する共有結合によって分子を形作っているのですが、実際に電子そのものをやりとりするというよりは互いの原子軌道が相互作用して分子軌道を形成していると考えた方が良いかもしれません。
ここで、軌道というのは簡単に言えば「電子の収まっている領域」を指しています。原子や分子の電子状態(電子配置がどのようになっているか)はシュレディンガー方程式を解くことで求められます。その際に波動関数という複素関数を利用するのですが、波動関数は各電子につき1つずつ割り当てられており、これは空間的に電子が占める領域の数学的な表現だと解釈できます(参考:コペンハーゲン解釈)。
波動関数の絶対値の二乗が電子の存在確率に相当する・・・など、小難しい話もありますが、ここではひとまず脇に置き、各原子には「軌道」という名前の電子の(空間的な)入れ物がある、ということをしっかり理解しておいて下さい。
有機化学の分野で主に登場するのはs軌道とp軌道で、一般に次のような形状をしていると説明されます。
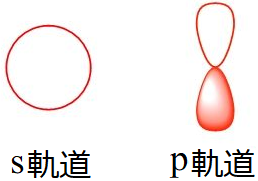
s軌道は球状で、p軌道は2個のドロップを繋げたような形状をしています。s軌道以外の電子軌道はいずれも葉(lobe)のような形をしていることから「ローブ」と呼ばれることがあります。
有機化学で主要な第2周期元素($\ce{C}、\ce{N}、\ce{O}、\ce{F}$など)の原子は1個のs軌道と3個のp軌道をもっており、これらが組み合わさって(混成して)分子軌道を形成します。
例えば1つの$\ce{s}$軌道と3つの$\ce{p}$軌道が混成して4つの混成軌道を形成する場合、以下の図のように4つの等価な「$\ce{sp^3}$混成軌道」が形成されます。軌道が混成する理由については量子化学の範囲で説明されますので、ここでは割愛します。今のところは、軌道のエネルギー準位が下がってエネルギー的に有利になるから、という風にザックリ捉えておいて下さい(このようにエネルギー準位の異なる軌道が集まって新たにエネルギー準位の等しい複数の軌道を生じることを縮退と言います)。
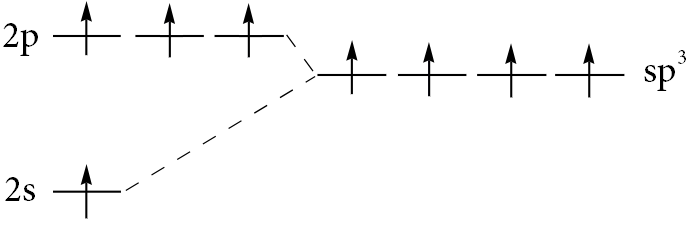 図.$\ce{sp^3}$混成軌道のエネルギー準位の概念図
図.$\ce{sp^3}$混成軌道のエネルギー準位の概念図
こうして形成された4つの$\ce{sp^3}$混成軌道はそれぞれ中心元素から電子軌道を3次元的に拡げます。このときの軌道の広がり方が分子の立体構造に大きく影響します。4つの$\ce{sp^3}$混成軌道は他の原子軌道と共有結合して電子を受け取り、1組の電子対を形成しますが、このとき各軌道は互いの電子対と電気的に反発し、できるだけ他の軌道と距離を取ろうとします。これは原子価殻電子対反発則(valence shell electron pair repulsion rule:VSEPRモデル)によって説明できますが、わざわざ小難しい話を用意する必要はありません。とにかく、電子たちにとっては次のことが重要なのです。
「電子は広いところが好き」
何をアホなことを言っているんだという方も居るかもしれませんが、これはあながち間違いではありません。量子化学などを履修した方であれば、講義の中で「箱型ポテンシャル」もしくは「井戸型ポテンシャル」というものを学んだかと思います。これによれば、電子のエネルギーは空間の次元に反比例するという結果を得ることができ、ポテンシャル空間を拡げれば拡げるほど電子の運動エネルギーは低下します。井戸型ポテンシャルのような簡単なモデルであっても電子の性質をちゃんと説明できるんですね。
つまり、電子の気持ちを代弁するならこちらの方が良いかもしれません。
「電子は低いところが好き」
「低い」というのはもちろんエネルギー準位の話です。分子内の電子には「軌道」という名前の入れ物に入らなければならない、という制約がありますが、その制約の下、電子たちはとにかくあの手この手で安定化しようと努めています。わざわざ混成軌道を形成するというのも、電子が何とかして安定化しようと努力した結果なのです。
炭素原子は$\ce{s}$軌道に2個、3つの$\ce{p}$軌道のうち2つに1個ずつ電子を持っており、結合を作るときは$\ce{s}$軌道の電子をわざわざ$\ce{p}$軌道に持ち上げて混成軌道にするのです。これには多くのエネルギーが必要となりますが、その後にできる4つの$\ce{sp^3}$混成軌道による結合の方がエネルギーが低いため、一見すると不合理な方法でもきちんと安定化することに成功しています。
● ● ●
さて、なかなか話が脱線してしまいましたが、要するに電子対はできる限り互いに離れようとするのです。これがVSEPR則が主張していることです。上記の説明も細かいところは色々突っ込めるのですが、取り敢えずは皆さんの理解を優先して先へ進みましょう。
✎分子の形を決めよう
先程の説明の通り、電子はとにかく広がりたいと思っています。つまり3次元的に考えると、中心原子から広がる軌道は互いに最大限離れるような方向に広がるということを意味しています。
したがって4つの$\ce{sp^3}$混成軌道の場合、軌道は中心から正四面体の頂点方向に向かって広がります。
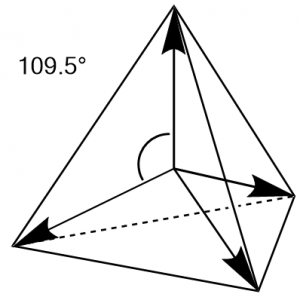
これを最もよく表しているのがメタン分子でしょう。
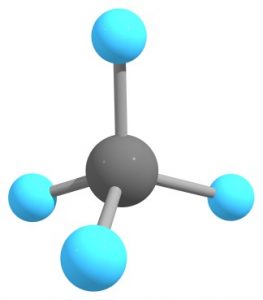
メタンの炭素原子は4つの$\ce{sp^3}$混成軌道を形成し、それぞれが正四面体の頂点方向に向かって広がっています。これに水素原子が結合してめでたくメタン分子が完成します。
3つの$\ce{sp^2}$混成軌道の場合、軌道は中心から正三角形の頂点方向に向かって広がります。
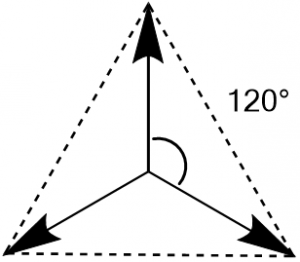
これはエチレン分子で理解することができます。
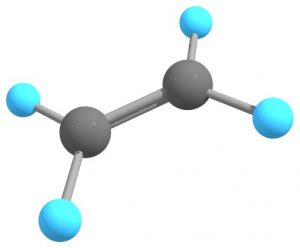
$\ce{sp^2}$混成軌道を形成する際、3つの$\ce{p}$軌道のうち2つだけが使われます。3つの混成軌道は$\sigma$結合の形成に用いられ、残りの1つは何に使われるかというと、$\pi$結合の形成に利用されます。実はこれが2重結合の由来なのです。エチレン分子の炭素間では$\sigma$結合と$\pi$結合という2本の結合が存在しており、この結合間では分子が自由に回転できません。そのため「ジアステレオマー」というキラリティが発生します。この辺の事情についてはまた後ほど詳しく見ていきます。
2つの$\ce{sp}$混成軌道の場合はお分かりだと思いますが、軌道は中心原子を挟んで反対方向、つまり一直線状に広がります。
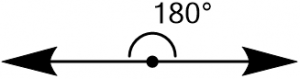
$\ce{sp}$混成軌道を有する分子の好例がアセチレンです。
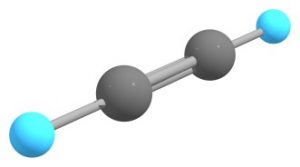
$\ce{sp}$混成軌道には$\ce{p}$軌道が1つだけしか必要ないので、他の2つの$\ce{p}$軌道はともに$\pi$結合を形成します。こうして3重結合が形成され、直線状の構造となります。二酸化炭素も同様に直線状の分子構造をとりますが、これも混成軌道の考え方によって説明することができます。
非共有電子対が何個存在するかなどを考慮して軌道の立体反発を考えると、酸素や窒素などのヘテロ原子を含んだ分子の構造がよく理解できます。軌道の概念は大学初年度の化学で学ぶと思いますが、化学を根本から理解するためには欠かせません。化学というのは電子の学問です。分子軌道をよく学べば化学反応をよく理解することができるのです。
立体化学を理解する上で重要な軌道の概念をおさらいしたところで、次節からはいよいよ大学レベルの有機化学を学んでいきます。
