量子論の夜明け(前期量子論)
✎時代背景~黒体放射の問題~
時は19世紀後半、所はヨーロッパ、とりわけドイツでは鉄鋼業が盛んであった。軍事国家として成長し続けてきたプロイセン王国では1862年、鉄血政策の名で知られるビスマルクが宰相に就任し、富国強兵策の一環としてドイツ帝国は工業化を一段と推し進めていった。
量子力学の萌芽はこの時代まで遡る。
良質の鉄を生産するには溶鉱炉の温度を正確に知る必要があった。従来は熟練の技術者の経験に基づいて溶解した鉄の発する光の色から溶鉱炉内の温度を見積もっていたが、これでは正確な温度は測定できなかった。そこで物理学者は鉄が発する光の色(正確に光の波長)で溶解した鉄の温度を測定しようと試みた。
1859年、プロイセン出身の物理学者であるキルヒホッフは、黒体輻射場のボルツマン分布は温度にのみ依存することを明らかにした。温度$T$の物体はある一定の振動数$\nu$の光を発することが知られており、キルヒホッフの理論によれば$T$と$\nu$の関数で黒体輻射場のボルツマン分布が記述できるということになる。そこで$T$と$\nu$の相関を表す関数を求めることが物理学者の主な仕事となった。プランクの輻射公式が発見されるまでに主に2つの理論式が提唱されたので、概観しておこう。ここで$U(\nu,\,T)$は単位体積あたりのエネルギー密度を表している。
・ウィーンの輻射公式(Wien’s radiation law:1896年)$$U(\nu,\,T)=\dfrac{8\pi k_B \beta}{c^3}e^{-\beta \nu /T}\nu^3$$
・レイリー・ジーンズの輻射公式(Rayleigh–Jeans radiation law:1900年~1905年)$$U(\nu,\,T)=\dfrac{8\pi k_B }{c^3}T\nu^2$$
ウィーンの輻射公式は実際に観測される黒体のスペクトルを定性的に議論することに成功してはいるものの、定量的な点で見ると誤差は大きいものだった。またはレイリー・ジーンズの輻射公式では$\nu$が赤外領域から大きくなると値が発散してしまうため、振動数が大きい領域では実験結果を説明することができない。
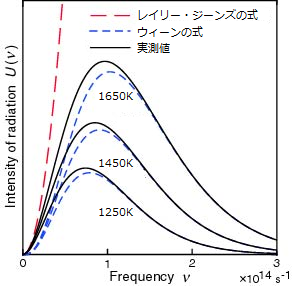 図1.黒体輻射の関数と実測値
図1.黒体輻射の関数と実測値
ドイツの物理学者マックス・プランクは、レイリー・ジーンズの式が小さい振動数の領域で実測値にフィッティングし、片やウィーンの式は振動数が大きい領域で実験結果を上手く説明できていることに着目した。これらの経験式をもとにして、実測値に高精度でフィッティングする輻射公式の理論構築が始められた。こうして1900年の10月、ベルリンで開かれた物理学協会の例会において物理学の飛躍の端緒となる画期的成果が発表されることになる。
・プランクの輻射公式(Planck’s radiation law:1900年)$$U(\nu,\,T)=\dfrac{8\pi h \nu^3}{c^3}\dfrac{1}{e^{h\nu / k_B T}-1}$$
これはプランク分布の公式とも呼ばれ、エネルギー密度の振動数に関する分布を見事に説明した。ただしこの時点では、この公式の物理的な意味や導出過程にはプランク自身も全くの理解が伴っておらず、プランクが実験データに合うように上手く設計した内挿式に過ぎなかった。この発表から2ヶ月後、プランクにより旧来の物理学の常識を打ち破る大胆な仮説が提出される。
✎エネルギーは「量子化」されている
プランクの研究成果を紹介する前に、普段我々が感じている物理の世界を振り返ってもらいたい。あるものを持ち上げるときや、道を歩くときなど、我々の運動には常にエネルギーの移動が伴う。我々はものをゆっくり、スムーズに持ち上げることができるし、自由な速さで歩くことができる。日常生活において、エネルギーは連続的に消費され、行き来するように見える。
しかしプランクが提唱した仮説ではこれが否定される。つまり、エネルギーには数えられる最小単位の量、すなわち「素量」が存在するというのである。これを「プランクの量子仮説」という。
● ● ●
《プランクの量子仮説》
振動数$\nu$をもつ電磁波のエネルギーは、エネルギー量子$h\nu$を単位として$$\varepsilon_n=nh\nu \ \ (n=0,\,1,\,2,\cdots)$$の離散値で与えられる。
● ● ●
これはエネルギーが連続的な値を取ることはできない、即ちエネルギーが量子化されているということを意味している。プランクの量子仮説は従来の物理学観、自然観からはかけ離れた考え方であったが、黒体放射の問題をうまく解決することができた。
残された問題は、有限の量のエネルギーをもつ光がどのようにして伝播するのか、という点であった。マクスウェルの電磁気学ではエネルギーの伝播速度は有限とされるため、エネルギーは連続的に移動しなければならず、エネルギーの量子化はそれまでの理論では説明がつかなかった。
✎光電効果の発見と理論の確立
ドイツの物理学者であったハインリヒ・ヘルツは1887年、電磁波が空間を伝播するというマックスウェルとファラデーの予言を立証するための実験の際に、紫外線の照射により亜鉛板が正に帯電することを見出した。これは電荷を容易に失うということを意味しており、後に弟子のレーナルトによって実験結果がまとめられ、光電効果として世に発表された。
● ● ●
《光電効果》
・光電効果はある一定以上の振動数の光を金属板に照射しなければ起こらない
・金属から放出された光電子1個あたりの運動エネルギーは照射光の強度に依存せず、照射光の振動数のみに依存する
・単位時間あたりの光電子の数は照射光の振動数に依存せず、照射光の強度のみに依存する
● ● ●
多くの物理学者が光電効果の理論的な解明に取り組んだが、これらの現象はマクスウェルの電磁気学の範疇では説明することが困難であった。そんな折、俗に奇蹟の年と呼ばれる1905年にアインシュタインが「光量子仮説」を提出する(同年にアインシュタインは後のブラウン運動に繋がる微粒子の運動の理論や特殊相対性理論に関する論文を発表しており、そのいずれもがノーベル賞級の成果であることから、1905年は奇蹟の年と呼ばれることがある)。
その概要は以下のようになる。
振動数$\nu$の光は、$h\nu$を単位とするエネルギーを有する(このような光の粒子を光子と呼ぶ)。これが金属板に照射されると金属内の電子が光のエネルギー$h\nu$を吸収する。ここで光のエネルギーを受け取った自由電子が金属の外部へと飛び出すために必要なエネルギーを仕事関数$W$と置く($W$は物質固有の値)。これより、金属から放出された後の電子の運動エネルギー$E$は$$E=h\nu-W$$で与えられる。もし$h\nu$の値が仕事関数$W$よりも小さければ $E<0$ となり電子は正の運動エネルギーをもって金属から脱出することはない。また、光子の個数が多いほど光の強度は増すため、光電子の数が照射光の強度のみに依存するという点も説明できる。
こうして光電効果はアインシュタインの光量子仮説によって説明された。$h\nu$というエネルギー素量を用いている点からも推察されるように、光量子仮説はプランクの量子仮説を基に発想されたという。
この仮説が物理学界に受け入れられるまでには少し時間を要したが、その後の様々な実験により光が量子化されていることが実証された。なお、アインシュタインはこの功績により1921年にノーベル物理学賞を受賞している。
✎原子のモデルとボーアの理論
これまで述べた通り、20世紀初頭は電子や光の物理学的な本質に迫る理論の確立が次々に行われた時代であった。このようなミクロの世界を対象とした物理学の好奇の眼は当然ながら原子の構造にも向けられていた。
当時、トムソンや長岡半太郎の原子モデルなど様々な原子の構造モデルが相次いで発表された。1911年、ラザフォードは、金箔にアルファ線を照射するという有名な実験の結果から、正電荷をもった非常に小さい原子核が原子の質量のほとんどを占めていてその周りを電子が周回している、という原子模型を提案した。これが現実に最も即しているモデルだと考えられたが、電磁気学の理論によれば、電子は円運動により電磁波を放出し、エネルギーを忽ち失って中心核へ落ち込んでいってしまう。また、電子が原子核の周囲をどのように周っているのかについても疑問の余地が残されていた。
これらの問題を解決するため、コペンハーゲン大学に私講師として勤めていたニールス・ボーアは1913年、「原子および分子の構成について」という3部にわたる論文の第1論文の中で次のような仮説を提唱した。
● ● ●
《ボーアの量子仮説》
・電子の角運動量が$\dfrac{h}{2\pi}$の自然数倍であるとき、電子は電磁波を放出せず原子核の周りを安定に回る定常状態となる(量子条件)
・エネルギー$E_m$の定常状態にある電子が別のエネルギー$E_n$の定常状態に移るとき、$h\nu=E_n-E_m$ のエネルギーの光子を放射あるいは吸収する(振動数条件)
● ● ●
ボーアの量子仮説に基づけば定常状態のエネルギーを数式から求めることができる。こうしてエネルギー準位の概念が創出され、これによって原子半径や水素原子の輝線スペクトルを説明するリュードベリの公式を導出することができる。
量子理論ではこれまで連続と思われてきたエネルギーという物理量を量子化する、という大胆な発想によって様々な物理的現象を構成、説明することに成功してきた。
しかし、多電子原子の輝線スペクトルや化学結合をうまく説明することはできなかった。また、本質的になぜ整数が導入されなければならないのかという疑問に対する理論的な説明は省かれていた。
このような言わば天下り的な導出に基づく理論的に発展途上の量子論は「前期量子論」と呼ばれる。
それから約10年後の1926年、世に名高いシュレディンガー方程式が物理学界を席巻することになる。
