4.2 不等式の利用
不等式が絞り込みに利用できる場面にはある程度パターンがあります。列挙しておきます。
(この他のパターンも色々と挙げられますが、これら3つは考え方が特に重要なので是非マスターしましょう)
1.指数 Vs 多項式
難関大入試でよく出題されているパターンです。この型に慣れておけば、得点源間違いなしです。
着眼点はズバリ「オーダー」です。「オーダー」とは大雑把に言えば「大きさ」のことで、2つ以上の数について、どのくらい大きくなるのかを比較するときに用いる数学用語です。
指数関数は多項式関数に比べて非常に速く増加します。このことを利用して等式の成り立つポイントを探るのがこのパターンの攻略法です。
解答例
$n \geqq 4$ のとき、$n^2<2^n+1$を数学的帰納法により示す。
$n=4$のとき、(左辺)$=16$、(右辺)$=17$より、成立。
$n=k \ (k \geqq 5)$のとき、$k^2<2^k+1$の成立を仮定すると、$$\begin{align} 2^{k+1}+1-(k+1)^2 &= 2 \cdot 2^k – (k^2+2k) \\ &> 2(k^2-1)-(k^2+2k) \\ &= k^2-2k-2 \\ &= (k-1)^2-3 \end{align}$$となる。$k \geqq 5$のとき$ (k-1)^2-3 >0$だから、$n=k+1$のときでも成立する。
以上より、数学的帰納法から$n \geqq 4$のとき、$n^2<2^n+1$であることが言えるから、可能な$n$は$1,2,3$に限られる。このうち$n^2=2^n+1$を満たすような$n$は$n=3$のみであるから、求める自然数$n$は$$\color{red}{n=3} \ \cdots \cdots (\text{答})$$である。
以上は典型題ですが、こうした問題は頻繁に出題されているので、よく練習しておきましょう。
2.分数式
絞り込みと言えばこのタイプを思い浮かべる人も多いのではないでしょうか。
分数式パターンも指数 Vs 多項式パターンと同様に着眼点は大小関係ですが、こちらの場合は自分で適切に大小関係を持ち出すところがポイントです。
解答例
与式は$a、b$について対称だから$a \leqq b$と設定しても一般性は失われない。(←これが重要!)
これより$\dfrac{1}{a} \geqq \dfrac{1}{b}$であるから、$$\dfrac{1}{a}+\dfrac{1}{b} = \dfrac{1}{2}$$ $$\therefore \dfrac{1}{a}+\dfrac{1}{a} \geqq \dfrac{1}{2}$$ $$\therefore \dfrac{2}{a} \geqq \dfrac{1}{2}$$ $$\therefore a \leqq 4 $$となる。故に可能な$a$の値は$1,2,3,4$である。
$a=1$のとき、与式の左辺は$1$より大きくなるが、右辺は$1$より小さいので不適。
$a=2$のとき、与式の左辺は$\dfrac{1}{2}$となり、与式は$\dfrac{1}{b}=0$と変形できるが、このような$b$は存在しないので不適。
$a=3$のとき、与式は$\dfrac{1}{b}=\dfrac{1}{6}$と変形できる。故に$(a,b)=(3,6)$を得る。
$a=4$のとき、与式は$\dfrac{1}{b}=\dfrac{1}{4}$と変形できる。故に$(a,b)=(4,4)$を得る。
$a \geqq b$とすれば全く同様に$(a,b)=(4,4)、(6,3)$を得るから、以上により、求める$a、b$の組は$$\color{red}{(a,b)=(3,6)、(4,4)、(6,3)} \ \cdots \cdots (\text{答})$$である。
上記の例題は数え上げるタイプの典型題です。このタイプの整数問題も頻出です。条件式がすべての文字について対称であるときは、文字の大小を自分で勝手に設定しても解の一般性が保たれるので、最後に大小の制限を外せばOKです。自分で大小を設定した方が解答しやすい問題も多く出題されていますから、こうした手法に慣れておきましょう。
これとは別のタイプの分数特有の条件を使う問題を見てみましょう。
分数式が整数になるということは分子が分母で割り切れなければなりません。ここで(分子)≧(分母)という大小関係が必要条件として出てきます。この不等式から解を求めます。
解答例
分数が整数となるためには分子が分母より大きいことが必要である。故に$2x \geqq y^2+1、2y \geqq x^2+1$が必要である。これらより、$$\begin{align} \left( \dfrac{y^2+1}{2} \right)^2+1 & \leqq 2y \\ \therefore y^4+2y^2+5 & \leqq 8y \\ \therefore y^4+2y^2-8y+5 & \leqq 0 \\ \therefore (y-1)^2 (y^2+2y+5) & \leqq 0 \\ \therefore y &= 1 \end{align}$$となる。よって$2 \geqq x^2+1$より、$x=1$を得る。
また、$(x,y)=(1,1)$のとき$\dfrac{2x}{y^2+1}$、$\dfrac{2y}{x^2+1}$はともに整数となるから題意に適する。
以上より、求める$x、y$の組は$$\color{red}{(x,y)=(1,1)} \ \cdots \cdots (\text{答})$$である。
「分子が分母より大きい」というのは言われてしまえば何ということも無い条件ですが、意外に盲点だったりします。特に分数式を扱っているという意識のない時に見落としがちな条件です。
最後にもう一つ、分数式パターンで頻出の例題を紹介しましょう。
このタイプの分数式でまずやるべきことは分子の「次数下げ」です。
解答例
分母は$0$でないから $n+1 \ne 0 \iff n \ne -1$ である。
与式は$$\dfrac{n^2+4n+5}{n+1}=n+3+\dfrac{2}{n+1}$$と変形できる。$n+3$は整数だから、与式が整数となるためには$\dfrac{2}{n+1}$が整数となる必要がある。よって$n+1$は$2$を割り切らなければならないから、$n+1=\pm 1 , \pm 2$ が必要である。よって $n=-3,-2,0,1$ を得る。
$n=-3,-2,0,1$のとき与式はそれぞれ $-1,-1,5,5$ となり整数となるから題意に適する。
以上より、求める整数$n$は$$\color{red}{n=-3,-2,0,1} \ \cdots \cdots (\text{答})$$である。
このタイプの問題はほとんどワンパターンなので類題を経験しておくだけでも大きなアドバンテージとなります。
3.隣接整数
このタイプは大学入試ではあまり見られません。もし出題されても大抵の場合は誘導が付きます。具体的に言うと「整数$n$と$n+2$の間にある整数は$n+1$である」ということを利用します。…これだけ聞くと何を当たり前のことを言っているんだと思われるかもしれませんが、このことに気付かないと延々と時間ばかりが過ぎていく問題も出題されています。仕組みと解き方くらいは理解しておきしましょう。
解答例
$$\begin{align}& \ \ \ \ \ (4n^2+n-3)-(2n-1)^2 \\ &=5n-4 \\ &>0 \end{align}$$および、$$\begin{align}& \ \ \ \ \ (2n+1)^2-(4n^2+n-3) \\ &=3n+4 \\ &>0 \end{align}$$より、$$(2n-1)^2 < 4n^2+n-3 < (2n+1)^2$$が成立する。よって、$4n^2+n-3$が平方数となるためには$4n^2+n-3=(2n)^2$が必要であるから、これを解いて$n=3$を得る。
また、$n=3$を $4n^2+n-3$ に代入すると$36$となり、確かに平方数となっている。
以上より、求める自然数$n$は$$\color{red}{n=3} \ \cdots \cdots (\text{答})$$である。
こういった問題を解く際には、「整数で挟む意識」が大切です。
この場合は $4n^2+n-3=N^2$ などと置いて$$n-3=(N-2n)(N+2n)$$と変形しても一向に解決の糸口が掴めませんが、不等関係を見つけようと常に意識していれば、$4n^2$に近い平方数で挟めるんじゃないか?と一歩前進できます。実際、$(2n-1)^2$や$(2n+1)^2$を持ち出しているのはこうした考察に基づいています。ここでも「オーダー」の視点が役に立ちますね。
逆に考えれば、$4n^2+n-3=N^2$などと置いてもダメな場合は「もしかして挟むタイプか?」と勘ぐることができるとも言えます。何にせよ「整数で挟む意識」があれば、この例題のように誘導設問がカットされていても正答に辿り着くことができるはずです。
隣接整数タイプではもう一つ重要な概念が登場します。
そうです。皆さんが大好きな「ガウス記号」ですね(笑)。
個人的な推測ですが、ガウス記号の苦手な人が多い理由は恐らく単に慣れてないからだと思います。ガウス記号は離散的な値を表すためなかなか取っ付きにくいということもあり、入試の現場では出来不出来を大きく左右しかねない存在です。
ガウス記号の定義は以下のようなものでしたね。
《ガウス記号の定義》
実数$x$に対して、$[x]$は$x$を超えない最大の整数を表す。
これだけです。これだけなんですが、負の数を考えたりすると頭の中がこんがらがる人が続出します…。
不等式で表すと、以下のようになります。
実数$x$に対して、$[x]$は$$[x] \leqq x < [x]+1$$を満たす。
要するに、実数$x$の小数部分を切り捨てた数を$[x]$と表しているということです。ですから小数部分がゼロのとき、つまり$x$が整数のときは切り捨て後も$x$ですから、$[x]=x$です。こういう得体の知れない記号が出てきたときはまず具体例で考えることが大切です。
例えば、$[8.61]=8$、$[\pi]=3$、$[2]=2$となります。
負の数の場合は絶対値が大きくなるので混乱しやすいのですが、定義の不等式を変形すると、$$x-1 < [x] \leqq x$$となるので、$[-8.61]=-9$、$[-\pi]=-4$、$[-2]=-2$となります。
ガウス記号 $y=[x]$ のグラフは以下のようになります。
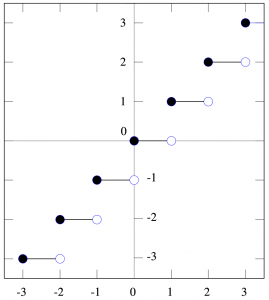
黒丸が数直線の小さい方、底にあるという特徴から、ガウス記号は「床関数」(floor function)とも呼ばれています。このグラフは頭に入れておきたいですね。確かに $x-1 < [x] \leqq x$ が成立していることも分かります。
床関数があるなら「天井関数」もあるのではと思われた方、鋭いですね。もちろん存在しますが、あまり需要が無いのでここでは割愛します。興味のある人は調べてみてください。
さて、このガウス記号ですが、入試にはそこそこ出てきます。整数分野が絡むと結構難しめの問題に仕上がってしまうので、今は簡単な問題で練習しましょう。
解答例
ガウス記号の定義より、$\left[ \dfrac{n}{2} \right] \leqq \dfrac{n}{2}$となるから、与式の右辺について、$n^2-1 \leqq \dfrac{n}{2}$が必要である。これを解くと$$\dfrac{1-\sqrt{17}}{4} \leqq n \leqq \dfrac{1+\sqrt{17}}{4}$$を得る。$n$は整数だから、$n=0、1$に限られる。
$n=0$のとき、$\left[ \dfrac{n}{2} \right]=0$、$n^2-1=-1$となり不適。
$n=1$のとき、$\left[ \dfrac{n}{2} \right]=0$、$n^2-1=0$となり適する。
以上より求める整数$n$は$$\color{red}{n=1} \ \cdots \cdots (\text{答})$$である。
実際に出題されている問題はこんなに可愛いものではありませんが、不等式を利用する、もしくはガウス記号を整数($N$などの形)に置き換えてしまうなどのアプローチが基本となります。
このように不等式は答えを求める道具であると同時に、解答を書く労力を軽減する役割も持っています。不等式は「答え以外の余計なものを削ぎ落とす道具だ」という感覚で使って下さい。
不等式を作り出すということは大小関係を設定するということです。対称性を持つ条件が与えられたとき、あえてその対称性を崩した方が答えに辿り着きやすくなることがあります。
