回転体の求積問題
ここでは座標計算をあまり要さない「ナチュラルな回転体」の問題を蒐集するよう心掛けています。ただし面白い関数の回転体に関するユニークな出題であれば、その限りではありません。
関数の回転体
・三角関数の回転体に関する問題
岐阜大学(2003年/理系第3問)
$xy$平面上の2つの曲線 $y=\cos \dfrac{x}{2}\ (0 \leqq x \leqq \pi)$ と $y=\cos x\ (0 \leqq x \leqq \pi)$ を考える。以下の問に答えよ。
(1)上の2つの曲線、および直線 $x=\pi$ を描き、これらで囲まれる領域を斜線で示せ。
(2)(1)で示した斜線部の領域を$x$軸のまわりに1回転して得られる回転体の体積を求めよ。
・サイクロイドの回転体に関する問題
北九州市立大学(2017年/(国際環境工)第3問)
・カージオイドの回転体に関する問題
名古屋市立大学(2011年/(芸術工)第4問)
その他の関数の回転体
東京大学(1989年/第5問)
※$\pi x^2 \sin \pi x$の回転体。誘導として「バウムクーヘン分割」による積分公式の導出が課されています。
(類題:気象大学校(1980)、筑波大学(1993)など)
東京都立大学(1996年/(人文/経済)第3問)
$n$を自然数とし、二つの曲線 $y=x^n$、$y^2=x$ によって囲まれる図形を$F$とする。
(1)$F$の面積を求めよ。
(2)$F$を$x$軸のまわりに一回転してできる立体の体積$V$を求めよ。
(3)$F$を$y$軸のまわりに一回転してできる立体の体積$V$を求めよ。
東京工業大学(2015年/第3問)
※$e^{-x^2}$の回転体。(大学教養レベルの数学では重積分の範囲で登場します)
慶應義塾大学(2020年/(医)第1問(2))
※ $f(x)=\dfrac{\log x}{\sqrt{x}}(x>0)$ の回転体。
京都大学(2020年/前期理系第6問)
※ $z=\sqrt{\log (1+x)}$ $(0 \leqq x \leqq 1)$ の回転体。
関西学院大学(2021年全学部日程(2/1)/理系第4問)
関数$f(x)$と$g(x)$を$$f(a)= ax^2+bx-1、\ g(x) =c\log a$$
とし、曲線$C_1$と$C_2$を、$$C_1:y=f(a)、\ C_2:y=g(x)\ (x>0)$$とする。ただし、$a$、$b$、$c$は実数の定数で、$a\ne 0$、$c>0$ とする。また、曲線$C_1$と曲線$C_2$は共有点$(1,\,0)$をもち、その点で共通の接線$\ell$をもつとする。さらに、曲線$C_1$と曲線$C_2$および直線 $x=2$ で囲まれた部分を$D$とする。次の問いに答えよ。
(1)定数$a$、$b$を$c$のみを用いて表せ。
(2)定積分 $\small \displaystyle\int_{1}^{2} \log x d x$ および $\small \displaystyle\int_{1}^{2}(\log x)^{2} d x$ の値を求めよ。
(3)$D$の面積$S$が $\small S=\dfrac{10}{3}-4 \log 2$ であるとする。このとき、$c$の値および直線$\ell$の方程式を求めよ。
(4)$c$が(3)で求めた値をとるとき、$D$を軸の周りに1回転させてできる立体の体積$V$を求めよ。
正四面体の回転体
東大実戦(2013年/第2回理系(駿台))
※首都大学東京(2014年/後期)と同じ題意の問題。ただし回転させるのは正四面体の「表面」です。(著作権の関係で問題文の掲載は控えさせて頂きます)
首都大学東京(2014年/後期(都市教養,都市環境,システムデザイン)第4問)
一辺の長さが$\sqrt{2}$の正四面体$OABC$の辺$OA$、$BC$の中点をそれぞれ$M$、$N$とし、$0<t<1$ に対して線分$MN$を$t:1−t$に内分する点を$P$とする。以下の問いに答えなさい。
(1)$MN$の長さを求めなさい。
(2)辺$OC$上の$1$点$Q$は$MN$と$PQ$が直交するように定められているとする。$OQ$の長さを求めなさい。
(3)$MN$を軸として正四面体$OABC$を$1$回転させてできる回転体の体積を求めなさい。
立方体の回転体
東京工業大学(1993年/後期第1問)
一辺の長さが$1$の立方体を、中心を通る対角線のうちの一本を軸として回転させたとき、この立方体が通過する部分の体積を求めよ。
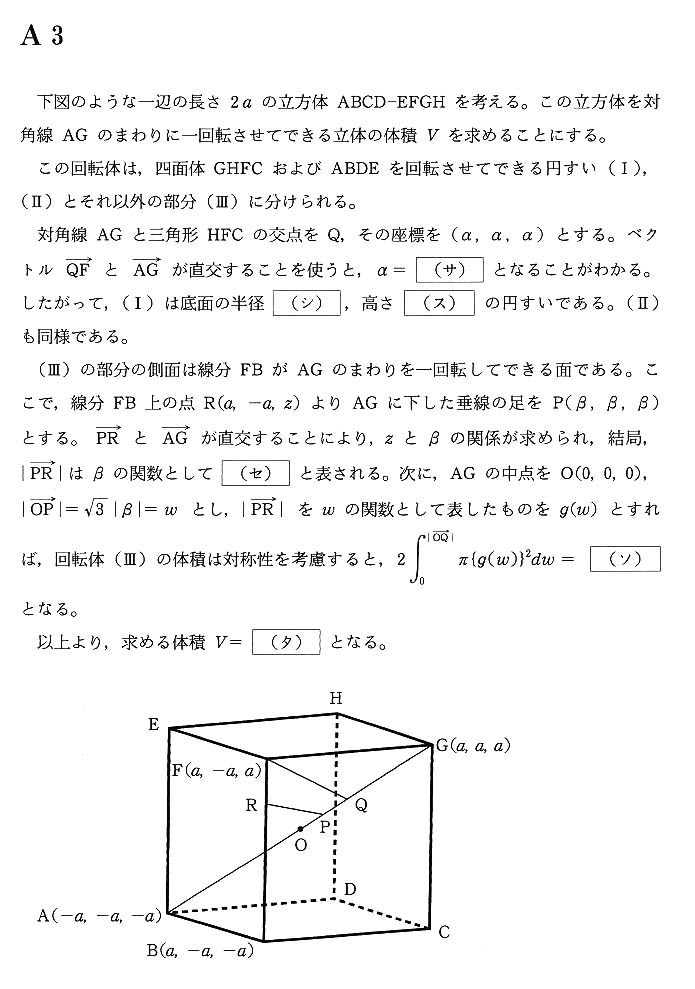
慶應義塾大学(1998年/(理工)第3問)
京都大学(2010年/文系第5問)
※体対角線周りの回転体
東京理科大学(2018年/(理)第2問)

正八面体の回転体
東京大学(1990年/理科第3問)
(求積問題ではないですが正八面体の断面図を必要とする珍しい出題なのでここに掲載しておきます)
東京大学(2008年/理科第3問)
(1)正八面体のひとつの面を下にして水平な台の上に置く。この八面体を真上から見た図(平面図)を描け。
(2)正八面体の互いに平行な2つの面をとり、それぞれの面の重心を $\mathrm{G_1}$、$\mathrm{G_2}$ とする。$\mathrm{G_1}$、$\mathrm{G_2}$ を通る直線を軸としてこの八面体を1回転させてできる立体の体積を求めよ。ただし八面体は内部も含むものとし、各辺の長さは$1$とする。
その他の図形の回転体や軸対称領域
東京大学(2002年/理科第3問)
$xyz$空間内の原点$O(0,0,0)$を中心とし、点$A(0,0,−1)$を通る球面を$S$とする。$S$の外側にある点$P(x,y,z)$に対し、$OP$を直径とする球面と$S$との交わりとして得られる円を含む平面を$L$とする。点$P$と点$A$から平面$L$へ下ろした垂線の足をそれぞれ$Q、R$とする。このとき、$PQ \leqq AR$であるような点$P$の動く範囲$V$を求め、$V$の体積は$10$より小さいことを示せ。
東京大学(2016年/理科第6問)
座標空間内を、長さ$2$の線分$\mathrm{AB}$が次の2条件(a)、(b)をみたしながら動く。
(a) 点$\mathrm{A}$は平面 $z=0$ 上にある。
(b) 点$\mathrm{C}(0,0,1)$が線分$\mathrm{AB}$上にある。
このとき、線分$\mathrm{AB}$が通過することのできる範囲を$K$とする。$K$と不等式 $z \geqq 1$ の表す範囲との共通部分の体積を求めよ。
大阪大学(2020年/第5問)

回転体に内接する図形の求積
慶應義塾大学(2021年/(環境情報)第5問)
