具体的な運動の解析に入る前に、運動にはどういう要素があるのかを復習しておきましょう。ここでは物体の変位と速度について復習します。「微分」という重要な数学的操作についても簡単に説明します。
変位=位置の変化量
力学で物体の運動を追跡する際は、物体の位置がどのくらい変化したのかを調べる必要があります。その際に用いられるのが「変位」と呼ばれる物理量です。
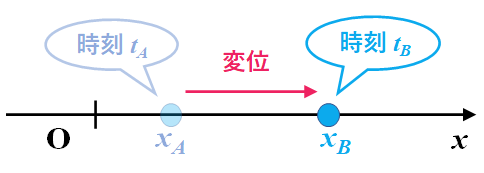 図.1次元座標における変位
図.1次元座標における変位
変位とは位置の変化量を表し、正の値も取れば負の値も取ります。より具体的には、時刻$t_A$と$t_B$の間における位置の変化量$\Delta x$を変位と定義しています。式で表すと次のようになります。$$\Delta x=x(t_A)-x(t_B) \tag{1}$$さて、ここで重要なポイントが2つあります。
1点目は、物体の位置が「$x(t)$」のように時刻$t$の関数として表せるという点です。例えば$x(t_A)$は時刻$t_A$における位置を表し、$x(t_B)$は時刻$t_B$における位置を表しています。これは、時刻$t$を変数とするある関数$x(t)$があって、これに $t=t_A$ などの値を代入したものと見なすことができます。このように、ニュートン力学の根幹には
「時刻を決めれば物体の位置が決まる」
という性質が横たわっているのです。あまりにも当たり前すぎて、誰も改めてマジメに考えることのない事実なのですが、これはとても重要な性質です。
2点目は、変位$\Delta x$が「大きさ」と「向き」を持った量、つまりベクトル量であるという点です。ある点の位置を決めるためには、必ず基準からの距離、あるいは方向や角度を定めなければなりません。これはすなわち、
「物体の位置はベクトルで与えられる」
ということを意味しています。位置はベクトルで与えられるので、その差分である変位もまたベクトルで与えられます。
力学的な運動を解析する上で重要な要素は「位置」と「時刻」です。「位置が時刻の(ベクトルの)関数になる」という考え方は、これから力学を学ぶ上での基礎となります。
速度=単位時間あたりの変位
変位をその間の時間間隔$\Delta t$で割った量、すなわち単位時間あたりの平均の変位を「平均の速度」$\bar{v}$といいます。式にすると次のようになります。$$\bar{v}=\dfrac{\Delta x}{\Delta t}=\dfrac{x(t+\Delta t)-x(t)}{\Delta t} \tag{2}$$ここで$\Delta x$は変位なのでベクトル量です。つまり「速度」もまたベクトル量であり、大きさだけではなく向きも成分として含みます。これに対して、「速さ」は速度から「向き」の成分を除いた「大きさ」のみを値とするスカラー量を指します。「速度の絶対値$|v|$が速さである」という認識でも良いでしょう。両者は混同されやすいので、しっかり区別を付けて下さい。
速度 ・・・ ベクトル量(向き+大きさ)
速さ ・・・ スカラー量(大きさ)
※ベクトルは別名「有向線分」と呼ばれる量で「向き」という要素も含んでいます。日常会話でも「あの人は努力のベクトルがズレてるよね…」とか「意識のベクトルを外に向けましょう」とか言ったりします。
※日常生活レベルでは「速度」と「速さ」を厳密に使い分ける人は多くありませんが、物理の世界では厳密に区別されます。例えば、質量、長さ、エネルギー、電荷、温度などはスカラー量です。「でも電荷はプラスマイナスがあるからベクトルなんじゃないの?」と思われた方はなかなか鋭いですね! 実は、スカラーには「座標系に依存しないこと」が要請されています。つまり、止まっている人から見ても、動いている人から見ても、同じ量として観測されるものがスカラーなのです。確かに、プラスマイナスを考えれば電荷を1次元のベクトルと見なすことも可能ですが、+1の電荷は止まっている人から見ても、動いている人から見ても同じ+1の量として観測されます。この判断基準に照らせば電荷がスカラー量であることは明らかですよね。
力学では「瞬間の速度」が重要
「変位」と「速度」という2つの重要な概念について紹介しました。
上で述べた通り、ある時間$\Delta t$に対して平均の速度$\bar{v}$が定義できますが、実はこれはあまり実用的ではありません。
例えば、自動車の運転を想像してみて下さい。車を運転していると、気持ちよく走っている時もあれば、赤信号に止められている時もあって、ドライブ中のスピードはまちまちで一定ではありませんよね。もしスピードメーターに平均の速度しか表示されなかったらどうなるでしょうか? いま車がどのくらいのスピードで走行しているのかが全く分からないことになってしまいます。これはとてもキケン⚠です!
・・・というのは極端な例ですが、何を伝えたいのかと言うと物体の運動を解析するには「瞬間の速度」が重要であるということです。
瞬間の速度を求める
ここでちょっとした微分学の出番です。点$\mathrm{P}$の位置が時刻$t$の関数$x(t)$で表されるとします。平均の速度の定義式$$\bar{v}=\dfrac{\Delta x}{\Delta t}=\dfrac{x(t+\Delta t)-x(t)}{\Delta t} \tag{2}$$において、$\Delta t$ をどんどん小さくしていくと、ベクトルの向き(平均の速度)がどんどん点$\mathrm{P}$での接線の傾きに近付いていきます。$\Delta t$ を極限までゼロに近づけると、接線(灰色の直線)の方向に一致しそうですよね。実はこの操作こそが「微分」と呼ばれている数学的操作そのものに相当しています。
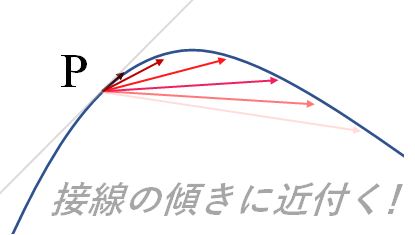 図.ベクトルの向きが接線方向に近付く
図.ベクトルの向きが接線方向に近付く
マジメに数式で書くと次のようになります。$$\displaystyle v=\lim _{\Delta t \to 0} \dfrac{x(t+\Delta t)-x(t)}{\Delta t}=\dfrac{\mathrm{d}}{\mathrm{d}t} x(t) \tag{3}$$ $(2)$式と対応させてみると、これは時刻$t$ちょうどでの関数$x(t)$の接線の傾きを表しています。この傾きこそが「瞬間の速度」$v$ です。
ここで、$(3)$式の$\displaystyle \lim _{\Delta t \to 0}$は「$\Delta t$の値を限りなく$0$に近づけますよ~」ということを表しています。また、$\dfrac{\mathrm{d}}{\mathrm{d}t} x(t)$ という式は「関数$x(t)$を変数$t$で微分しますよ~」ということを表しています。微分することを簡潔に表しただけだと考えて下さい。
時刻$t$における速度
要するに、時刻$t$における位置を表す関数$x(t)$があったときに、関数$x(t)$を微分したもの(関数$x(t)$の傾き)が時刻$t$における速度になります。位置$x$が時刻$t$の関数なのですから、当然速度も時刻$t$の関数$v(t)$として表現できるはずです。
例えば、ある点$\mathrm{P}$の時刻$t$における位置が $x(t)=t^2$ と表せたとしましょう。このとき、時刻$t$における速度$v(t)$は定義式である$(3)$式を用いて次のように計算できます。$\lim$の計算を習っていない方は眺めるだけで構いませんが、こういう風に計算するのだと知っておくと後々役に立つかもしれません。$\require{cancel}$ $$\begin{align} \displaystyle v &=\lim _{\Delta t \to 0} \dfrac{x(t+\Delta t)-x(t)}{\Delta t} \\ &=\lim _{\Delta t \to 0} \dfrac{(t+\Delta t)^2-t^2}{\Delta t} \quad (x(t)=t^2\text{ を代入}) \\ &=\lim _{\Delta t \to 0} \dfrac{t^2+2t(\Delta t)+(\Delta t)^2-t^2}{\Delta t} \\ &=\lim _{\Delta t \to 0} \dfrac{2t\cancel{(\Delta t)}+\cancel{(\Delta t)}^2}{\cancel{\Delta t}} \\ &=\lim _{\Delta t \to 0} (2t+\Delta t) \\ &=2t+0 \\ &=2t \quad (\text{←これが時刻}t\text{での速度の関数!}) \end{align}$$よって、$x(t)=t^2$ という式で位置を表現できる運動をする点$\mathrm{P}$について、時刻$t$における速度$v(t)$は$$v(t)=2t$$で与えられることが分かります。これでどんな時刻の速度でも時刻$t$を代入するだけで求められますから、物理学の目標である「未来の予言」に一歩近付くことができました。
(おまけ)多項式の微分公式
どうでしたか? 物体の位置を時刻の関数で表すことができれば、速度も求めることができるのです。とても面白いですよね!
ただし普段、力学の問題を解く際はいちいち定義に従って関数を微分したりしません。なぜなら、便利な微分公式があるからです。
この公式に従って計算すれば関数を簡単に微分することができます。高校では数学Ⅱの範囲の知識なので初めて見た人はよく分からないかもしれませんが、例えば$$t^3+4t^2+3t+9$$という関数を$t$で微分すると$$3t^2+8t+3$$になります。このように上の公式を使えば微分の定義を考えなくて済むので、すぐに求めることができます。
微分の計算をいちいち定義に従って進めるのは面倒、という訳で公式が活躍します。是非覚えておきましょう!
