有限の高さの矩形ポテンシャルとトンネル効果
有限の高さの矩形ポテンシャル
シュレーディンガー方程式の詳細については前節までの内容を参照されたい。ここでは空間内に有限の高さをもつ矩形ポテンシャルが存在する系について考察する。
想定されるポテンシャルは次のようなものである。
これに対して $x$ 方向 $-\infty$ から正の向きに粒子が入射した場合について考えてみよう。
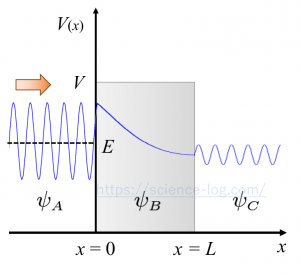
このとき、波動関数は3つの領域について考える必要がある。なぜなら、$x<0$、$0 \leqq x \leqq L$、$L<x$ の3つの領域に分けてシュレーディンガー方程式を考えなければならないからである。これらをそれぞれ領域A、領域B、領域Cとしよう。いま、ポテンシャル$V(x)$は$$\small V(x)=\left\{\begin{array}{ll}
0 & (x < 0) \\
V>0 & (0 \leqq x \leqq L) \\
0 & (x > L)
\end{array}\right.\tag{4.1}$$となっている。
質量$m$の粒子の1次元の運動を記述するシュレーディンガー方程式は前頁で確認した$(2.2)$式の通りに表されるから、領域Aにおけるシュレーディンガー方程式は$$\small \left[-\dfrac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}\right] \psi_{A}(x)=E \psi_{A}(x) \tag{4.2a}$$となる。
領域Bには有限のポテンシャル$V$が存在するから、$$\small \left[-\dfrac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}+V\right] \psi_{B}(x)=E \psi_{B}(x) \tag{4.2b}$$となる。
領域Cでは $V(x)=0$ なので$$\small \left[-\dfrac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}\right] \psi_{C}(x)=\psi_{C}(x) \tag{4.2c}$$となる。
シュレーディンガー方程式を解く
シュレーディンガー方程式はほとんどの場合、解析的に解くことはできないということを前頁で述べた。しかし、適当な条件を与えれば例外的に解くことができることがある。
$E>V$ のとき
$(4.2)$の各方程式の形の場合、解となる波動関数は以下のように求められる。$$\small \begin{array}{ll}
\psi_{A}(x)=A_{+} \mathrm{e}^{i k_{1} x}+A_{-} \mathrm{e}^{-i k_{1} x} & (x<0) \\
\psi_{B}(x)=B_{+} \mathrm{e}^{ik_{2} x}+B_{-} \mathrm{e}^{-ik_{2} x} & (0 \leqq x \leqq L) \\
\psi_{C}(x)=C_{+} \mathrm{e}^{i k_{1} x} & (L<x)
\end{array} \tag{5.1}$$式中の$A_{+}$などは係数である。
ここで、$x$方向正の向きに進む粒子は$\mathrm{e}^{i k_{1} x}$、$\mathrm{e}^{i k_{2} x}$の項で表現され、負の向きに進む粒子は$\mathrm{e}^{-i k_{1} x}$、$\mathrm{e}^{-i k_{2} x}$の項で表現されている。なお、$\psi_{C}(x)$の式に指数が負の項が含まれていないのは、領域Bを通過した後の領域Cに存在する粒子は$x$方向正の向きに進むものしか考慮していないためである。粒子は各領域の境界で部分的に反射し、一部は透過する。そのため領域Aと領域Bでは負の向きに進行する粒子を無視できないのである。一方で領域Cから領域Bに侵入する粒子は存在しないので考える必要は無い。
さて、$(4.3)$の各係数を求めるのであるが、これには境界において各関数が滑らかに接続されている、という条件に基づいて求められる。領域AとBの境界においては、
$\psi_{A}(0)=\psi_{B}(0)$ および $\psi_{A}^{\prime}(0)=\psi_{B}^{\prime}(0)$
という条件を考慮し、領域BとCの境界においては、
$\psi_{B}(0)=\psi_{C}(0)$ および $\psi_{B}^{\prime}(0)=\psi_{C}^{\prime}(0)$
という条件を考慮する。これは境界において波動関数が「連続かつ微分可能」であるための必要十分条件になっている。
これより、$x=0$ として$$\small \begin{cases} A_{+}+A_{-}=B_{+}+B_{-} \\ k_1 A_{+}+k_1 A_{-}=k_2 B_{+}+k_2 B_{-} \end{cases} \tag{5.2}$$を得る。同様に $x=L$ として$$\small \begin{cases} B_{+} e^{i k_{2}L}+B_{-} e^{-i k_{2}L} =C_{+} e^{i k_{1}L} \\ k_{2}\left(B_{+} e^{i k_{2}L}-B_{-} e^{-i k_{2}L}\right) =k_{1} C_{+} e^{i k_{1}L} \end{cases} \tag{5.3}$$を得る。
いま、$A_{+}$、$A_{-}$、$B_{+}$、$B_{-}$、$C_{+}$ の5つの未知数に対して方程式は4つなので、いずれか一つの文字は消去できずに残る。そこで$C_{+}$を残し、他の文字を$C_{+}$を使って表すことにする。
$(5.3)$より、$$\small \begin{array}{l}
B_{+}=\dfrac{k_{1}+k_{2}}{2 k_{2}} e^{i\left(k_{1}-k_{2}\right) L} C_{+} \\
B_{-}=\dfrac{k_{2}-k_{1}}{2 k_{2}} e^{i\left(k_{1}+k_{2}\right) L} C_{+}
\end{array} \tag{5.4}$$を得る。また、$(5.2)$より、$$\small \begin{array}{l}
A_{+}=\dfrac{\left(k_{1}+k_{2}\right) B_{+}+\left(k_{1}-k_{2}\right) B_{-}}{2 k_{2}} \\
A_{-}=\dfrac{\left(k_{1}-k_{2}\right) B_{+}+\left(k_{1}+k_{2}\right) B_{-}}{2 k_{1}}
\end{array} \tag{5.5}$$となるので、$(5.4)$を代入して頑張って整理すると$$\small \begin{array}{l}
A_{+}=\left\{\cos \left(k_{2}L\right)-i \dfrac{k_{1}^{2}+k_{2}^{2}}{2 k_{1} k_{2}} \sin \left(k_{2}L\right)\right\} e^{i k_{1}L} C_{+} \\
A_{-}=i \dfrac{k_{1}^{2}-k_{2}^{2}}{2 k_{1} k_{2}} \sin \left(k_{2}L\right) e^{i k_{1}L} C_{+}
\end{array} \tag{5.6}$$となる。なお、式変形で $\sin x=\dfrac{e^{-ix}-e^{ix}}{2i}$、$\cos x=\dfrac{e^{-ix}+e^{ix}}{2}$ の関係を用いている。
なお、$k_1=\dfrac{\sqrt{2mE}}{\hbar}$、$k_2=\dfrac{\sqrt{2m(E-V)}}{\hbar}$ である。
$E<V$ のとき
基本的には $E>V$ のときと解き方は変わらないが、領域Bにおける波動関数が異なり、解となる波動関数は以下のように求められる。$$\small \begin{array}{ll}
\psi_{A}(x)=A_{+} \mathrm{e}^{i k_{1} x}+A_{-} \mathrm{e}^{-i k_{1} x} & (x<0) \\
\psi_{B}(x)=B_{+} \mathrm{e}^{\color{red}{k_{2} x}}+B_{-} \mathrm{e}^{\color{red}{-k_{2} x}} & (0 \leqq x \leqq L) \\
\psi_{C}(x)=C_{+} \mathrm{e}^{i k_{1} x} & (L<x)
\end{array} \tag{5.7}$$これは $E>V$ のときの結果に対して $ik_2$ を $k_2$ に置き換えればよい。また、$E<V$ のときは、$k_1=\dfrac{\sqrt{2mE}}{\hbar}$ は値が変わらず、$k_2$の中身の式が変わって $k_2=\dfrac{\sqrt{2m(V-E)}}{\hbar}$ となる。これを代入すれば $E<V$ のときの式が得られる。
なお、このとき$\psi_{B}(x)$は複素関数ではなく減衰する指数関数となるので、計算して確かめておこう($(5.7)$の$\psi_{B}(x)$の式が実数関数になっていることに注意)。
反射率と透過率
$x$ 方向 $-\infty$ から正の向きに入射した粒子の反射率$R$および透過率$T$を求めてみると、以下のようになる。
$E>V$ のとき
$$\small \begin{align}
R &= \dfrac{|A_{-}|^{2}}{|A_{+}|^{2}} \\
&=\dfrac{\left(k_{2}^{2}-k_{1}^{2}\right)^{2} \sin ^{2}\left(k_{2}L\right)}{4 k_{1}^{2} k_{2}^{2}+\left(k_{1}^{2}-k_{2}^{2}\right)^{2} \sin ^{2}\left(k_{2}L\right)} \\
&=\dfrac{V^{2} \sin ^{2}\left(k_{2}L\right)}{4 E\left(E-V\right)+V^{2} \sin ^{2}\left(k_{2}L\right)} \tag{6.1}
\end{align}$$ $$\small \begin{align}
T &= \dfrac{|C_{+}|^{2}}{|A_{+}|^{2}} \\
&=\frac{4 k_{1}^{2} k_{2}^{2}}{4 k_{1}^{2} k_{2}^{2}+\left(k_{1}^{2}-k_{2}^{2}\right)^{2} \sin ^{2}\left(k_{2}L\right)} \\
&=\frac{4 E\left(E-V\right)}{4 E\left(E-V\right)+V^{2} \sin ^{2}\left(k_{2}L\right)} \tag{6.2}
\end{align}$$
前頁で確認したように、波動関数の絶対値の2乗が粒子の存在確率を表す、というのが量子力学の確率解釈であった。これにしたがって、比は波動関数の絶対値の2乗に対して取ることになる。反射率$R$は障壁に接触後に負方向に戻る粒子が観測される確率を表し、透過率$T$は障壁を通り抜けて領域Cで粒子が観測される確率を表している。また、反射率と透過率について、$$R+T=1$$の関係式が成り立つが、これは粒子の存在確率の総和を考えると自明なことと言える。
反射率が有限値を取ることから、$E>V$ の場合であっても粒子は壁を完全に通り抜けはせず一部は反射されることが分かる。これは古典物理と大きく異なる点である。
$E<V$ のとき
反射率$R$および透過率$T$はそれぞれ以下のようになる。$$\small \begin{align}
R &= \dfrac{|A_{-}|^{2}}{|A_{+}|^{2}} \\
&=\dfrac{\left(k_{1}^{2}+k_{2}^{2}\right)^{2} \sinh ^{2}\left(k_{2} L\right)}{4 k_{1}^{2}k_{2}^{2}+\left(k_{1}^{2}+k_{2}^{2}\right)^{2} \sinh ^{2}\left(k_{2} L\right)} \\
&=\dfrac{V^{2} \sinh ^{2}\left(k_{2} L\right)}{4 E\left(V-E\right)+V^{2} \sinh ^{2}\left(k_{2} L\right)} \tag{6.3}
\end{align}$$ $$\small \begin{align}
T &= \dfrac{|F|^{2}}{|A|^{2}} \\
&=\dfrac{4 k_{1}^{2} k_{2}^{2}}{4 k_{1}^{2} k_{2}^{2}+\left(k_{1}^{2}+k_{2}^{2}\right)^{2} \sinh ^{2}(k_{2} L)} \\
&=\dfrac{4 E\left(V-E\right)}{4 E\left(V-E\right)+V^{2} \sinh ^{2}\left(k_{2}L\right)} \tag{6.4}
\end{align}$$
ここでも関係式 $R+T=1$ が成立していることを確認しよう。$V \to \infty$ とすると $R \to 1$、$T \to 0$ となるが、反射率と透過率は$L$にも大きく影響されることにも注目すべきである。
$E<V$ の場合であっても粒子は壁で完全に遮られることは無く、一部は反射せずに壁の向こう側へ透過する。これは古典物理の知識では全く説明のできない現象である。これを「トンネル効果」という。
本節では有限の高さをもつ矩形ポテンシャルの場合を取り扱った。次節では有限の高さをもつ井戸型ポテンシャルから調和振動子の導入までを扱う。
