４．必要条件で「絞る」

4.1　必要条件の重要性

「必要十分」という言葉は数学のみならず、ビジネスや政治においても使われるポピュラーな言葉ですが、数学をやる上ではその意味をしっかり理解していなければなりません。

数学では「命題と論理」の単元で「必要条件」や「十分条件」という言葉が出てきます。少しおさらいしておきましょう。

命題「$p⟹q$」が真のとき、$p$は$q$であるための十分条件、$q$は$p$であるための必要条件といいます。

また、単に$p$を十分条件、$q$を必要条件と呼ぶことの方が多いです。

今回のテーマは$q$の必要条件の方です。

 

---

$p$を「$n$が$6$の倍数であること」、$q$を「$n$が$3$の倍数であること」とします。このとき、

$n$が$6$の倍数である $⟹$ $n$が$3$の倍数である

は正しい、つまり $p⟹q$ は真です。よって$n$が$6$の倍数であることは、$n$が$3$の倍数であるための「十分条件」となります。

---

理解を助けるために、「集合」の観点から考えてみます。

$3$の倍数の集合を$A$、$6$の倍数の集合を$B$とします。ここで集合$A、B$の包含関係を調べます。感覚的に言えば、どちらの集合の方が「広い」のかを調べます。お馴染みのベン図で考えてみましょう。

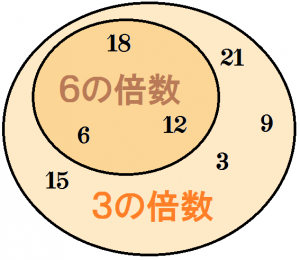
ご覧の通り、３の倍数からなる集合の中に６の倍数からなる集合がスッポリ収まっています。これはつまり、

命題１：$n$が$6$の倍数である $⟹$ $n$が$3$の倍数である

は常に成り立ちますが

命題２：$n$が$3$の倍数である $⟹$ $n$が$6$の倍数である

は常には成り立たないことを表しています。例えば$n=9$としたとき命題２は成り立ちません。

一般に、$p⟹q$ が真のとき、$p$の集合は$q$の集合の中に完全に含まれます。つまり、十分条件を満たす集合というのは必要条件を満たす集合よりも狭いのです。逆に言えば必要条件を満たす集合というのは十分条件を満たす集合よりも広いのです。

整数問題を解決する際には、まず必要条件を満たす解となる数値の「候補」を求めてから、十分性を確認する（＝十分条件を満たすかどうかを確かめること）という方法が非常によく用いられます。つまり、答えの候補の集合の範囲を必要条件によって絞っている、ということです。そうして求めた解の候補が必要十分か否かを確かめて、最終的な答えを得るのです。

簡単な例で見てみましょう。

何となく分かってもらえたでしょうか？十分性を確認せず、$n=1,-2$をそのまま答えにしてしまうと「行ったっきり」の解答になってしまいます。正しい解を求めるには「戻ってこられるのか」をしっかり確認しなければなりません。

---

もう一つ例題で確認しましょう。

$p$を「$n+1$が偶数であること」、$q$を「$n^2+1$が偶数であること」とします。$n+1$が偶数のとき、$n$は奇数であるから整数$m$を用いて$n=2m+1$と置ける。このとき$$n^2+1=(2m+1{)}^2+1=2(2m^2+2m+1)$$となりますから、

$n+1$が偶数である $⟹$ $n^2+1$が偶数である

は正しい、つまり $p⟹q$ は真です。よって$n+1$が偶数であることは、$n^2+1$が偶数であるための「十分条件」となります。

また、$n^2+1$が偶数のとき$n^2$は奇数ですから$n$は奇数となります。このとき$n+1$は偶数となりますから、

$n^2+1$が偶数である $⟹$ $n+1$が偶数である

も正しい、つまり $q⟹p$ も真です。よって$n+1$が偶数であることは、$n^2+1$が偶数であるための「必要条件」でもあります。

したがって$n+1$が偶数であることは、$n^2+1$が偶数であるための「必要十分条件」となります。

 

---

---

前置きはこのくらいにしておきましょう。なぜ整数問題で必要条件が重要かというと、整数の性質と関係があります。それは整数が「数えられる数」であるということです。第２章の第１節冒頭でも触れましたが、整数は範囲を指定しさえすれば人力で数え上げることが可能です。さっきから何度も言っていますが、必要条件であらかじめ解の範囲を広く絞り込んでおいて、残った数個の解の候補が与えられた条件を満たすかどうかを確認する、というのが整数問題の定石なのです。

これを「必要条件で絞る」などと表現します。同値変形する限り、必要十分な解が得られますが、十分性の確認は毎回しっかり行いましょう。次の頁では不等式を利用した必要条件の絞り込みを見ていきます。

 

次へ進む　目次へ戻る