問題#C003 ★★☆☆
$4$(L)のビーカーと$5$(L)のビーカーを何回か使って$49$(L)の水を汲むとき、ビーカーの合計使用回数が最も少なくなるような水の汲み方を答えよ。
《ポイント》
さて、これも現実的に要求されそうな問題ですね。なぜ$49$(L)なのかについては特に理由がある訳ではありませんが・・・。
《解答例》
$4$(L)のビーカーと$5$(L)のビーカーの使用回数をそれぞれ$x$回、$y$回とすると、題意より$$4x+5y=49$$という関係式が成立する。これより$$4(x-1)+5(y-9)=0$$ $$\therefore 4(x-1)=-5(y-9)$$と変形できる。$4$と$5$は互いに素であるから、$x-1$は$5$の倍数、$y-9$は$4$の倍数である。故にある整数$m$、$n$を用いて$$x-1=5m、y-9=4n$$と置くことができて、与式に代入すると$$20m=-20n \ \ \ \therefore m=-n$$となるから、$(1)$を満たすすべての整数解は$$\begin{cases} x=5m+1 \\ z=-4m+9 \end{cases} \ (m \in \mathbb{Z})$$と表される。
$x$、$y$はともに$0$以上でなければならないから、
$\begin{cases} x=5m+1 \geqq 0 \\ y=-4m+9 \geqq 0 \end{cases}$
が必要。故に $m=0、1、2$ に限られ、それらのうち $x+y=m+10$ が最小となるものは $m=0$ のとき、即ち$(x,y)=(1,9)$のときである。
(答)$4$(L)のビーカー$1$回、$5$(L)のビーカー$9$回
《コメント》
「ダイ・ハード3」という映画の中で、「$3$ガロンと$5$ガロンの容器を使って$4$ガロンの水を汲み取るには?」という謎掛け(というか算数?)を解くシーンがあります。これも実は1次不定方程式を解くという操作に当てはめることができ、水を捨てるという操作を負の回数として認めると一応数式化はできます。あとは汲み取る順序を考えるだけですが、実際には水を溜めて置ける場所が2つの容器(と事実上無限の水源)しか無いのでそう単純ではありません。
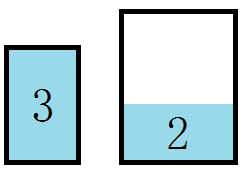
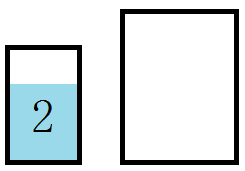
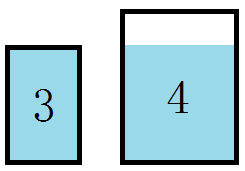
» 答えらしきもの この場合の答えは数パターンが考えられるはずですが、そのうちの一つを紹介しておきます。以下の図では$3$ガロンの容器を小さい方、$5$ガロンの容器を大きい方の枠で表しています。 ①まず$5$ガロンの容器に水を汲みます。 ↓ ②$5$ガロンの容器から目一杯$3$ガロンの容器へ水を移します。 ↓ ③$3$ガロンの容器に移した水を捨て、$5$ガロンの容器に残っていた$2$ガロンの水を$3$ガロンの容器に移します。 ↓ ④$5$ガロンの容器を満タンにしてから、目一杯$3$ガロンの容器へ水を移します。③の時点で$3$ガロンの容器には$2$ガロンの水が入っていたので、$5$ガロンの容器に残る水は$4$ガロンとなり無事解決です。 虚覚えですが実際のシーンでは起爆装置に$4$ガロンの水を入れた容器を乗せることで起爆を解除していたはずです。意外と簡単に解けてしまいますが、パニックの中でこれを行うのは容易ではないでしょうね。 » 閉じる