問題7.1.7
曲線$C$は$(1,1)$を通り、$C$上の任意の点$\mathrm{P}$における接線と$x$軸との交点を$\mathrm{Q}$とすると、線分$\mathrm{PQ}$は$y$軸によって2等分される。曲線$C$の方程式を求めよ。
《ポイント》
問題文の条件から微分方程式を立式します。最終的には変数分離型の微分方程式に帰着します。
《解答例》
点 $(x_1,y_1)$ における $C$ の接線は$$y-y_1=y'(x-x_1)$$となるから点$\mathrm{Q}$の $x$ 座標は $$x=-\dfrac{y_1}{y’}+x_1$$となる。線分$\mathrm{PQ}$は $y$ 軸によって二等分されるから、$\mathrm{PQ}$の中点の $x$ 座標は $0$ である。よって$$\left(-\frac{y_{1}}{y^{\prime}}+x_{1}\right)+x_{1}=0$$ $$\therefore y^{\prime}=\frac{y_{1}}{2 x_{1}}$$を得る(ただし $x_1 \ne 0$ )。これは $C$ 上の任意の点で成り立つから、微分方程式 $$y^{\prime}=\frac{y}{2 x} \quad (x \ne 0)$$が成立する。
よって$$\begin{aligned}
\int \frac{1}{y} d y&=\frac{1}{2} \int \frac{1}{x} d x \\
\therefore 2\log |y|&=\log |x|+c_{1} \\
\therefore \log y^{2}&=\log |e^{c_{1}}x| \\
\therefore y^{2}&=e^{c_{1}}|x|
\end{aligned}$$となる。曲線$C$は$(1,1)$を通るから、代入して $c_{1}=0$ を得るので、求める曲線は$$y^2=|x| \quad (x \ne 0) \quad \cdots (\text{答})$$である。
【※注意】教科書に掲載されている本問の解答は十分性しか満たしておらず厳密には正しくありません。$y^2=|x| \quad (x \ne 0)$ のグラフは以下の通りです。この曲線は原点で不連続ですが本問の条件を満たしています。後から原点を付け加えることもできますが「線分$\mathrm{PQ}$は$y$軸によって2等分される」という条件を考えると原点を除外しておくのが適当だと思われます。
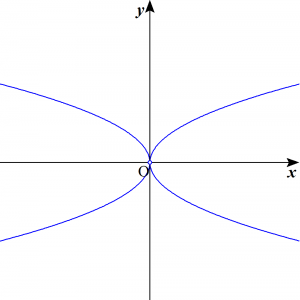
もし、問題文中の「曲線」という語が「連続な曲線」を指しているのであれば、$y=\sqrt{x}$ だけでも答として認められるでしょうが、複数の答えが想定される時点で問題の不備と言えます。
復習例題は設定していません。
