問題3.1.4
$S_4$の元を全て求め、偶置換と奇置換に分けよ。
(1)$\left(\begin{array}{cccc}1 & 3 & 6 & 4\end{array}\right)$
(2)$\left(\begin{array}{ccccc}1 & 2 & 5 & 3 & 4\end{array}\right)$
(3)$\left(\begin{array}{ccc} 2 & 4 & 6\end{array}\right)$
(4)$\left(\begin{array}{lllllll}
1 & 2 & 3 & 4 & 5 & 6 & 7 \\
3 & 7 & 4 & 1 & 2 & 5 & 6
\end{array}\right)$
(5)$\left(\begin{array}{lllllllll}1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ 3 & 4 & 1 & 9 & 8 & 6 & 5 & 7 & 2\end{array}\right)$
ポイント
教科書に従うと、$n$文字の置換全体を$S_n$とします。$$\sigma=\left(\begin{array}{cccc}
1 & 2 & \cdots & n \\
k_{1} & k_{2} & \cdots & k_{n}
\end{array}\right)$$は $k_{1}$、$_{2}$、$\cdots$、$k_{n}$が定まれば一意に決まるから、$S_n$の元の個数は個の順列の個数に等しく、$n!$個存在します。
今回は $n=4$ なので合計$24$個の置換を数え上げる必要があります。順列は樹形図などを使えば効率的に数え上げることができます。例えば以下のように数え上げる場合、数字の色とマスの色が異なる個数が偶数なら偶置換、奇数なら奇置換となります。
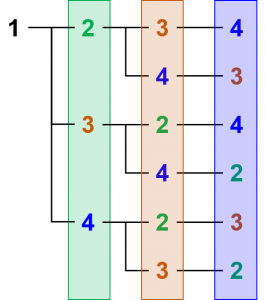
解答例
(省略)
※ 解答は教科書を参照のこと。
