線形代数3.2.1

トップへ戻る　次の問題へ

 

 問題3.2.1

次の２次、３次の行列式をサラスの方法を用いて求めよ。

（１）|1324|

（２）|abcd|

（３）|123052716|

（４）|3−2−52346−16|

 

 ポイント

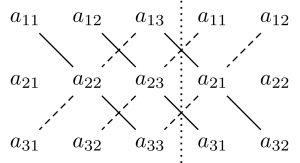
サラスの方法は２次、３次の行列式を求める際に有効です。３次の場合は以下のように積を取ります。符号は実線が+、破線が−です。

 

 解答例

（１）

|1324|=1⋅4−3⋅2=−2⋯(答)

（２）

|abcd|=ad−bc⋯(答)

（３）

|123052716|=1⋅5⋅6+2⋅2⋅7+3⋅0⋅1−3⋅5⋅7−2⋅0⋅6−1⋅2⋅1=−49⋯(答)

（４）

|3−2−52346−16|=3⋅3⋅6+(−2)⋅4⋅6+(−5)⋅2⋅(−1)−(−5)⋅3⋅6−(−2)⋅2⋅6−3⋅4⋅(−1)=142⋯(答)

 

トップへ戻る　次の問題へ