微分積分学の歴史
微分積分を指す「ビセキ」という言葉は、高校生以上の年齢の方には随分と馴染み深い言葉でしょう。この「ビセキ」の概念を高校生が学べるようになるまでに費やされた先人の苦労を忍び、それが如何にスゴイことなのかを理解するため、微分積分学の歴史的経緯について簡単に振り返ってみましょう。
● ● ● ● ●
古代ギリシャでは既に現在の積分に似た方法が考えられていました。これは「取り尽くし法」と呼ばれています。「取り尽くし法」とは、ある図形に内接する多角形を考えることで、その図形の面積や体積を求める方法のことです。この方法はギリシャの哲学者アンティポンにより考え出され、ギリシャの数学者エウドクソスにより論理性を保証されました。アルキメデスやユークリッドはこの取り尽くし法を用いて種々の図形の求積を行っていますし、アルキメデスはこれ利用した級数の評価にも成功しています。
これらは紀元前3~5世紀の話で、今から2000年以上も昔のことなのです。放物線と直線の囲む図形の面積なんかもこの取り尽くし法で求めることができます(以下の図.1参照)。
時代は下り、16世紀。カヴァリエリの原理で知られるイタリアの数学者カヴァリエリや、数学に文字記号を導入したフランスの数学者ビエトなどが、これらの解析的手法を再び西欧の数学界に持ち込み、デカルト、パスカル、フェルマー、ウォリスなどの手により研究が発展していきました。
● ● ● ● ●
・・・ところで、紀元前3世紀から16世紀までのおよそ2000年間、ヨーロッパの数学者達は何をしていたのでしょう?こんなに時間があるならもっと数学の研究が進んでいてもおかしくありません。
もちろん数学という学問は存続していましたし研究自体も(細々と)行われていましたが、当時のイスラム圏やインドの数学からは遅れていました。これには幾つかの理由が考えられます。
まず第一に、当時のヨーロッパは「暗黒時代」と呼ばれる文化の停滞期に入っていたため、数学のみならず、あらゆる学問や芸術が衰退していました。年表付きの絵画集などを見てもらえれば、聖母マリアを描いた絵の質がルネッサンス期に入る前と後で激変しているのがお分かりになると思います。古代ギリシアの文化を復興しようとする試みが「ルネッサンス」(文芸復興)ですから、大昔の文化を復活させなければならないまでに当時の文化は荒れ果てていました。この暗黒時代は、戦乱、疫病、宗教的抗争など様々な原因が重なったことや、それにより文化や技術を継承できなかったことなどのために何と1000年以上にわたって続いてしまいました。この苦難の時代の後に、数学をはじめ、様々な学問の研究が爆発的に発展していきます。
第二の理由は、表記法が非常に不便であったことです。当時の数学にはまだ$x$や$a$などの文字で考える習慣が無く、アラビア数字ではなくローマ数字を使用していた上に、等号や四則演算の記号すら発明されていませんでした。そのため、簡単な数学の議論であっても膨大な文章を書かねばならず、研究が進みにくかったと考えられます。これを解決したのが先ほど紹介したフランスの数学者ビエトでした。現代では当たり前のように使われている記号が16世紀まで存在していなかったというのだから驚きです。
そして第三の理由は、印刷技術が存在しなかったことです。15世紀にドイツのグーテンベルクが活版印刷技術を発明するまでは、論文のように長大な文章を複製して広く公表したり出版することなどが難しく、また当時は郵便制度なども発達していなかったため、数学者間の交流はごく小さいものでした。印刷技術や郵便が整備されてくる16世紀になると数学者間の交流が活発に行われるようになりました(パスカルとフェルマーの文通の中で確率論が興ったのは有名な話ですね)。
・・・などなど色々な理由により、西洋数学の発展は16世紀頃まで待たねばならなかったのです。
● ● ● ● ●
さて、17世紀になると微分積分学における超重要人物が2人も登場します。その2人の人物とは、イギリスの自然哲学者であったニュートンと、ドイツの哲学者であり数学者でもあったライプニッツです。この2人は数学に多大な貢献をした人物として知られています。その最たる業績がこの微分積分学の創始でしょう。
超重要人物が2人、と言いましたが、実は、彼らは2人で仲良く微分積分学を作った訳ではありません。寧ろ2人はどっちが先に微分積分学を創始したかについてイギリスとドイツの学会を交えて(かなり)激しく争った仲でした。年代的に言えば、微分積分の概念を発想したのはニュートンが先でしたが、論文として公表し世に送り出したのはライプニッツの方が先でした。そのためイギリスの学会は、ライプニッツはニュートンの未発表論文を剽窃したと非難しました。当然ライプニッツ側も黙っておらずニュートンこそ剽窃したに違いないと非難し、激しい非難の応酬が何年もの間にわたって続くことになってしまうのですが、彼らの微分積分学の組み立て方はやや異なっており、現在では2人は独立に微分積分学を構築したと考えられています。
ニュートンとライプニッツが登場するまで、微分的手法と積分的手法は全く関係の無い別物の演算と考えられていました。彼らの発見の凄い点は、微分と積分が逆の関係にある演算であることを見抜いた所です(ただし完全な逆演算ではありません)。これは微分積分学の基本定理によって保障されている事実であり、「微分が先か、積分が先か」という議論は「卵が先か、鶏が先か」という議論に似ています。微分積分学の基本定理によると、$$F(x)+C=\int f(t) dt$$が成立します。これは「(狭義の)リーマン積分」というのですが、簡単い言えば微小区間に分割した領域の足し合わせという意味付けが為されています。
ニュートンはこの方法を「流率法」と呼び、自然科学の諸分野に応用して多くの成果を得ました。物理法則を数学的に記述する方法として流率法は非常に有用でした。ニュートンの歴史的著作である「プリンキピア」には手法そのものこそ現れませんが、考え方などは流率法を用いている箇所もあるそうです。
ライプニッツは微分積分学を学ぶ者に対して非常に大きな貢献をしました。というのも、現在使われている$\dfrac{d}{dx}$や$\displaystyle \int$などの記号は、実はライプニッツが考案したものなのです。彼は数式の記述方法に特に気を遣っていたようで、どういう記号を用いれば演算を簡潔に表現できるかについて、何日もかけて悩んだと言われています。その甲斐あってか、イギリスではそれほど微分積分学の研究が進まなかったのに対して、大陸側では微分積分学が盛んに研究されました(先程述べた通り、イギリスとドイツでは微分積分学の創始者について激しくいがみ合っていたので、イギリスでライプニッツの考案した記法が使われるはずもありませんでした・・・)。
余談ですが、日本でも和算が世界的に見ても驚異的な発展を遂げ、微分積分学に匹敵するか、という所まで行ったのですが、表記法などが不完全・不便であったため、微分積分を発明するまでには至りませんでした。このことからも、数学の発展にとって数式の表記法が如何に重要な要素であるかが窺えます。解析学の発展に寄与したライプニッツの偉大さがお分かり頂けると思います。
● ● ● ● ●
その後、近代数学の発展に伴って、オイラー、ガウス、ディリクレ、コーシー、リーマン、ワイエルシュトラスなどの近代を代表する大数学者の活躍により、微分積分学は厳密に定義され整備されていきました。現在では「解析学」として数学の三大分野の一角を成す大きな学問領域に発展し、今なお多くの研究者が研究に明け暮れています。
解析学は数学という一つの分野だけでなく、物理学や天文学、化学など、自然科学のあらゆる分野で役立っています。特に理系の(本来は文理問わないのですが)学生の皆さんは将来、解析学の様々な手法を利用することになると思います。科学技術の発展はまさに微積分学の発展とともにあると言うべきでしょう。
まだ16、7歳くらいの特に数学に興味も持たない若者達が、かくも簡単に微分積分学を学べる時代になったということは、これまでに見てきた微分積分学の歴史を考えれば驚嘆すべきことだとは思いませんか?思いますよね?是非思ってください(笑)。そしてこの学問の重みを噛み締め、先人達の苦労に感謝しながら勉強に努めてほしいと思います!

 アルキメデス(希:B.C.287(?)~B.C.212)
アルキメデス(希:B.C.287(?)~B.C.212)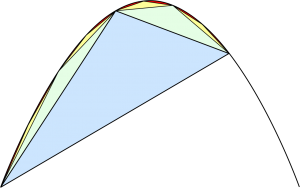

 デカルト(仏:1596~1650)
デカルト(仏:1596~1650) ニュートン
ニュートン

