数列に関する備忘録
等差数列の一般項と総和の求め方
「等差数列」(またの名を「算術数列」)とは、「隣接する項が共通の差(公差)を持つ数列」を指します。
例えば、
$1$、$4$、$7$、$10$、$\cdots$
という数列は「初項が$1$で、公差が$3$の等差数列」となります。公比数列と並んで学力テスト(旧センター試験)で頻出の数列です。
「初項が$p$で、公差が$d$の等差数列$a_n$」の一般項は$$a_n=p+(n-1)d\ \ \ (n=1,2,3,\cdots)$$と表せます。$a_1$に $n-1$ 個の$d$を足せば$a_n$になるので納得ですね。
※ $a_n=p+nd$ とするのは誤りです。例えばこれに $n=1$ を代入すると $a_1=p+d$ となって $a_1=p$ に矛盾しますよね?
また、「初項が$p$で、公差が$d$の等差数列$a_n$」の第$1$項から第$n$項までの総和は$$\begin{align}S_{n} &= \sum _{k=1}^{n}a_{k} \\ &=a_{1}+a_{2}+\dots +a_{n} \\ &=\dfrac {n(a_{1}+a_{n})}{2} \\ &=\dfrac{n\{2a_{1}+(n-1)d\}}{2}\end{align}$$となります。これは以下のように簡単に導出することができます。例として「初項が$1$で、公差が$3$の等差数列$a_n$」の総和を求めてみます。
総和の図形的なイメージは次のようになります。
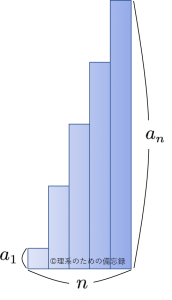
これを以下のように2つ足し合わせます。
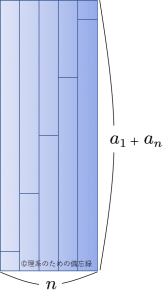
この長方形の面積は $n(a_{1}+a_{n})$ となるので、元の総和はこれを$2$で割って$$S_{n}=\dfrac{1}{2}n(a_{1}+a_{n})$$を得ます。
教育関係者の方々にはただ単に公式を暗記させるのではなく、このように視覚に訴える方法で学生の記憶に残してあげるようにして欲しいと思います。
