【物理の心】
「質点」という考え方
物理のモデルでは物体を「質点」として扱うことがあります。この質点という考え方によって物体の運動が単純化され、数学的に（解析的に）取り扱いやすくなります。本稿では「質点」とはどういった概念なのかを解説します。
力学＝物体の運動を解析する学問
皆さんもご存知の通り、物理学には物体の運動を幅広い観点から調べる「力学」という一大分野が存在します。この力学という学問は幾つかの系統に分けることができて、高校物理では「古典力学」、特に「ニュートン力学」と呼ばれる種類の力学を学びます。
「古典力学」はアイザック・ニュートン（英：1642年～1727年）によって切り拓かれた近代自然科学の草分け的な学問分野であり、後の時代の近代物理学の基礎とも言える存在です。そんなわけで、高校に入学した学生は物理学として最初に力学を習います。近代科学の成り立ちの歴史を考えれば「物理と言えば力学」という見方にも納得できますよね。
力学は物体の運動を調べる学問ですが、その際に障害となる問題があります。それは、
「物体には『大きさ』がある」
ということです。全く当たり前のことなのですが、このことにより物体の運動を把握するのが難しくなっているのは事実です。
そこで、ニュートンは大胆にも「物体の大きさを無視する」という近似を取り入れて、物体をある種の「点」と見なして物体の運動を調べることを思いつきました。これが「質点」という考え方の始まりです。
現実の物体は変形する
ところで世の中を見渡すと、物体の大きさをどうしても無視できない運動も存在します。
例えば、自動車の衝突実験では衝突後の自動車は大きくひしゃげてしまうでしょうし、ビーカーに入っている水はフラスコにもシリンダーにも移し替えることができますし、筋トレによく使われるゴムチューブは引っ張れば伸びるし手を離せば元の大きさに戻ります。
このように物体には一定の形状を維持しないものも多くあります。そこで、力学では取り扱う物体を大きく４種類に分けて考えることにしています。
-
- 質点 ･･･ 質量はあるが大きさを持たない仮想的な点
- 剛体 ･･･ 決して変形することのない、大きさのある物体
- 弾性体 ･･･ 力を加えると変形するが、力を除くと形が元に戻る物体
- 流体 ･･･ 容器によって自由に形を変えられる物体
この説明を見ても分かる通り、質点が最も単純で取り扱いが簡単そうに思えますよね。という訳で、高校物理で学ぶ力学では、これらのうち「質点」と「剛体」を主に扱います。「弾性体」もバネやゴム紐などとして登場することがありますが、「大きさ」や「質量」を持った弾性体は高校物理では扱いません。
これから高校で物理を学ぶ方（もちろん、これから物理を学び直そうとしている方も）は、まず質点の運動を解析するところから始めればよい、ということになります。
こういった事情により、「質点」という「質量というものを持っている何だかよく分からん点」の運動が物理の教科書の最初の方に書いてあるのです。
質点＝質量をもった点
高校物理の課程では、いきなり運動の法則が出てきたり、運動方程式が云々…と始まりますが、その前に「質点」という概念をよく理解しておくことは重要です。
「質点」とは、ずばり「質量をもった点」のことを指します。ニュートン力学の画期的なところは「質量」という量を導入して「動力学」の解析手法を確立したところにあります。
※それ以前の物理学では静止した物体を扱う「静力学」が発達しており、古代ギリシャ時代から研究が積み重ねられていました。「動力学」はニュートンが体系化しましたが、全て彼一人の力で一つの学問を創り上げた訳ではありません。ガリレオの落体の法則や慣性の発見、ケプラーの惑星の運動に関する法則など先人たちが遺した成果を基礎として構築されており、「自然哲学の数学的諸原理」、通称「プリンキピア」という全3巻の大著として体系的にまとめ上げられています。
「質量」とは、物体のがどのくらい動かしにくいのか（＝「慣性」の大きさ）を数値化した量です。古典力学の範囲では質量は物体に固有の値を取ります。物体が分裂したり接着したりする場合を除き、勝手に増減する事はありません。
※「質量は物体に固有」というのは現実世界でも同じです。1円玉の重さが昨日は1gだったのに今日は10gに増えている、なんてことは起こりませんよね。
この「質点」という近似を導入することで現実世界を理想化＆抽象化することができます。何だか難しそうに聞こえるかもしれませんが、要するに「現実世界は複雑すぎるから思い切って単純に考えてしまおう！」という発想です。
力学ではよく、様々な物体を理想化＆抽象化して捉えるために物体を質点と見なして考えることがあります。これは別の言い方をすれば、
「質量」という値をもつ「数学的な点」
を導入したとも言い換えられます。
この「数学的な」というところがポイントです。例えば太陽と地球はそれぞれ物凄く大きな物体ですが、これらを質点と見なして単純なモデルに置き換えてしまうことができます。一見すると大雑把に思われるかもしれませんが、このような単純なモデルでも２つの天体の運動はそれなりの精度で解析できますし、むしろその方が数学的には扱いやすくなります。
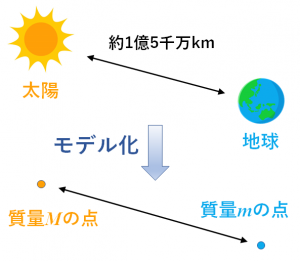図．モデル化の例
力学の基本的な考え方は、物体の運動を数学的に捉える、ということです。物体の運動が何らかの規則（方程式や数式）に従っていれば、その規則に基づいて物体の運動が予測できます。つまるところ、力学の目標は「あらゆる物体の運動を予測･予言する」ことにあり、これは物理学が究極とする到達点でもあります。
物体の運動は数学的である、いや、数学的でなければならない、というのが物理学･力学の精神なのです。ガリレオ･ガリレイ（伊：1564年～1642年）が落体の法則や慣性を発見した16世紀後半以降、物理学は一定時間後の未来の状態を予言することができる学問として発展してきました。一般性のある法則に基づいて物体の運動を予言できれば、その法則には普遍的な価値があります。そうした法則は大抵の場合、数学によって表現することができます。そのため、数学的な道具によって物体の運動を解析することはとても自然な発想なのです。