運動の基本原理は「運動の3法則」です。力学の土台となる重要な法則なのでしっかり覚えましょう！ また、物理学で重要な「系」という考え方についても復習しておきます。
「運動の3法則」とは
「運動の3法則」とは、ニュートンによってまとめられた運動の基本原理です。この法則を認めた上で理論が構築された力学体系を「ニュートン力学」と呼びます。
日本の高校物理で学ばれる力学はニュートン力学には違いなのですが、全くと言って良いほど微分積分の知識を使わず、むしろ避けまくって授業が進められるため、話の流れが掴みにくいカリキュラムになってしまっています。残念なことです。
･･･それはそれとして、「運動の3法則」は1687年に刊行されたニュートンによる大著「自然哲学の数学的諸原理」通称「プリンキピア」(Principia) を通して公表されました。それぞれの法則を列挙しておきます。
運動の第１法則：
すべての物体は、外部から力を加えられない限り、静止している物体は静止状態を続け、運動している物体は等速直線運動を続ける。「慣性の法則」とも呼ばれる。
運動の第２法則：
質点の加速度$\vec {a}$は、そのとき質点に作用する力$\vec {F}$に比例し、質点の質量$m$に反比例する。この法則によって与えられる方程式は「運動方程式」と呼ばれる。
運動の第３法則：
２物体が互いに力を及ぼし合うとき、それらの力は向きが反対で大きさが等しい。「作用・反作用の法則」とも呼ばれる。
いずれも運動という物理的な現象の基礎となる重要な法則です。以下、具体的にどんな法則なのかについて、それぞれ紹介していきます。
運動の第１法則
運動の第１法則は別名「慣性の法則」と呼ばれるもので、物体は力を及ぼされない限りそれまでの運動を続けるというものです。
例えば、時速 80 km で走行する列車の中でジャンプしても（床から離れたのに）後ろに置いていかれたりすることありませんよね。これは、列車の中では人間も列車と同じ速度で移動しているためです。列車の中では地上と同じようにキャッチボールをしたりすることもできますが、これは人間もボールも（車内の空気も）列車に対する相対速度がゼロである（同じ速度で運動している）ためです。このように、等速直線運動している物体は、力を及ぼされない限り等速直線運動を続けます。
等速運動だけが運動に含まれるわけではありません。「静止」も歴とした運動の一種です。例えば、だるま落としは慣性を利用した遊びです。真ん中のブロックを勢いよく抜き去っても、上に乗っている積み木は静止を続けます。それゆえ、上のブロックがそのまま落ちてくるのです。このように、静止している物体は、力を及ぼされない限り静止し続けます。
このように、日常生活の身近なところに慣性が存在しているということがお分かり頂けると思います。
図．だるま落としのイメージ
運動の第２法則
運動の第２法則によって導かれるのが「運動方程式」です。運動方程式は前回ちょっとだけ紹介しましたね。質点の加速度の大きさを$a$、作用する力の大きさを$F$、質点の質量を$m$とすると、これらの物理量は次の等式を満たします。$$F=ma \tag{1}$$これはベクトルについて成り立つ式なので、正確には$$\vec{F}=m\vec{a} \tag{2}$$という形で書き表されます。
この式が意味するのは次の２点です。
① 加速度の向きは作用する力の向きに一致する
（$\vec{a}$は$\vec{F}$の定数倍になる）
② 加速度の大きさは $|\vec{a}|=\dfrac{|\vec{F}|}{m}$ で与えられる
（$|\vec{a}|$は加速度の大きさ、$|\vec{F}|$は力の大きさ）
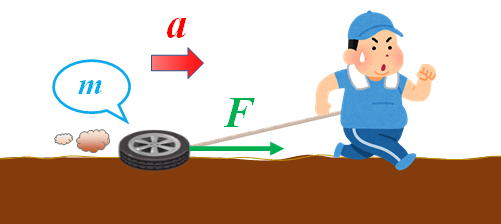図．力を及ぼすと加速度が発生する
運動の第２法則に基づいて与えられる運動方程式は力学の根幹・土台とも言える等式であり、この式が力学の出発点とも言えます。なぜなら、運動方程式から加速度が分かれば一定時間後の速度や位置が割り出せるからです。これにより、数学的な操作を用いて物体の運動を解析・予測することができるようになるため、運動方程式は物理学の予言性を確立するとても重要な手段なのです。
微分積分を用いた運動方程式の具体的な運用方法については各論で述べますので、楽しみにしていて下さい！
運動の第３法則
運動の第３法則はいわゆる「作用･反作用の法則」と呼ばれるもので、単独で物体に働く力というものは存在せず、必ず逆向きで大きさが等しい力が存在している、と主張する法則です。
例えば、手押し相撲をして遊んでいるときを想像してみて下さい。相手の手を押した時、自分の手も相手によって全く同じ大きさの力で逆向きに押されているのです。同じことはスケートリンクの上での押し合いや、水上のボートの上での押し合いなどでも言えます。相手を押せば自分も後ろに初速が付きますが、これこそ作用･反作用の法則によるものなのです。
作用･反作用の法則を体現する有名な玩具に「ニュートンのゆりかご」があります。これはそれぞれの鉄球が互いに押し合って力が伝わることで端の鉄球が振り子運動するというものです。それぞれの鉄球には作用･反作用の法則により、互いに逆向きで大きさの等しい力が瞬間的に働きます。もし一方向にのみ力が働いているのであれば、すべての鉄球が同じ方向に一斉に動き出すはずですよね？ 真ん中の鉄球が見かけ上静止しているということは、作用$\vec{F}$に対して逆向きの反作用$-\vec{F}$が働いているという証拠に他なりません。
図．ニュートンのゆりかご
この運動の第３法則は、物体に働く力を作図する上でも非常に重要なポイントとなります。力の作用点を始点として力$\vec{F}$を加えると、同じ作用点を始点とする全く同じ大きさの逆向きの力$-\vec{F}$が働きます。これが反作用の力です。
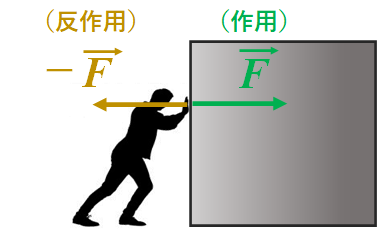図．物体を押す人は物体から押し返される
このような物体に働く力の作図では、作用･反作用の法則を意識して力のベクトルを図示することが大切です。今は何となく、そういうものなのかと理解しておいて下さい。
作用･反作用はどこまで考えれば良い？
ところで、私たちが普段生活する中で、物体をある程度の大きさの力で押すと、その物体は動き出しますよね。つまり私たちは物体に作用を加えることで物体を動かしています。ということは作用･反作用の法則により、私たちは全く同じ大きさの力で物体から押し返されているはずです。でも反作用があるのに、私たちが押し返されて後ろの方にひっくり返る、なんてことはありません。
それは私たちが地面や床から摩擦力を受けているからです。この力$\vec{f}$が反作用$-\vec{F}$と打ち消し合うため、人が動くことはありません。もし摩擦力が無ければ、物体を押すために踏ん張ることができませんよね。
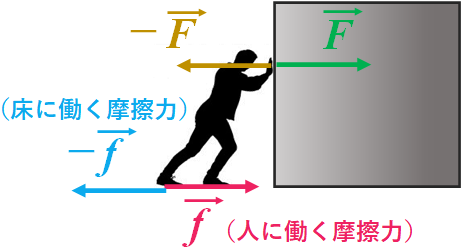
図．床と人には摩擦力も働く
しかし、床に働く摩擦力はどこにいくのでしょうか？ 床には確かに作用･反作用の法則により、人に働く摩擦力と同じ大きさで逆向きの力が加わっているはずです。そこで今度は床の方が動いてしまわないか不安になってきます。
さらには、もし仮に床の摩擦力の謎が解決できても、この人の立っている床と建物との摩擦や、その建物と地面との摩擦も考えていくと、無限に作用･反作用の法則が適用できてしまいそうな気がします。
「系」という考え方
実は、無限に作用･反作用を考えること自体は可能です。しかし、その考察には物理的な意味がありません。いちいち地球の運動まで考慮に入れていてはキリがないからです。そこで、物理的な考察の対象とする物体の範囲を制限して様々な現象を考えるのが一番良さそうです。例えば上の図で言うと、せいぜい床まで考えれば物体の運動を十分に捉えることができますよね。
このように、物理的な考察の対象として制限された物体の範囲･集合体を「系」と呼んでいます。物理の問題ではそのような「系」を考えることにより、現象を単純化して考察します。
分かりやすい例を考えてみましょう。下の図は、上空のカラスがクルミを自由落下させている様子を描いたものです。
図．クルミの自由落下
このとき、クルミには重力が働いています。この作用の主体は地球ですから、当然地球は反作用の力を受けているはずです。しかし地球はあまりにも大きく重いので、クルミが落下したところで地球の運動が変わることはありません（もし変化していたとしても全く気付かないほど微小です）。つまり、クルミの自由落下を考察する際はクルミと地面だけを「系」として考えれば十分正確に運動を記述できることが分かります。この理由により、重力の反作用は無視しても困らないのです。
このように作用･反作用の法則は常に成り立ちますが、その実体を延々と考えるようなことはしません。運動を考える際は「系」という物体の周辺のみに注目して考察すれば良いのです。
そこで、系の内部だけで力のやり取り(相互作用)が完結している場合、そこで働く力を「内力」(ないりょく) と呼び、系の外部の何らかの物体とも力のやり取りがある場合、そこで働く力を「外力」(がいりょく) と呼びます。
自由落下のときに働く重力は、クルミと地面を系とした場合は「外力」として扱われます。摩擦力のように反作用の相手を曖昧に考えるものは外力です。これに対して水上のボートの上での押し合いでは２つのボートを系と見なすと内力しか働きません。バネで繋がれた小球なんかも内力しか働いていません。
図．バネで繋がれた小球
今後「エネルギー」という新しい物理量を学ぶ際に、この「内力」と「外力」の区別が重要な意味を持ちます。
※「重力の反作用は地球の中心に現れるから図には出てこない」という説明で済ませている参考書も多いですが、力が図からはみ出していることは重力の反作用を無視できることの根拠にはなりません（結局は無視しても構わないのですが）。全く個人的な意見ですが、この「系」という考え方ついてきちんと教えてくれる物理の先生は良い先生だと思います。