このページでは「力の合成」と「力の釣り合い」という力学における大切な要素を扱います。力の釣り合いという現象が運動方程式によって自然に表せることを学びます。
力はベクトルである
これまで見てきたように、物体に働く力は「大きさ」と「向き」という２つの量を持つベクトルで表現できます。力を図示するときは矢印（「有向線分」と呼ばれる向きを持った線分のこと）で力を表します。ベクトルを学んだことのある方にとっては常識だと思いますが、ベクトルは合成したり分解したりすることができます。
例えば平面上の$\vec{a}$と$\vec{b}$という２つのベクトルは $\vec{a}+\vec{b}$ として下図のように合成することができます。
図．ベクトルの合成の例
この例ではベクトルを２本しか考えていませんが、見方を変えて逆に考えると、１本のベクトルを２本以上のベクトルに分解できるということも分かります。例えばベクトル$\vec{F}$は平面上の$\vec{f_1}$と$\vec{f_2}$という２つのベクトルに分解することができます。
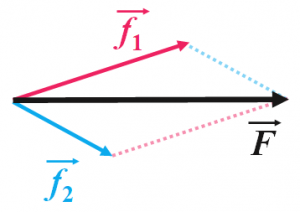図．見方を変えればベクトルの分解
力はベクトルなので任意に合成･分解が可能です。特に２つ以上の力を合成して得られる新たな力を「合力」(ごうりょく) と言います。
力の他にも速度や加速度もベクトル量なので複数方向に分解して考えることができます。これにより、例えば$x$方向と$y$方向の運動を切り分けて考察することが可能になります。これは放物運動や斜面上の運動を考える場合に有効です。このような問題の具体的な解き方については各論で解説します。
力の釣り合い＝合力がゼロ
運動の第２法則より、力を及ぼされた物体には加速度が生じます。加速度が生じると多くの場合、運動が変化します。しかし、ある条件が成り立つときは力を加えているにもかかわらず物体の運動が変化しないことがあります。
例として、綱引きをしている場面を想像してみて下さい。
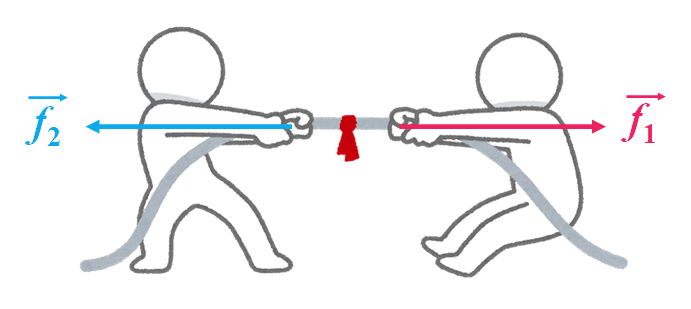図．綱引きのイメージ
互いに一進一退の攻防を繰り広げる接戦だとしましょう。ときに両者の実力は拮抗して膠着状態となり、外から見ると静止しているように見える時間があります。
このとき、両者が綱を引く力の大きさは一致しています。つまり、合力 $\vec{f_1}+\vec{f_2}$ はゼロベクトルになっています。これを式にすると$$\vec{f_1}+\vec{f_2}=\vec{0} \tag{1}$$と表せます。$\vec{f_1}$と$\vec{f_2}$という２つのベクトルの向きは互いに逆方向なので、大きさが等しければ足し合わせるとゼロになるというのは自然ですよね。
力の釣り合いと運動方程式
ここで、この２人に引っ張られている綱に着目してみます。
綱の重さを$m$、加速度を$\vec{a}$とすると、運動の第２法則により得られる運動方程式は$$\vec{f_1}+\vec{f_2}=m\vec{a} \tag{2}$$となります。ここで両者が拮抗して静止している状況では、加速度はゼロです。つまり $\vec{a}=\vec{0}$ となります。これを$(2)$式に代入してみると、運動方程式は$$\vec{f_1}+\vec{f_2}=m \cdot \vec{0} \tag{3}$$となります。
つまり「力の釣り合い」という現象は運動方程式（運動の第２法則）から自然に導かれるものなのです。「加速度がゼロ」という状態こそが力の釣り合っている状態に相当するのです。
世の中には力の釣り合いを運動方程式と切り離して考えるよう指導されることもあるようです。しかし、これは力学の精神に照らしてナンセンスであり、静止も含めた「運動」という現象が運動方程式によって一般的に記述されるというニュートンの運動の法則を蔑ろにする姿勢だと言えます。もちろん「加速度がゼロ」という特殊な場合についてわざわざ運動方程式を立てて考える必要なんて無いじゃないか、という考えも理解できます。しかし、学生に力の釣り合いを始めて教える際は、運動方程式との関係に必ず言及して頂きたいと思います。運動を解析する上で最も基礎的な道具が運動方程式であるという認識はこれから力学の学習を進めていく上でとても大切だからです。