運動する物体は「質点」としてモデル化することができます。質点の運動を調べるには、まずその位置を決める必要があります。本稿では質点が置かれる「座標系」について解説します。
「直交座標系」
座標という考え方は、フランスの哲学者であり数学者でもあるルネ･デカルト（仏：1596～1650年）が初めて提案したと言われています。
ルネ･デカルトの肖像画
※デカルトは「我思う、故に我あり」という哲学史上で最も有名な命題の提唱者として知られ、「近代哲学の父」と称される人物です。
最も単純な座標系は１次元の座標（数直線）です。座標系を組み立てるにはまず基準となる点を決め、そこから座標軸を取ります。この基準点$\mathrm{O}$を「原点」と呼び、原点を通る座標軸上の値「$x$」を質点の「$x$座標」と言います。
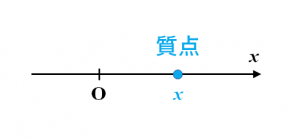図．１次元の座標系（数直線）
最もよく知られている（使われている）座標系は「直交座標系」と呼ばれるものです。これは座標軸が互いに直交していることからそのように呼ばれています。例えば、皆さんも良く知っている「$xy$座標」は直交座標系の一つです。
直交座標系には２次元、３次元の座標系が考えられ、運動が平面上に限られる場合は２次元の直交座標系が用いられます。このような運動を平面運動と呼んだりします。質点の位置は$x$方向にいくら$y$方向にいくら、というように２つの実数の組 $(x,\,y)$ として表現されます。
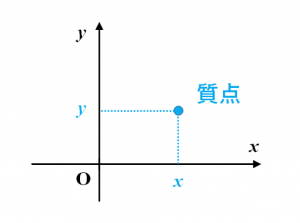図．２次元の座標系（平面座標）
さらに３次元方向の運動も考慮する場合は、空間内に基準点を定め、直交する３本の座標軸を引き、３次元の直交座標系を定めます。$xy$座標に「奥行き(高さ)」という新しい軸が加わった$xyz$空間座標がこれに当たります。
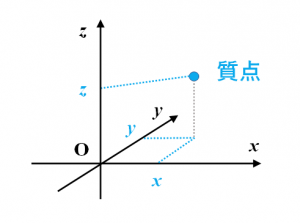図．３次元の座標系（空間座標）
直交座標系は発明者のデカルトに因んで「デカルト座標系」もしくは「カーテシアン」(Cartesian coordinate system) と呼ばれることもあります。
※この「カーテシアン」という名称は「レナトゥス・カルテシウス」(Renatus Cartesius) というデカルトのラテン語名に由来しています。大学の物理の講義ではカーテシアンという名前がいきなり登場することがあるので、初めて聞く人は何の事だか分からないかもしれませんね…。
「極座標系」
直交座標以外にも座標系が存在します。
一定の円軌道を周回するような運動を記述する場合は、直交座標を用いるよりも「極座標」を用いた方が便利です。
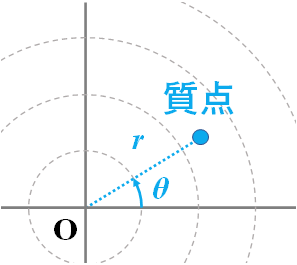図．２次元の極座標系
基準点を「極 (pole)」、原点→質点までの符号付き長さを「動径 (radius)」と言います（動径は負の値もとります）。角度$\theta$は英語では “angular coordinate” と呼ばれます。複素数平面における極形式になぞらえて「偏角 (argument)」と言うこともありますが、極座標においてはそれほど一般的な呼び方ではありません。
極座標では$r$と$\theta$の２つの変数で位置を記述します。円運動などでは$xy$座標系で位置を表現するよりも極座標を用いた方がシンプルになることが多いです。なお、極座標についても三次元極座標が考えることできますが、少し難しいのでここでは詳しく紹介しません。
座標の変換
点の位置を表すのに直交座標や極座標などいろいろな方法があることを学びました。それでは、再び直交座標系の話に戻ります。
突然ですが、以下のような座標の平行移動を考えてみましょう。ここでは簡単のために２次元座標で考えます。
座標系$\mathrm{O}_{x y}$（下図黒色）に対して新しい座標系を$\mathrm{O}^{\prime}_{x^{\prime} y^{\prime}}$（下図桃色）とします。座標系$\mathrm{O}^{\prime}_{x^{\prime} y^{\prime}}$が座標系$\mathrm{O}_{x y}$を $\vec{R}=(X,Y)$ だけスライドしたものだとすると、座標系$\mathrm{O}^{\prime}_{x^{\prime} y^{\prime}}$における原点$\mathrm{O}^{\prime}$は、元の座標系では$(X,Y)$となります。
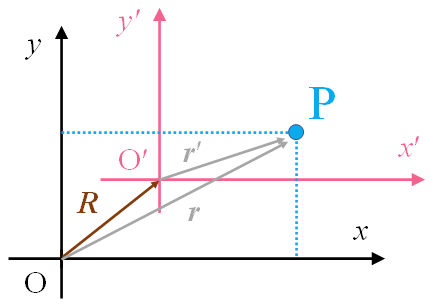図．座標の平行移動
このとき、座標系$\mathrm{O}_{x y}$の点$\mathrm{P}(x,y)$が座標系$\mathrm{O}^{\prime}_{x^{\prime} y^{\prime}}$において$(x^{\prime},y^{\prime})$として表されるとすると、$$x^{\prime}=x-X, \,y^{\prime}=y-Y$$という関係が成り立ちます。これはベクトル表示にすると$$\boldsymbol{r}^{\prime}=\boldsymbol{r}-\boldsymbol{R}$$と書き表せます（※式中の斜体の太字はベクトルを表しています）。
これはあくまでも座標系を変換しているだけで、物理的に点$\mathrm{P}$の位置が変化している訳ではないことに注意して下さい。「座標軸の平行移動」という数学的な操作を施すと座標の表示が変わるというだけの話です。
座標軸の平行移動以外にも、座標軸の回転操作も考えることができますが、やや複雑な内容なので今回は説明を省きます。
さて、何故わざわざこのようなややこしいことを考えるのかと言うと、物体の運動を記述する上で座標系の取り方が非常に重要だからです。
例えばボールを放り投げる運動（放物運動）の場合、普通は座標を地面に平行な向きに$x$軸、垂直な向きに$y$軸をとります（下図の黒い座標軸）。なぜなら、ボールに働く重力と同じ向きに軸をとった方が運動を考えやすい（記述しやすい）からです。
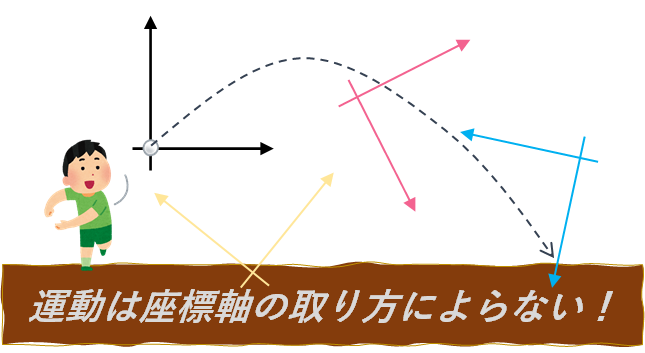図．座標軸の取り方はいろいろ
一般に、どこを座標系の原点（基準の位置）にしても物体の運動は変化しません。所詮、座標系というものは人間の頭の中にしかない存在なので、座標軸を平行移動しようが回転させようが、物体の運動そのものには何の影響も与えないのです。
※ この事実は「物体の運動は基準系によらない」などと表現できます。
物体の運動そのものは不変なので、力学の問題では座標系を任意に（＝どんな風にでも）設定することができます。物体と一緒に運動する座標系を考えることだってできます。だったら問題が解きやすくなるように座標系を設定するのはとても自然ですよね？
そういう訳で、物理（特に力学）の問題を解く上では、うまい座標の取り方が重要です。初めのうちはどんな風に座標系を決めればよいのか分からないかもしれませんが、基本的には問題が簡単になるように（運動方程式がシンプルになるように）設定します。色々な問題を解くうちに慣れてくるはずです。
※ 数学で「ベクトル」を履修済みの方であれば、上記の座標系の変換の話が「位置ベクトル」をちょっと仰々しく扱っているだけのことだと理解できると思います。位置ベクトルの考え方は「どこを基準点に取っても系内の点の相対的な位置関係を記述できる」というもので、見方を変えれば座標系の変換そのものです。
※ ところで、2022年度から施行される新課程ではベクトルが数Bから数Cに移されるため、いわゆる文系の学生はベクトルという概念に触れることなく高校を卒業してしまいます。データ科学関連の分野を増強するのは歓迎すべきことですが、ベクトルを追いやってまですることなのか疑問が湧きます。これは数Cの分量が増えて理系学生が忙しくなるのも問題なのですが、文系学生がベクトルを全く学ばなくなることで物理を専攻する機会を損なうのではないかということが危惧されます。もともと物理を専攻する文系学生が少ないとはいえ、これまで以上に物理に縁の無い学生が増えてしまいかねない文科省の改定にはやや残念です。