有機化合物の構造解析~IR編~
$\require{mhchem}$
IRとは?
IRとは、赤外吸収分光法 (infrared absorption spectrometry) の略称で、試料に赤外線を照射して得られる吸収スペクトルを測定する分析法のことを指します。この方法では、有機化合物に含まれている官能基に関する情報をスペクトルデータとして手っ取り早く得ることができます。
原子同士の結合は一定の長さに固定されている訳ではなく、バネのように絶えず振動しています。結合の振動には伸縮と変角の2種類が存在します。2原子分子では言わば「線的」な伸縮振動のモードしか存在しませんが、3個以上の原子を含む分子では「面的」な振動モードである変角振動のモードが現れます。
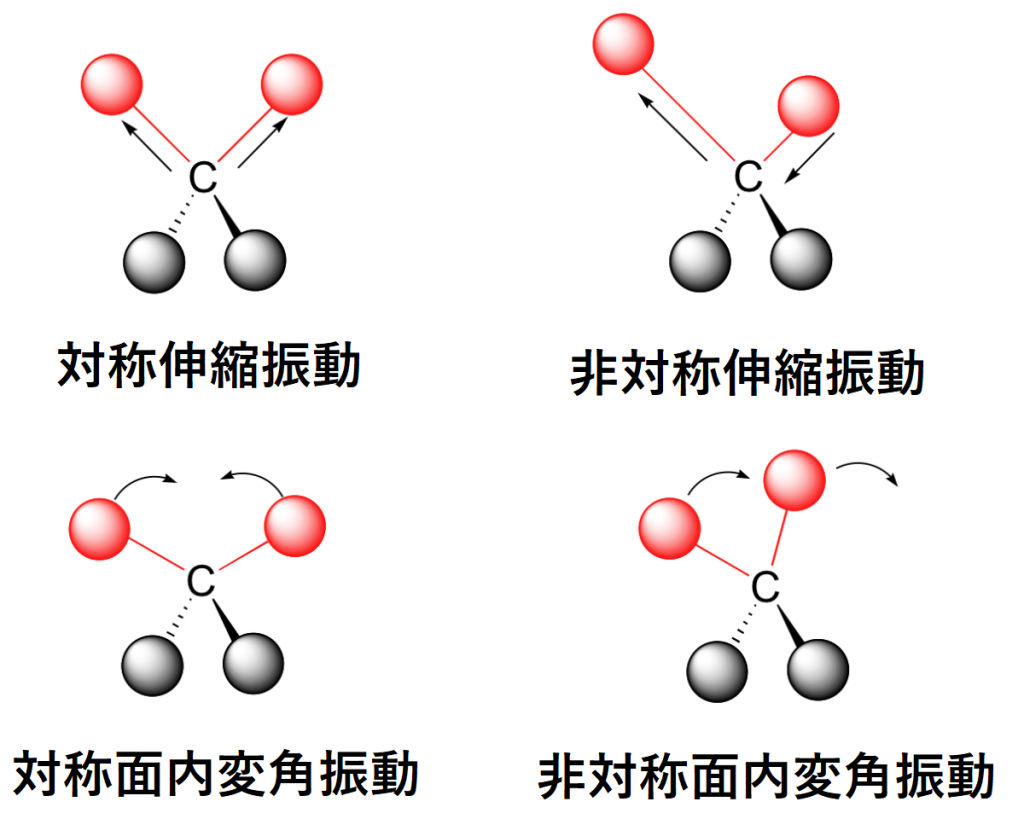
図1.振動様式の概念図
上の図1では4種類の振動モードしか示していませんが、変角振動には「面内」のほかに「面外」の変角振動モードが存在します。対称面内変角振動は「はさみ振動」、非対称面内変角振動は「縦揺れ振動」とも呼ばれ、対称面外変角振動は「ひねり振動」、非対称面外変角振動は「横揺れ振動」という用語で呼ばれることもあります。面に関してどういう位置関係の振動なのかによって振動モードが異なります。
このように分類される振動モードはいずれも特定の振動数をもち、その振動数に一致する周波数の電磁波を照射すると分子にエネルギーを与えることができます。これは、ブランコに乗っている人を後ろから上手い具合に押してあげると、より高いところまでブランコが振れるのと原理的には同じです。分子の振動運動の場合、赤外線がちょうどそのような周波数の電磁波に対応しているのです。
分子に赤外線を照射してあげると、ある一定の周波数の赤外線だけが吸収されるため、赤外線の透過率を測定すればどの周波数の赤外線が吸収されたのかを調べることができます。このようにして分子がどのような振動モード・結合をもつのかを調べるのが赤外吸収分光法の理屈です。
複数の原子からなる多原子分子だと振動モードの数も膨大です。それらすべての振動モードをスペクトルデータから解析し、帰属するのはプロでもなかなか難しいことです。そこで学部レベルではまず対象分子がどのような官能基を有するのかを決定する、若しくはヒントを得るための考え方を学ぶことになります。
基準振動の数について
分子の実体は3次元の構造をもつ原子の集団であり、$N$個の原子からなる分子の場合、その運動の自由度は$3N$となります。ただし$3N$個の原子は全く独立というわけではありません。分子全体は一体となって並進運動しており、これに必要な自由度は$3$です。また、分子には重心を中心とした回転運動も存在し、その自由度は直線分子で$2$、非直線分子では$3$となります。
残る $3N-6$(直線分子なら $3N-5$ )の自由度が振動運動を定める自由度となるので、$N$原子分子には全部で $3N-6$ 個(直線分子なら $3N-5$ 個)の振動モードが存在します。例えば$\ce{H2O}$の場合、原子数が$3$で非直線分子なので振動モードは全部で $3 \times 3 -6=3$ 個存在します。
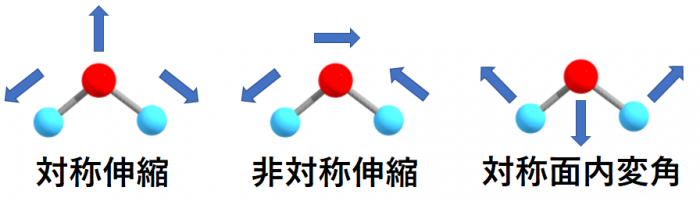
図2.水の振動モード
一方、$\ce{CO2}$の場合は同じく原子数が$3$ですが、こちらは直線分子なので振動モードは全部で $3 \times 3 -5=4$ 個存在します。
※二酸化炭素の振動モードのうち、結合方向を$x$軸とすると、変角振動は$y$軸方向、$z$軸方向の2種類があり、いずれも対称面内変角振動に分類されます。この2種類の変角振動は見た目上、区別が付きませんが、自由度(次元)の観点で考えることで異なる振動モードに分けられます。
IRスペクトルを読む!
結合の次数や極性などによって、スペクトルのピークを与える振動数やピークの形状が変わります。官能基はそれぞれ特徴的なIRスペクトルを与えるため、どのようなピークが現れているかを調べることで官能基を特定したり、絞り込んだりすることができます。
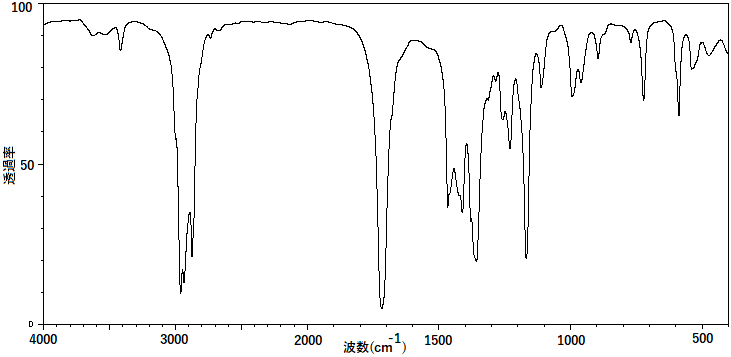
まずは2-ヘキサノンのIRスペクトル(液膜法)を例にスペクトルデータの見方について説明します。
横軸が波数(単位は$\mathrm{cm}^{-1}$)、縦軸が赤外線の透過率(%)です。赤外線の波長はおよそ$2.5\mathrm{μm}〜25\mathrm{μm}$程度の範囲なので、波数(=波長の逆数)に直すと大体$400\mathrm{cm}^{-1}〜4000\mathrm{cm}^{-1}$の範囲に収まります。実際にスペクトルデータの横軸はそのようにスケールされています。
透過率が下に尖って落ち込んでいるところを「ピーク」と呼びます。この例では$2900\mathrm{cm}^{-1}$や$1700\mathrm{cm}^{-1}$付近に鋭いピークが見られ、$1500\mathrm{cm}^{-1}$以下の領域では複数のピークが重なって少し複雑になっていることが分かります。
2-ヘキサノンは$$\ce{CH3-(CH3)3-CO-CH3}$$という構造のケトンであり、$\ce{C=O}$の二重結合と$\ce{C-C}$、$\ce{C-H}$の単結合を有します。それぞれの伸縮振動を帰属すると以下のようになります。
$2900\mathrm{cm}^{-1}$付近に見られるピークは$\ce{C-H}$伸縮振動によるもので、$1700\mathrm{cm}^{-1}$付近に見られるピークは$\ce{C=O}$伸縮振動によるものです。なお、$1500\mathrm{cm}^{-1}$以下の領域はスペクトルが複雑であり、それぞれのピークを帰属することが困難です。この領域は「指紋領域」と呼ばれ、立体構造や分子に固有のスペクトルが現れます。指紋領域からは官能基の判別は困難ですが、化合物の同定などに利用することができます。指紋領域に対して、$1500\mathrm{cm}^{-1}$以上の領域は「診断領域」と呼ばれます。
IRの結果を構造決定に利用する際は、主にこの「診断領域」のスペクトルデータを調べることになります。
特徴的なピークを探そう
特徴のあるピークを与える官能基(特性基)を知っておかなければIRスペクトルを取る意味がありません。IRは特にヘテロ原子を含む特性基や多重結合の有無を確かめるのに有用です。
以下に「診断領域」に現れるスペクトルの特徴を列挙します。
$1500~1800\mathrm{cm}^{-1}$付近は$\ce{C=O}$や$\ce{C=N}$、$\ce{C=C}$などの二重結合の伸縮振動に由来する吸収帯となっており、この周辺にピークがあれば対象分子は二重結合を有する可能性が高まります。芳香環を持つ場合は$1500~1600\mathrm{cm}^{-1}$付近にピークが見られます。また、特に$1700\mathrm{cm}^{-1}$付近に鋭いピークが見られる場合はカルボニル化合物の可能性が高いと言えます。
$1900~2800\mathrm{cm}^{-1}$(人によっては下限を$1800\mathrm{cm}^{-1}$、上限を$2500\mathrm{cm}^{-1}$とする場合があります)の領域は特に目立ったピークが観測されないため「不毛な領域」などと呼ばれることがあります。ただし対象としている化合物が三重結合を有する場合、若しくは、$\ce{N=C=O}$や$\ce{N=C=S}$、$\ce{N=C=N}$という構造を有する場合は、この領域にも$2100~2300\mathrm{cm}^{-1}$の範囲でピークが現れます。このことを覚えておくと構造決定の際に便利です。
$3000\mathrm{cm}^{-1}$周辺、前後$200\mathrm{cm}^{-1}$の領域には$\ce{C-H}$伸縮振動に由来するピークが現れますが、大抵の有機化合物はアルキル鎖をもっているため、官能基の識別にはあまり有用ではありません。単結合の伸縮振動に由来するピークで有用なものは$3200\mathrm{cm}^{-1}$より高波数側に現れます。特に$\ce{O-H}$伸縮振動は$3200~3500\mathrm{cm}^{-1}$の範囲に幅広い(ブロードな)ピークをもつため識別が容易です。
その他、高波数の領域には$\ce{N-H}$伸縮振動に由来する、$\ce{O-H}$伸縮振動に比べてやや鋭いピークが現れます。$\ce{N-H}$伸縮振動のピークは弱いことが多いため見逃しがちですが、窒素を含む組成の場合はこの領域にも注目すべきです。
これで診断領域に特徴的で重要なスペクトルについては一通り解説したことになります。IRで得られる情報からは構造に関する正確な情報まで引き出すのは難しいですが、少なくとも官能基に関する情報はキャッチできるようにしておくべきでしょう。
一つ、補足すべき点があります。赤外分光法では双極子モーメントが変化する振動の吸収を調べるため、対称な分子など、双極子モーメントが変化する振動モードをもたない分子は赤外不活性となってしまいます。逆に考えると、対象としている化合物が赤外不活性でIRスペクトルがうまく観測できない場合、その化合物は対称性を有することが示唆されます。
ともかく、IRは有機分子の官能基決定において非常に強力なツールとなります。スペクトルデータの読み方は是非ともマスターしておきたいですね!