反応速度論：逐次反応と定常状態
逐次反応の反応速度
逐次反応の場合を考察してみよう。次のような反応様式を「逐次反応」という。$$\mathrm{A} \overset{k_1}{\to} \mathrm{B} \overset{k_2}{\to} \mathrm{P} \tag{5.1}$$一次反応では$\mathrm{A}$から直接、生成物$\mathrm{P}$へ変化していたのに対して、逐次反応では中間体$\mathrm{B}$を経由して進行する。
$\mathrm{A}$の濃度変化は一次反応なので、反応速度定数を$k_1$とすると$$[\mathrm{A}]=[\mathrm{A}]_{0}e^{-k_1 t}\tag{5.2}$$が得られる。中間体$\mathrm{B}$の場合、消費される速さと生成する速さはそれぞれ$k_2[\mathrm{B}]$、$k_1[\mathrm{A}]$であるから、中間体$\mathrm{B}$の濃度の時間変化は$$-\dfrac{d[\mathrm{B}]}{dt}=k_2[\mathrm{B}]-k_1[\mathrm{A}]\tag{5.3}$$となり、$(5.2)$式を用いると$$-\dfrac{d[\mathrm{B}]}{dt}=k_2[\mathrm{B}]-k_1[\mathrm{A}]_{0}e^{-k_1 t}\tag{5.4}$$となる。
これは$$\dfrac{dy}{dx}+P(x)y=Q(x)\tag{5.5}$$という形の非同次形の$1$階線形微分方程式であり、高校数学のレベルを超えているので解の導出についてここでは触れない。解析学の知識より、$(5.5)$式の一般解は以下の形で与えられることが知られている。$$y=e^{-\int P(x)dx}\left(\int Q(x)e^{\int P(x)dx}dx+C\right)\tag{5.6}$$ $(5.5)$式において$x$を$t$と置き換え、$y$を$[\mathrm{B}]$、$P(x)$を$k_2$、$Q(x)$を$k_1[\mathrm{A}]_{0}e^{-k_1 t}$とすると、$$\begin{align}[\mathrm{B}]&=e^{-\int^{t}_{0} k_2\,dt}\left(\int^{t}_{0} k_1[\mathrm{A}]_{0}e^{-k_1 t}\cdot e^{\int^{t}_{0} k_2\,dt}dt\right) \\ &=e^{-k_{2}t}\int^{t}_{0} k_1[\mathrm{A}]_{0}e^{(k_2-k_1)t}dt \\ &=k_1[\mathrm{A}]_{0}e^{-k_{2}t}\left[\dfrac{1}{k_2-k_1}e^{(k_2-k_1)t}\right]^{t}_{0} \\ &=k_1[\mathrm{A}]_{0}e^{-k_{2}t}\left(\dfrac{e^{(k_2-k_1)t}}{k_2-k_1}-\dfrac{1}{k_2-k_1}\right) \\ &=\dfrac{k_1[\mathrm{A}]_{0}}{k_2-k_1}(e^{-k_{1}t}-e^{-k_{2}t}) \tag{5.7}\end{align}$$と求められる。ただし、積分の過程で$\mathrm{B}$の初濃度を$0$とした。
生成物$\mathrm{P}$の初濃度が$0$のとき、逐次反応においては以下の関係式が成り立つ。$$[\mathrm{A}]+[\mathrm{B}]+[\mathrm{P}]=[\mathrm{A}]_{0}\tag{5.8}$$これより生成物$\mathrm{P}$の濃度は$$[\mathrm{P}]=[\mathrm{A}]_{0}\left(1+\dfrac{k_{1}e^{-k_{2}t}-k_{2}e^{-k_{1}t}}{k_2-k_1}\right)\tag{5.9}$$と求められる。
図７．逐次反応における濃度の時間変化
グラフを見て分かる通り、$[\mathrm{P}]=[\mathrm{A}]$ となる時刻で$[\mathrm{B}]$が極大となるが、これは数学的に導出可能である。
また、$k_1=k_2$ のときは$(5.7)$式を直接使うことはできないが、微分法の知識を使えば式変形が可能である。$(5.7)$式において $k_2=k_1+h$ と置き、極限 $h \to 0$ を取れば導関数の定義から新たな式を導くことができる。$k_2=k_1+h$ と置くとき、$(5.7)$式より、$$\begin{align}[\mathrm{B}]&=k_1[\mathrm{A}]_{0}\dfrac{e^{-k_{1}t}-e^{-(k_{1}+h)t}}{h} \\ &=-k_1[\mathrm{A}]_{0}\dfrac{e^{-t(k_{1}+h)}-e^{-tk_{1}}}{h} \\ &\overset{(h \to \infty)}{\to} -k_1[\mathrm{A}]_{0}\left(\dfrac{d}{dk_1}e^{-tk_{1}}\right) \\ &= k_1[\mathrm{A}]_{0}te^{-k_{1}t} \tag{5.10}\end{align}$$を得る。故に $k_1=k_2$ のとき、生成物$\mathrm{P}$の初濃度が$0$であれば濃度$[\mathrm{P}]$は$$[\mathrm{P}]=[\mathrm{A}]_{0}\left(1-e^{-k_1 t}-k_1te^{-k_{1}t}\right)\tag{5.11}$$と表せる。
逆反応が存在する場合
逆反応がある場合の反応式は次のように表される。$$\mathrm{A} \underset{k_{b}}{\overset{k_{f}}{\rightleftarrows}} \mathrm{B}\tag{6.1}$$逆反応を無視できない場合、$\mathrm{A}$、$\mathrm{B}$に関する微分方程式は以下のように表すことができる。$$\begin{cases}-\dfrac{d[\mathrm{A}]}{dt}=k_f[\mathrm{A}]-k_b[\mathrm{B}] \\ -\dfrac{d[\mathrm{B}]}{dt}=k_b[\mathrm{B}]-k_f[\mathrm{A}] \end{cases}\tag{6.2}$$ $\mathrm{A}$、$\mathrm{B}$の初濃度をそれぞれ$[\mathrm{A}]_{0}$、$0$とするとそれぞれの濃度の間に$$[\mathrm{B}]+[\mathrm{A}]=[\mathrm{A}]_{0}\tag{6.3}$$という関係式が成り立つため、これより$[\mathrm{B}]$を消去すると微分方程式は以下のように書き直せる。$$-\dfrac{d[\mathrm{A}]}{dt}=(k_f+k_b)[\mathrm{A}]-k_b[\mathrm{A}]_{0}\tag{6.4}$$これも前節と同様、非同次形の$1$階線形微分方程式であるので、$(5.6)$式から$$[\mathrm{A}]=[\mathrm{A}]_{0}\left(\dfrac{k_f}{k_f+k_b}e^{-(k_{f}+k_{b})t}+\dfrac{k_b}{k_f+k_b}\right)\tag{6.5}$$を得る。よって$\mathrm{B}$についても$$[\mathrm{B}]=[\mathrm{A}]_{0}\left(-\dfrac{k_f}{k_f+k_b}e^{-(k_{f}+k_{b})t}+\dfrac{k_f}{k_f+k_b}\right)\tag{6.6}$$と求められる。
これより、十分長い時間が経過した後の$\mathrm{A}$と$\mathrm{B}$の濃度比$\dfrac{[\mathrm{B}]_{\infty}}{[\mathrm{A}]_{\infty}}$は$$\dfrac{[\mathrm{B}]_{\infty}}{[\mathrm{A}]_{\infty}}=\dfrac{k_f}{k_b}\tag{6.7}$$に収束することが分かる。
また、反応初期においては逆反応がある場合でも$\mathrm{A}$の一次反応に近似することができる。これは$(6.5)$式の $t=0$ 近傍におけるテイラー展開（＝マクローリン展開）を考えれば理解できるであろう。
律速段階と定常状態近似
化学反応が複数の素反応からなっている場合、全体の反応速度は最も遅い素反応によって決定される。全体の反応速度を決定する最も遅い反応のことを「律速段階」や「律速過程」、あるいは「ボトルネック」などと呼ぶ。
逐次反応の場合を例に考えよう。先ほど、反応速度は以下のようになることを確かめた。$$[\mathrm{P}]=[\mathrm{A}]_{0}\left(1+\dfrac{k_{1}e^{-k_{2}t}-k_{2}e^{-k_{1}t}}{k_2-k_1}\right)\tag{5.9}$$これにおいて $\mathrm{B}\to\mathrm{P}$ の反応が律速段階であるとすると、$k_1 \gg k_2$ より、$\dfrac{k_2}{k_1} \approx 0$ となるので$(5.9)$式は$$[\mathrm{P}]=[\mathrm{A}]_{0}\left(1-e^{-k_{2}t}\right)$$と変形できる。これは２番目の反応によって全体の反応速度が決定されていることを表している。
また、$\mathrm{A}\to\mathrm{B}$ の反応が律速段階であるとすると、$k_1 \ll k_2$ より、$\dfrac{k_1}{k_2} \approx 0$ となるので$(5.9)$式は$$[\mathrm{P}]=[\mathrm{A}]_{0}\left(1-e^{-k_{1}t}\right)$$と変形できる。これは１番目の反応によって全体の反応速度が決定されていることを表している。
この例からも分かる通り、律速段階を仮定に含めることによって反応速度を簡単に求めることができるようになる。律速段階を設定することにより、中間体の濃度に関して更に強力な近似が適用可能となる。そこで逆反応が存在する以下の反応系を考えよう。$$\mathrm{A} \underset{k_{-1}}{\overset{k_{1}}{\rightleftarrows}} \mathrm{B} \overset{k_{2}}{\to} \mathrm{P}\tag{7.1}$$ここで $\mathrm{B} \to \mathrm{P}$ の過程が律速段階であるとする。全体の反応速度は律速段階の速度に等しくなるので、全体の反応速度$r$は$$r=k_2[\mathrm{B}]\tag{7.2}$$と表せる。よって$[\mathrm{B}]$を求めれば全体の反応速度を決定することができる。
さて、中間体$\mathrm{B}$の濃度の時間変化について、以下の方程式が成立する。$$\dfrac{d[\mathrm{B}]}{dt}=k_{1}[\mathrm{A}]-k_{-1}[\mathrm{B}]-k_{2}[\mathrm{B}]\tag{7.3}$$ここで、$\mathrm{A} \rightleftarrows \mathrm{B}$ の反応は律速段階に比べて十分によく進むから、十分時間が経過すると中間体$\mathrm{B}$の濃度がほとんど変化しない状態に達する。これを「定常状態」と呼び、このとき $\dfrac{d[\mathrm{B}]}{dt}=0$ が成り立つ。これより$(7.3)$式から、$$k_{1}[\mathrm{A}]-k_{-1}[\mathrm{B}]-k_{2}[\mathrm{B}]=0\tag{7.4}$$という関係式が導かれる。これより$$[\mathrm{B}]=\dfrac{k_{1}}{k_{-1}+k_{2}}[\mathrm{A}]\tag{7.5}$$を得るので、$(7.2)$式より、$$r=\dfrac{k_{1}k_{2}}{k_{-1}+k_{2}}[\mathrm{A}]\tag{7.6}$$となる。これより、この反応はあたかも$\mathrm{A}$の一次反応のように振る舞うことが分かる。
このような近似は「定常状態近似」と呼ばれ、一見複雑な速度論のモデルをかなり単純化することができる。実は定常状態近似が考案されたのが1922年頃なので、百年も経っていない理論である。
酵素反応への応用
酵素反応でよく知られるミカエリス・メンテン機構に定常状態近似を応用する例を紹介して本稿を締めくくろう。
酵素反応では基質$\mathrm{A}$が酵素$\mathrm{E}$と錯体$\mathrm{AE}$を作り、これから生成物$\mathrm{P}$が得られる。酵素$\mathrm{E}$は触媒作用を示し、次の反応サイクルでも利用される。反応全体としては $\mathrm{A} \to \mathrm{P}$ という一次反応と言えるが、素反応別に書き表すと次のようになる。$$\mathrm{A}+\mathrm{E} \underset{k_{-1}}{\overset{k_{1}}{\rightleftarrows}} \mathrm{AE} \overset{k_{2}}{\to} \mathrm{P}+\mathrm{E}\tag{8.1}$$酵素反応においては生成物が生じる二番目の過程が律速段階となる。全体の反応速度は律速段階の速度に等しくなるので、全体の反応速度$r$は$$r=k_2[\mathrm{AE}]\tag{8.2}$$と表せる。よって$[\mathrm{AE}]$を求めれば全体の反応速度を決定することができる。
錯体$\mathrm{AE}$の濃度の時間変化は以下のようになる。$$\dfrac{d[\mathrm{AE}]}{dt}=k_{1}[\mathrm{A}][\mathrm{E}]-k_{-1}[\mathrm{AE}]-k_{2}[\mathrm{AE}]\tag{8.3}$$二番段階目が律速となるから$[\mathrm{AE}]$について定常状態近似が適用できて、$$k_{1}[\mathrm{A}][\mathrm{E}]-k_{-1}[\mathrm{AE}]-k_{2}[\mathrm{AE}]=0\tag{8.4}$$を得る。これより定常状態の$\mathrm{AE}$の濃度は$$[\mathrm{AE}]=\dfrac{k_{1}}{k_{-1}+k_{2}}[\mathrm{A}][\mathrm{E}]\tag{8.5}$$と求められ、$K_\mathrm{M}=\dfrac{k_{-1}+k_{2}}{k_{1}}$ とミカエリス定数で表せば、$$[\mathrm{AE}]=\dfrac{1}{K_\mathrm{M}}[\mathrm{A}][\mathrm{E}]\tag{8.6}$$と書き改めることができる。
酵素反応において、酵素$\mathrm{E}$は触媒としてのみ働くため、酵素の全量は反応の前後で不変である。したがって酵素の初濃度を$[\mathrm{E}]_{0}$と置けば、$$[\mathrm{E}]_{0}=[\mathrm{E}]+[\mathrm{AE}]\tag{8.7}$$となる。これより$(8.6)$式から$[\mathrm{E}]$を消去すると$$[\mathrm{AE}]=\dfrac{[\mathrm{E}]_{0}}{1+K_\mathrm{M}/[\mathrm{A}]}\tag{8.8}$$を得るので、$(8.8)$式を$(8.2)$式に代入して$$r=\dfrac{k_{2}[\mathrm{E}]_{0}}{1+K_\mathrm{M}/[\mathrm{A}]}\tag{8.9}$$と求めることができる。
$(8.1)$式のように進行する反応機構を「ミカエリス・メンテン機構」といい、$(8.9)$式を「ミカエリス・メンテンの式」と呼ぶ。$(8.5)$式を変形すると$$K_\mathrm{M}=\dfrac{[\mathrm{A}][\mathrm{E}]}{[\mathrm{AE}]}\tag{8.10}$$となるので、ミカエリス定数は錯体$\mathrm{AE}$の解離平衡定数と解釈することができる。
基質$\mathrm{A}$の濃度が大きく、$[\mathrm{A}]\gg K_\mathrm{M}$ となるときは $\dfrac{K_\mathrm{M}}{[\mathrm{A}]}\approx 0$ と近似でき、このとき反応速度は最大となる。これを$r_{\mathrm{max}}$と置くと$$r_{\mathrm{max}}=k_{2}[\mathrm{E}]_{0}\tag{8.11}$$と表せるので、$(8.9)$式より、$$r=\dfrac{r_{\mathrm{max}}}{1+K_\mathrm{M}/[\mathrm{A}]}\tag{8.12}$$ $$\therefore \dfrac{1}{r}=\dfrac{1}{r_{\mathrm{max}}}+\dfrac{K_\mathrm{M}}{r_{\mathrm{max}}}\dfrac{1}{[\mathrm{A}]}\tag{8.13}$$と式変形できる。これより、反応速度の逆数を基質の濃度の逆数に対してプロットすることで、傾きが$\dfrac{K_\mathrm{M}}{r_{\mathrm{max}}}$、縦軸の切片が$\dfrac{1}{r_{\mathrm{max}}}$の直線が得られる。
こうした方法で得られたプロットは「ラインウィーバー＝バークプロット」と呼ばれ、生化学などの分野では酵素阻害の形式を決定する簡便な手法として知られている。ただし、この方法は逆数をプロットするという性質上、小さい値のずれであっても誤差が大きくなる場合があるため、現在では専ら非線形回帰法が利用されている。ラインウィーバープロット等の線形回帰法は学生実験などで扱われることが多い。
終わりに
これまで紹介してきた内容はあくまでも化学の教養知識に過ぎない。これよりも更に高度な内容として「遷移状態理論」があり、抽象化を突き進めるとほとんど数理物理学と言って差し支えないような分野に至る。
実際に速度論を理論的に扱う際はポテンシャルエネルギー曲面上での議論を持ち出すことが多く、主に活性化エネルギーの高低をもとに反応速度を計算することができる。
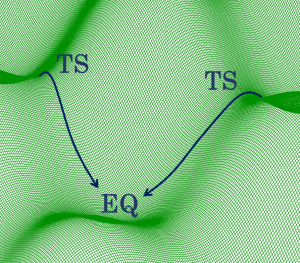図８．ポテンシャルエネルギー曲面の概念図
昨今の理論計算プログラムの飛躍的な発展によって反応の速度論的な解析はますます手軽になっており、化学反応を自動で追跡・探索することも可能になってきている。量子化学計算ソフトが充実した現代においては、フラスコだけでなくコンピュータも化学をする上で欠かせないツールとなっている。