フィボナッチ数列の問題
慶応義塾大学(1961年/(医)数学Ⅰ代数)
横浜国立大学(1964年/前期理系(工)第6問)
数列$x_1$、$x_2$、$\cdots$、$x_n$、$\cdots$の一般項の間に$$x_n+x_{n+1}=x_{n+2} \ \ \ (x_1=x_2=1)$$の関係があるとき、次の問いに答えよ。
(1)$$\begin{align}& x_{n+2}-\alpha x_{n+1}=\beta (x_{n+1}-\alpha x_{n}) \\ & x_{n+2}-\beta x_{n+1}=\alpha (x_{n+1}-\beta x_{n}) \end{align}$$のような定数${\alpha}$、${\beta} \ (\alpha \leqq \beta)$を決めよ。
(2)$x_{n+1}-\alpha x_{n}$ を${\beta}$で表わせ。また $x_{n+1}-\beta x_{n}$ を${\alpha}$で表わせ。次に$x_n$を$\alpha$、$\beta$で表わせ。
(3)$1+\displaystyle \sum_{k=1}^{\infty} x_k=x_p$ のとき、$p$を$n$で表わせ。
東京工業大学(1967年/第3問)
$C_0=1$、$C_1=1$、$C_{n+1}=C_{n}+C_{n-1} \ (n \geqq 1)$ で定義される数列$\{C_n\}$がある。2次方程式$$x^2-(C_{n+1}+C_{n-1})x+(C_{n+1}C_{n-1}-C_{n}^2)=0$$の2根を${\alpha}_n$、${\beta}_n$とする。ただし ${\alpha}_n \geqq {\beta}_n$ とする。このとき
(1)$\dfrac{{\alpha}_{n+1}}{{\alpha}_{n}}$、$\dfrac{{\beta}_{n+1}}{{\beta}_{n}}$を求めよ。
(2)${\alpha}_n$、${\beta}_n$を求めよ。
三重大学(1985年/理系(工)第1問)
広島大学(1985年/理系第2問-文系第4問)
$a_1=1$、$a_2=1$、$a_{n+2}=a_{n+1}+a_{n} \ (n \geqq 1)$ で定まる数列を$\{a_n\}$とする。次に、新しい数列$\{b_n\}$および$\{{\theta}_n\}$を$$\begin{align}& b_n=a_{n}a_{n+2}-a_{n+1}^2 \ (n \geqq 1)、\\ &\tan {\theta}_{n} = \dfrac{1}{a_n}、0<{\theta}_n<\dfrac{\pi}{2} \ (n \geqq 1) \end{align}$$によって定める。このとき、正の整数$n$に対して次の等式が成り立つことを示せ。
(1)$b_{n}+b_{n+1}=0$
(2)$a_{2n}a_{2n+2}-a_{2n+1}^2=-1$
(3)$\tan ({\theta}_{2n}-{\theta}_{2n+2})=\tan {\theta}_{2n+1}$
高知大学(1985年/理系(数)第5問)
北海道大学(1987年/前期文系(文Ⅱ/Ⅲ)第3問)
千葉大学(1990年/前期理系(数学)第6問)
大阪大学(1991年/後期理系(理)第1問)
東京大学(1992年/前期文系第3問)
三重大学(1992年/前期理系第?問)
大阪市立大学(1994年/後期理系(理)第3問)
数列$\{a_n\}$は、$$a_{n+2}=a_{n+1}+a_{n} \ (n=1,2,3,\cdots)$$を満たすとする。$b_n={a_n}^2+{a_{n+1}}^2$、$c_n=a_{2n}$ とおくとき、次の問に答えよ。
(1)関係式 $b_{n+2}-3b_{n+1}+b_n=0$ を示せ。
(2)$c_n$、$c_{n+1}$、$c_{n+2}$の間の関係式を求めよ。
京都大学(1994年/前期理系第4問/前期文理共通第2問)
$n$は$0$または正の整数とする。$a_n$を $a_0=1$、$a_1=2$、$a_{n+2}=a_{n+1}+a_{n}$ によって定める。$a_n$を$3$で割った余りを$b_n$とし、$c_n=b_0+\cdots+b_n$ とおく。
(1)$b_0$、$\cdots$、$b_n$を求めよ。
(2)$c_{n+8}=c_n+c_7$ であることを示せ。
(3)$n+1 \leqq c_n \leqq \dfrac{3}{2}(n+1)$ が成り立つことを示せ。
東北大学(1997年/前期文系第5問(選択))
(1)2次方程式 $x^2+ax+b=0$ が相異なる2つの解$\alpha$、$\beta$を持つとき、定数$p$、$q$に対し$$\begin{align} x_0=p+q、x_n=&p{\alpha}^2+q{\beta}^n \\ &(n=1,2,3,\cdots) \end{align}$$とおく。このとき次の等式が成り立つことを示せ。$$x_{n+2}+ax_{n+1}+bx_{n}=0 \ (n=0,1,2,\cdots)$$
(2)$x_0=2$、$x_1=3$、$x_{n+2}=x_{n+1}+x_{n} \ (n=0,1,2,\cdots)$ で与えられる数列の一般項は$$x_n=\dfrac{2+\sqrt{5}}{\sqrt{5}}\left(\dfrac{1+\sqrt{5}}{2}\right)^n+\dfrac{-2+\sqrt{5}}{\sqrt{5}}\left(\dfrac{1-\sqrt{5}}{2}\right)^n$$で与えられることを示せ。
東京大学(1998年/前期理系第3問)
京都府立医科大学(1998年/第3問)
※題意の数列はフィボナッチ数列ではなくリュカ数列。
熊本大学(1998年/(1A)第3問(選択))
$a_1=a_2=1$、$a_{n+1}=a_{n}+a_{n-1} \ (n \geqq 3)$ により定まる数列$\{a_n\}$について、つぎの問いに答えよ。
(1)$n=3$、$4、\cdots、9$に対して$a_n$の値を求めよ。
(2)$n$が$3$の倍数ならば$a_n$は偶数であり、$n$が$3$の倍数でなければ$a_n$は奇数であることを示せ。
東京大学(2001年/前期理系第4問)
横浜国立大学(2001年/後期(工)第4問)
数列$\{a_n\}$は$a_1=1$、$a_2=1$、$a_{n}a_{n+2}-a_{n-1}^2=(-1)^{n+1} \ (n=1,2,3,\cdots)$ により定まる。次の問いに答えよ。
(1)$a_{n+2}=a_{a+1}+a_{n}$ が成り立つことを証明せよ。
(2)$m$を自然数とするとき、$a_{6m}$は$8$の倍数であることを示せ。
名古屋大学(2001年/後期(工)第2問)
$a_1=1$、$a_2=1$、$a_{n+1}=a_{n}+a_{n-1} \ (n=2,3,4,\cdots)$ で定まる数列$\{a_n\}$に関して、つぎの各問に答えよ。
(1)$\displaystyle \sum_{n=2}^{\infty} \dfrac{a_n}{a_{n-1}a_{n+1}}$の値を求めよ。
(2)$n=1$、$2$、$3$のそれぞれについて、$$a_{2n+2}=a_{n+1}^2+2a_{n+1}a_n$$が成り立つことを確かめよ。さらに、$a_{2n+1}$を$a_{n+1}$、$a_n$で表す式を推測せよ。
(3)自然数$n$に関する1組の式$$\begin{cases} (2)\text{で推測した式} \\ a_{2n+2}=a_{n+1}^2+2a_{n+1}a_n \end{cases}$$がすべての自然数$n$に対して成り立つことを数学的帰納法を用いて証明せよ。
東京大学(2002年/前期文理共通第2問)
横浜市立大学(2003年/理系第4問)
名古屋市立大学(2006年/前期(医)第4問)
実数$p$、$q$に対して数列$\{a_{n}\}$が $a_1=1$、$a_2=p+q$、$a_{n+2}-(p+q)a_{n+1}+pqa_{n}=0$ を満たすとする。このとき次の問いに答えよ。
(1)$a_{n}$を$p$、$q$、$n$で表せ。
(2)$p$、$q$が方程式 $x^2-x-1=0$ の$2$つの解とする。すべての自然数$m$、$n$に対して$$a_{m+n+1}=a_{m+1}a_{n+1}+a_{m}a_{n}$$成り立つことを示せ。
(3)(2)のとき、$n$が$5$の倍数ならば$a_{n}$も$5$の倍数であることを示せ。
大阪市立大学(2006年/後期理系(工/数)第1問)
※行列との融合問題。
京都大学(2007年/理系第1問(問1))
$1$歩で$1$段または$2$段のいずれかで階段を昇るとき、$1$歩で$2$段昇ることは連続しないものとする。$15$段の階段を昇る昇り方は何通りあるか。
岡山大学(2010年/理系第2問)
※リュカ数列の問題。
青山学院大学(2012年/経済第?問)
数列$\{a_n\}$の一般項 $a_n=\dfrac{1}{\sqrt{5}}\left\{\left({\dfrac{1+\sqrt{5}}{2}}\right)^{n}-\left({\dfrac{1-\sqrt{5}}{2}}\right)^{n}\right\}$ の$a_{3}$、$a_{7}$、$a_{12}$を答えよ。
愛知県立大学(2012年/情報科第2問)
※図形(正五角形)を題材とした問題。
芝浦工業大学(2012年/後期第4問)
会談を1歩で登るのが1段または2段であるような登り方をするとき、$n$段目($n=1,2,3,\cdots$)までの登り方の総数を$a_n$とする。次の問いに答えよ。
(1)数列$\{a_n\}$は漸化式 $a_{n+2}=a_{n+1}+a_{n}$ $(n=1,2,3,\cdots)$ を満たすことを示せ。
(2)${a_1}^2+{a_2}^2+\cdots+{a_n}^2=a_n a_{n+1}-1$ であることを示せ。
(3)2次方程式 $x^2=x+1$ の2つの解を$\alpha$、$\beta$(ただし、$\alpha>\beta$)とする。数列$\{b_n\}$、$\{c_n\}$をそれぞれ $b_n=a_{n+1}-\alpha a_n$、$c_n=a_{n+1}-\beta a_n$ と定めたとき、$b_n$、$c_n$がそれぞれ
$b_{n+1}=\beta b_n、c_{n+1}=\alpha c_n$ $(n=1,2,3,\cdots)$
を満たすことを示せ。
(4)(3)を用いて、$$a_n=\dfrac{1}{\sqrt{5}}({\alpha}^{n+1}-{\beta}^{n+1})$$であることを示せ。
京都府立医科大学(2013年/第2問)
数列$\{a_n\}$は $a_1=a_2=1$ かつ漸化式$$a_{n+2}=a_{a+1}+a_{n} \ (n=1,2,3,\cdots)$$を満たすものとする。自然数$n$に対して、実数${\theta}_{n}$を
$0<{\theta}_n<\dfrac{\pi}{2}$ かつ $\tan {\theta}_{n} = \dfrac{1}{a_n}$
となるように定める。
(1)$a_{n}(a_{n+2}+a_{n+1})=a_{n+2}a_{n+1}-(-1)^n$ $(n=1,2,3,\cdots)$ が成り立つことを証明せよ。
(2)${\theta}_{2k+1}+{\theta}_{2k+2}={\theta}_{2k} \ (k=1,2,3,\cdots)$ が成り立つことを証明せよ。
(3)$\displaystyle \sum_{k=1}^{\infty} {\theta}_{2k-1}$ を求めよ。
京都大学(2015年6月/特色入試サンプル試験問題第4問)
次のような数列 $a_1、a_2、\cdots$ を考える。
$a_{n+2} = a_{n+1} + a_{n}$ $(n \geqq 1)$、$a_1 = 1$、$a_2 = 1$
$m \geqq 6$ とし、$a_m$ は素数であるとする。$k = (a_m)^2$ とおく。整数 $b_n$、$c_n$ を
$(1 + \sqrt{5})^n = b_n + c_n \sqrt{5}$
が成り立つように定める。以下の設問に答えよ。
1. $c_n$ を $a_n$ を用いて表わせ。
2. $b_{k} − 1$ と $c_k − 1$ は $a_m$ で割り切れることを示せ。
3. $k − 1$ は $m$ で割り切れることを示せ。
埼玉大学(2015年/前期理系第1問)
東京大学(2015年/第4問)
数列$\{p_n\}$を次のように定める。
$p_1=1$、$p_2=2$、$p_{n+2}=\dfrac{{p_{n+1}}^2+1}{p_n} \ (n=1,2,3,\cdots)$
(1)$\dfrac{{p_{n+1}}^2+{p_n}^2+1}{p_{n+1}p_n}$が$n$によらないことを示せ。
(2)すべての $n=2,3,4,\cdots$ に対し、$p_{n+1}+p_{n-1}$を$p_n$のみを使って表せ。
(3)数列$\{q_n\}$を次のように定める。
$q_1=1$、$q_2=1$、$q_{n+2}=q_{n+1}+q_n \ (n=1,2,3,\cdots)$
すべての $n=1,2,3,\cdots$ に対し、$p_n=q_{2n−1}$を示せ。
新潟大学(2015年/推薦理学部数学科第2問)
大阪医科大学(2015年/前期第2問)
藤田保健衛生大学(2015年/前期(医)第5問)
※関数列の問題
大阪大学(2016年/前期専門数学第1問)
島根大学(2016年/(理工数理/情報システム)第1問)
鹿児島大学(2016年/前期(共通)大問3-第1問(選択))
北里大学(2016年/理(物理/化/生物科)第3問(1))
九州工業大学(2017年/情報工/工/前期第4問)
数$1$と数$2$の並びを考える。たとえば、$1$、$2$、$1$の順の並びを$(1,2,1)$で表す。和が自然数$n$となるような数$1$と数$2$の並びの集合を$S_n$と表し、$S_n$の要素の個数を$a_n$とする。たとえば、$n=3$ のとき、$3=2+1=1+2=1+1+1$ となるので、$S_3={(2,1),(1,2),(1,1,1)}$、$a_3=3$ となる。次に答えよ。
(ⅰ) $a_4$および$a_5$を求めよ。
(ⅱ) $a_{n+2}$を$a_{n+1}$と$a_{n}$で表せ。
(ⅲ) $\displaystyle \sum_{i=1}^{n} a_i=a_{n+2}−2$ となることを示せ。
(ⅳ) $S_{n+3}$から並びを一つ選ぶとき、その並びの$1$番目の数が$1$となる確率を$a_{n+1}$と$a_{n+2}$を用いて表せ。
(ⅴ) $S_{n+3}$から並びを一つ選ぶとき、その並びの$2$番目の数が$2$となる確率を$a_{n+1}$と$a_{n+2}$を用いて表せ。
(ⅵ) $S_{n+4}$から並びを一つ選ぶ。選んだ並びの$2$番目の数が$2$であるとき、その並びの$1$番目の数が$1$である確率を$a_{n+1}$と$a_{n+2}$を用いて表せ。
早稲田大学(2017年/(スポーツ科学部)第1問)
近畿大学(2017年/医学部推薦第?問)
立命館大学(2017年/理系第3問)
※図形との融合題
九州大学(2017年/理(数)/工/後期理系第5問)
次の条件によって定められる数列$\{a_n\}$がある。
$a_1=1$、$a_2=1$、$a_{n+2}=a_{n+1}+a_n \ (n=1,2,3,\cdots)$
以下の問いに答えよ。
(1) $2$ 以上の自然数 $n$ に対して、$a_{n+2}>2a_n$ が成り立つことを示せ。
(2)$2$ 以上の自然数 $m$ は、数列$\{a_n\}$の互いに異なる $k$ 個 $(k \geqq 2)$ の項の和で表されることを、数学的帰納法によって示せ。
(3)(2)における項の個数 $k$ は、$k<2\log_2 m+2$ を満たすことを示せ。
京大実戦(2017年/第2回理系第3問(駿台))
※$a_1=1$、$a_2=a$、$a_{n+2}=a_{n+1}+a_n \ (n=1,2,3,\cdots)$ のとき、ある項がある項の2倍に等しくなるように定数$a$を定める問題。(著作権の関係で全文の掲載は控えさせて頂きます)
立教大学(2018年/理系(理)第4問)
東京医科歯科大学(2018年/第1問)
東大プレ(2018年/第1回文理第4問(代ゼミ))
※$a_1=1$、$a_2=2$、$a_{n+2}=a_{n+1}+a_n \ (n=1,2,3,\cdots)$ のとき、$5(a_{2n})^2-4$ が平方数であることの証明問題。(著作権の関係で全文の掲載は控えさせて頂きます)
北海道大学(2019年/前期文系第3問)
$n$を自然数とする。数列 $2,1,2,1,1$ のように各項が$1$または$2$の有限数列(項の個数が有限である数列)を考える。各項が$1$または$2$の有限数列のうちすべての項の和が $n$ となるものの個数を $s_n$ とする。例えば、$n=1$ のときは、$1$項 からなる数列$1$のみである。したがって、$s_1 = 1$ となる。$n=2$ のときは、$1$項からなる数列$2$と$2$項からなる数列$1,1$の$2$つである。したがって、$s_2 = 2$ となる。
(1)$s_3$を求めよ。
(2)$n \geqq 3$ のとき, $s_n$を$s_{n-1}$と$s_{n-2}$を用いて表せ。
(3)$3$以上のすべての$n$に対して $s_{n}-\alpha s_{n-1} = \beta (s_{n-1} – \alpha s_{n-2})$ が成り立つような実数 $\alpha,\,\beta$ の組$(\alpha,\,\beta)$を$1$組求めよ。
(4)$s_n$を求めよ。
滋賀大学(2020年/前期文系第1問)
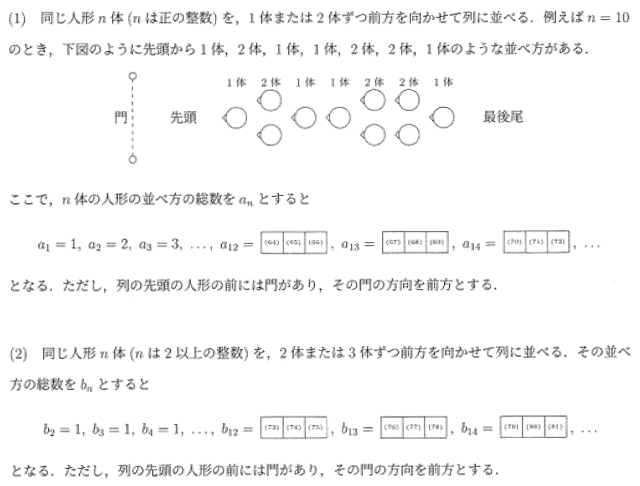
慶應義塾大学(2021年/(総合政策)第5問)
浜松医科大学(2021年/前期第3問)
階段を一度に1段登る、または1段飛ばして登る登り方をするとき、$n$段目までの登り方の総数を$a_n$とする。例えば、$a_1=1$、$a_2=2$、$a_3=3$ である。以下の問いに答えよ。
(1)$n$を$3$以上の整数とする。$n-1$段を踏む$n$段目までの登り方の総数を$b_n$、$n-1$段目を踏まない$n$段目までの登り方の総数を$c_n$とする。$b_n$、$c_n$を$a_1$、$a_2$、$\cdots$、$a_{n-1}$を用いて表せ。
(2)極限値$\displaystyle\lim _{n \rightarrow \infty} \frac{a_{n+1}}{a_{n}}$が存在することを認めて、この極限値を求めよ。
(3)$n$を$2$以上の整数とするとき、等式$$a_{2 n}=a_{n}^{2}+a_{n-1}^{2}$$が成立することを示せ。
信州大学(2022年/(医)第5問)
$a_1=a_2=1$ を満たす数列$\{a_n\}$について,次の2つの条件 $p$ と $q$ が同値であることを示せ.
$p$:すべての自然数$n$に対して,$a_{n+2}=a_{n+1}+a_{n}$ が成り立つ.
$q$:すべての自然数$n$に対して,$a_{n+1}^2-a_{n+2}a_n={(-1)}^n{}$ が成り立つ.
山口大学(2022年/(教育)第3問)
次の条件によって定まる数列 $\left\{a_n\right\}$ がある。
$a_1=1$、$a_2=1$、$a_{n+2}=a_{n+1}+a_n$ $(n=1,2,3, \cdots)$
次の問いに答えなさい。
(1)漸化式 $a_{n+2}=a_{n+1}+a_n$ を $a_{n+2}-\alpha a_{n+1}=\beta\left(a_{n+1}-\alpha a_n\right)$ と変形したとき、定数 $\alpha$ と $\beta$ の値を求めなさい。ただし、$\alpha<\beta$ とする。
(2)$b_n=a_{n+1}-\alpha a_n$ $(n=1,2,3, \cdots)$ とおく。数列 $\left\{b_n\right\}$ の初項 $b_1$ と一般項 $b_n$ を求めなさい。
(3)数列 $\left\{a_n\right\}$ の一般項 $a_n$ を求めなさい。
《コメント》
フィボナッチ数列の特徴を捉える上で欠かすことのできない「リュカ数列」に関する問題も蒐集しています。リュカ数列とは、フィボナッチ数列と同じ漸化式を満たし、初項が $a_1=1$、$a_2=3$ であるような数列です。フィボナッチ数列とリュカ数列の間には興味深い関係式が数え切れないほど存在します。
