問題1.2.1
行列の計算を行え。
(1)$\left[\begin{array}{rrr}2 & -1 & 2 \\ 1 & 5 & -2\end{array}\right]\left[\begin{array}{rrr}2 & 3 & -2 \\ 0 & -2 & 7 \\ 1 & 1 & 3\end{array}\right]$
(2)$\left[\begin{array}{r}2 \\ -1 \\ 4\end{array}\right]\left[\begin{array}{lll}3 & 1 & -2\end{array}\right]$
(3)$\left[\begin{array}{lll}3 & 1 & -2\end{array}\right]\left[\begin{array}{r}2 \\ -1 \\ 4\end{array}\right]$
(4)$\left[\begin{array}{lll}0 & 1 & 2 \\ 0 & 0 & 1 \\ 0 & 0 & 0\end{array}\right]^{3}$
(5)$\left[\begin{array}{rrr}2 & 3 & -1 \\ 0 & 5 & 4 \\ -1 & 0 & -2\end{array}\right]\left\{\left[\begin{array}{rrr}0 & 5 & 9 \\ 3 & -2 & 8 \\ -1 & 8 & 1\end{array}\right]-2\left[\begin{array}{rrr}-1 & 0 & 1 \\ 3 & 2 & 3 \\ -4 & 2 & -1\end{array}\right]\right\}$
ポイント
行列の演算で困るとすれば、行列同士の積(Matrix Multiplication)でしょうか。行列の乗算は次のようなイメージで行うと明快です。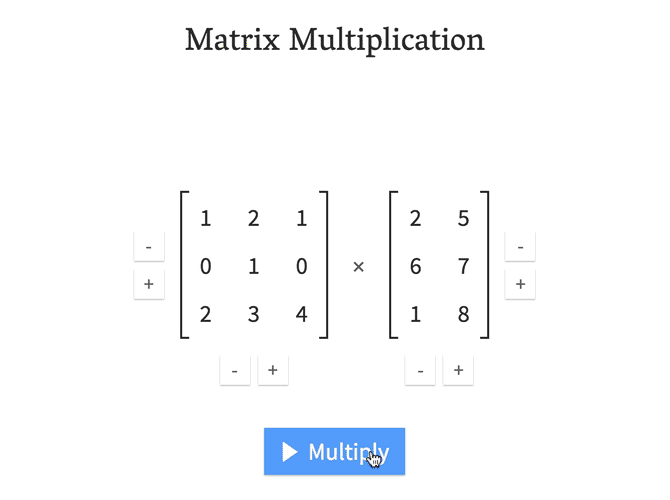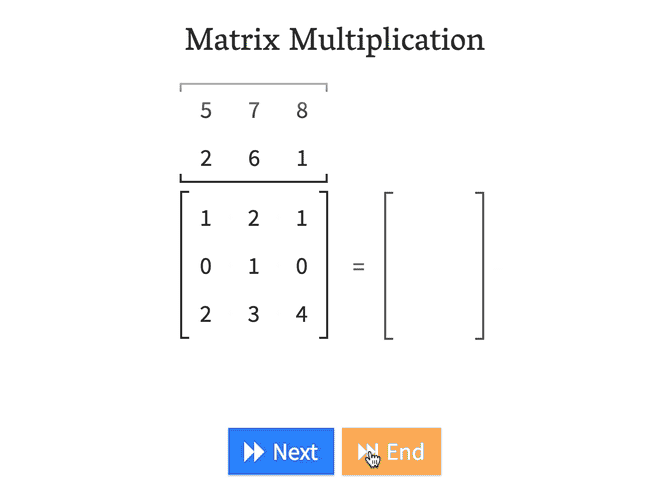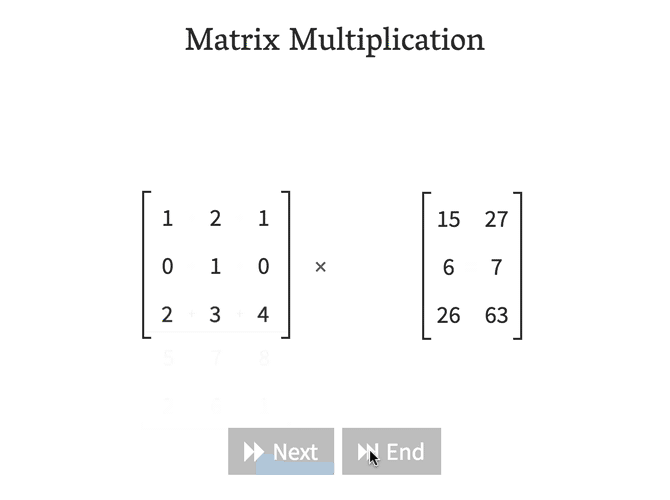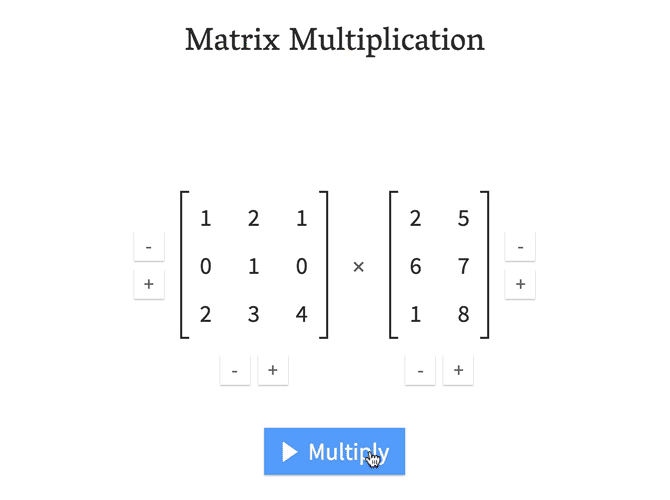
解答例
(1)$$\left[\begin{array}{ccc}2 & -1 & 2 \\ 1 & 5 & -2\end{array}\right]\left[\begin{array}{ccc}2 & 3 & -2 \\ 0 & -2 & 7 \\ 1 & 1 & 3\end{array}\right]=\color{red}{\left[\begin{array}{ccc}6 & 10 & -5 \\ 0 & -9 & 27\end{array}\right]}$$
(2)$$\left[\begin{array}{c}2 \\ -1 \\ 4\end{array}\right]\left[\begin{array}{ccc}3 & 1 & -2\end{array}\right]=\color{red}{\left[\begin{array}{ccc}6 & 2 & -4 \\ -3 & -1 & 2 \\ 12 & 4 & -8\end{array}\right]}$$
(3)$$\left[\begin{array}{ccc}3 & 1 & -2\end{array}\right]\left[\begin{array}{c}2 \\ -1 \\ 4\end{array}\right]=\color{red}{-3}$$
(4)$$\begin{align}{\left[\begin{array}{ccc}0 & 1 & 2 \\ 0 & 0 & 1 \\ 0 & 0 & 0\end{array}\right]^{3}} & =\left[\begin{array}{ccc}0 & 1 & 2\\ 0 & 0 & 1 \\ 0 & 0 & 0\end{array}\right]\left[\begin{array}{ccc}0 & 0 & 1\\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right] \\ \\ & =\color{red}{O}\end{align}$$
(5)$$\begin{align}
&\ \ \ \ \ \left[\begin{array}{ccc}
2 & 3 & -1 \\
0 & 5 & 4 \\
-1 & 0 & -2
\end{array}\right]\left\{\left[\begin{array}{ccc}
0 & 5 & 9 \\
3 & -2 & 8 \\
-1 & 8 & 1
\end{array}\right]-2\left[\begin{array}{ccc}
-1 & 0 & 1 \\
3 & 2 & 3 \\
-4 & 2 & -1
\end{array}\right]\right\} \\
&={\left[\begin{array}{ccc}
2 & 3 & -1 \\
0 & 5 & 4 \\
-1 & 0 & -2
\end{array}\right]\left[\begin{array}{ccc}
2 & 5 & 7 \\
-3 & -6 & 2 \\
7 & 4 & 3
\end{array}\right]} \\
&=\color{red}{\left[\begin{array}{ccc}
-12 & -12 & 17 \\
13 & -14 & 22 \\
-16 & -13 & -13
\end{array}\right]}
\end{align}$$
