ベンゼン分子の振動モード(vibrational modes of the benzene molecule)全30種を動画付きで一覧にしました!
振動モードについて
まずは振動モードについておさらいしておきましょう。
分子の運動には、
・重心が移動する並進運動
・重心の周りの回転運動
・原子間距離が伸び縮みする振動運動
の3種類が存在します。$N$個の原子から成る分子($N$原子分子)が3次元空間を自由に移動できる時、その分子の自由度は $3N$ となります。つまり各原子の $x$座標、$y$座標、$z$座標を定めることで、分子の3次元的な位置関係を記述することができます。
ただし、それぞれの原子は全く独立に動き回れるわけではなく、分子として一体となって存在しているため、分子の自由度の一部はこの制約に割かれます。3次元方向の並進の自由度は$3$であり、重心の周りの回転運動の自由度は、直線分子では$2$、非直線分子では$3$となります。従って、振動の自由度は全体の自由度 $3N$ から並進と回転の自由度を差し引いた $3N-5$ もしくは $3N-6$ となります。各分子にはちょうどこの数に対応する分の振動モードが存在しています。
例えば、$\mathrm{H_2 O}$は$3$原子からなる非直線型の分子なので、$3 \times 3-6$、すなわち$3$つの振動モードが存在します。また $\mathrm{CO_2}$は$3$原子からなる直線型の分子なので$4$つの振動モードを持つことがわかります。
ベンゼンの振動モード
ベンゼンは$12$原子からなる非直線型の分子なので、振動モードは$$3 \times 12-6=30\,\text{個}$$だけ存在します。化学系の大学院入試にも時々出題されることがあります。
以下にベンゼンの全30種の振動モードの振動数を掲載します。振動数計算はGaussian16プログラムを用い、ωB97X-D/def2TZVPPレベルで行いました。なお、以下に示す振動数はスケーリング*1していないので注意して下さい。
| 振動モード一覧表 | |
| No. | ($\mathrm{cm}^{-1}$) |
| 振動モード1 | 417.30 |
| 振動モード2 | 417.32 |
| 振動モード3 | 627.09 |
| 振動モード4 | 627.37 |
| 振動モード5 | 699.81 |
| 振動モード6 | 732.94 |
| 振動モード7 | 882.34 |
| 振動モード8 | 882.99 |
| 振動モード9 | 1013.08 |
| 振動モード10 | 1013.76 |
| 振動モード11 | 1029.86 |
| 振動モード12 | 1032.35 |
| 振動モード13 | 1039.30 |
| 振動モード14 | 1073.65 |
| 振動モード15 | 1073.87 |
| 振動モード16 | 1179.53 |
| 振動モード17 | 1209.18 |
| 振動モード18 | 1209.74 |
| 振動モード19 | 1340.07 |
| 振動モード20 | 1390.05 |
| 振動モード21 | 1530.21 |
| 振動モード22 | 1530.36 |
| 振動モード23 | 1669.64 |
| 振動モード24 | 1669.96 |
| 振動モード25 | 3187.51 |
| 振動モード26 | 3197.34 |
| 振動モード27 | 3197.63 |
| 振動モード28 | 3213.51 |
| 振動モード29 | 3213.82 |
| 振動モード30 | 3224.07 |
ベンゼンの振動モード
以下にベンゼンの振動モード全30種のgif画像を低波数側から掲載します。括弧内の数値は振動数(計算値)です。
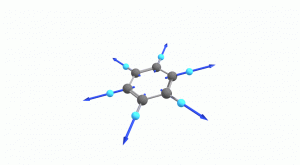
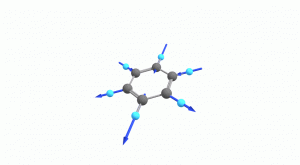
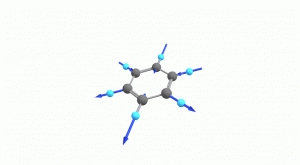
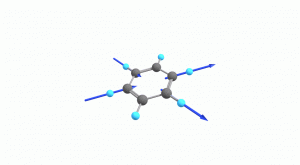
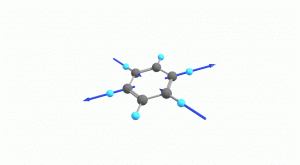
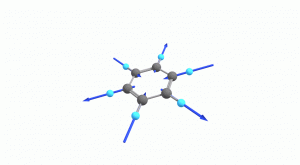
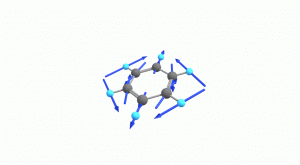
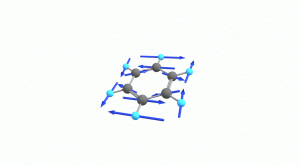
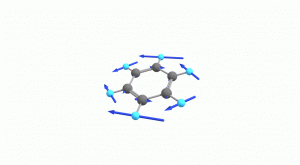

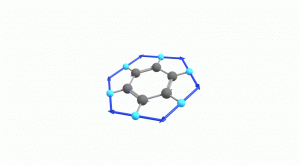
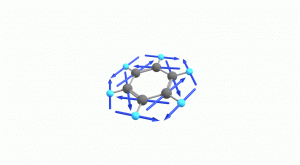
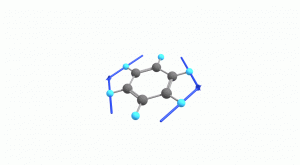
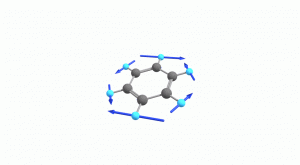
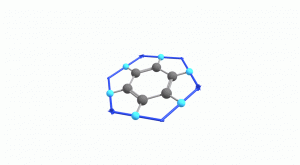
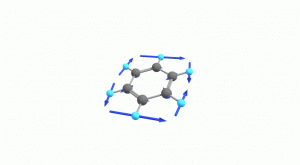
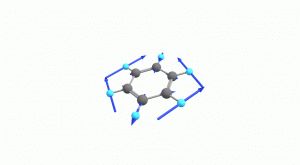
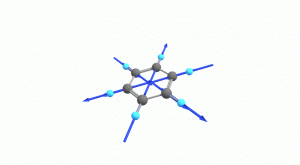
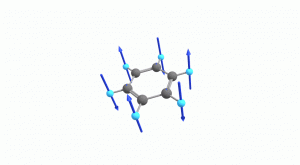
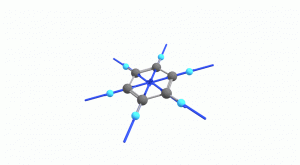
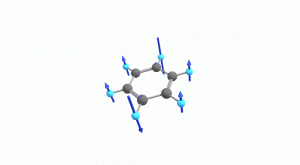
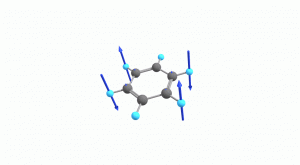
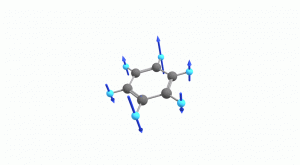
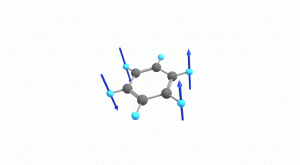
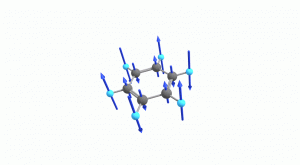
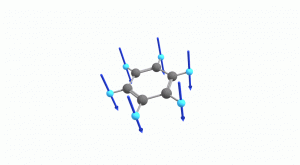
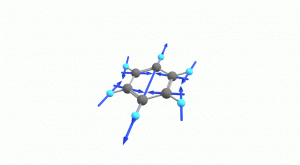
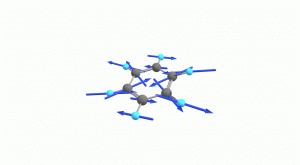
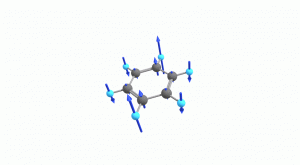
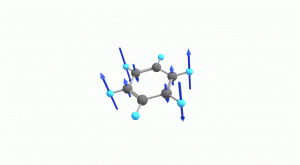
以上の30種がベンゼンの振動モードです。計算上では30個の振動モードがあると言われても、実際に見てみないことにはなかなかイメージがつかないと思います。振動モードについて、少しでも具体的なイメージを掴んで貰えれば幸いです。
*1 ポテンシャルエネルギー面の非調和性を考慮する必要がありますが、これを考慮して計算するのは一般に高コストです。そこで、計算を省力化するために調和関数(二次関数)でポテンシャル面を近似する「調和振動子近似」が用いられます。この近似による誤差は数%程度であり、スケールファクターを用いて実測値に合うように補正することができます。アメリカ国立標準技術研究所のページに計算値のスケーリング係数の一覧表が掲載されています。この表によれば、例えばωB97X-D/def2TZVPPの場合は係数が0.955とされています。非調和性を考慮していない振動数計算では一般に振動数が大きめの値として得られることから、ほとんどの係数は$1$より小さい値となります。
一般的なポテンシャル面は二次曲線ではなく、結合は引き延ばされ続けるといずれは開裂します。調和振動子近似に基づく結合は実際よりも剛直に評価されてしまうため、振動数が大きめに見積もられることになります。
