メタンの水素原子は区別できるのか

「はみ出し高校化学シリーズ」と題して教科書には載っていないであろう余計な豆知識をご紹介していきます。本企画の第1弾として、皆さんよくご存知のメタン分子CH₄を取り上げます。

 

 メタン分子

メタン（分子式：$\mathrm{CH_4}$）は最も基本的な有機化合物であり、最も単純なアルカンの一つです。

以下に立体構造を示します（3Dモデルは自由に動かせます）。

メタン分子 $\mathrm{CH_4}$ の$\text{C-H}$結合はいずれも正四面体方向に伸びており、水素原子はいずれも等価です（※注）。そのため、残念ながらメタンの４つの水素原子を実験的に区別することは不可能です。

 

 同位体を含む場合

早々に結論が出てしまいましたが、水素の同位体である重水素（デューテリウム (英: deuterium)）を含む場合はどうでしょう？

例えば、singly deuterated methane（4個の水素のうち1個だけを重水素 $\mathrm{D}$ に置換したメタン $\mathrm{CDH_3}$ ）の場合、振動の角運動量や回転のモーメントが異なるので、普通のメタンとは区別することが可能です。しかし、相変わらず残りの３つの水素原子は区別することができません。

 

 どういうときに水素原子が区別できるのか

世の中の水素原子（もちろん他の元素についても）には名前や番号がついてる訳ではありません。水分子から引きちぎって得られる水素も、メタンから引きちぎって得られる水素も、どちらも同じ水素原子であり区別することができません。

水素原子を区別することができるのは、水素原子が置かれた「環境」が異なる場合に限ります。

---

例えば、プロピオン酸 $\mathrm{C_{2}H_{5}COOH}$ に含まれる水素原子は計６個ですが、このうち区別できるのは３種類です。

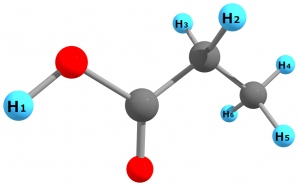
６個の水素原子はそれぞれ、

①カルボキシル基の水素（$\mathrm{H_{1}}$）
②メチレン基の水素（$\mathrm{H_{2}}$と$\mathrm{H_{3}}$）
③メチル基の水素（$\mathrm{H_{4}}$～$\mathrm{H_{6}}$）

の3種類に分類できます。②の水素原子は左右で区別できそうですが、$\text{C-C}$単結合は自由に回転可能なので$\mathrm{H_{2}}$と$\mathrm{H_{3}}$は区別できません。

このことは「プロピオン酸には環境の異なる３種類の水素原子が存在する」と言い換えることができます。

メタン分子内の水素原子の環境は１種類しかなので互いに区別することができません。同じように、ベンゼンの水素原子も１種類の環境しかないので区別できません。

 

 メタンの水素原子を無理やり交換してみる

実験的にはもちろん水素を区別することはできません。しかし、コンピューター上では水素に番号を振って区別することができます。

化学の世界には計算化学という分野があり、電子の状態や結合の様子などをコンピューターを用いた計算（より正確には「量子化学計算」）によって再現して解析することができます。そこで、この計算化学の知識を用いて、メタンの水素原子を交換するのに必要なエネルギーを見積もってみました。

下図に固有反応座標（IRC）に沿ったエネルギープロファイルを示します。横軸は反応座標、縦軸は電子エネルギー（単位は kJ/mol ）です。

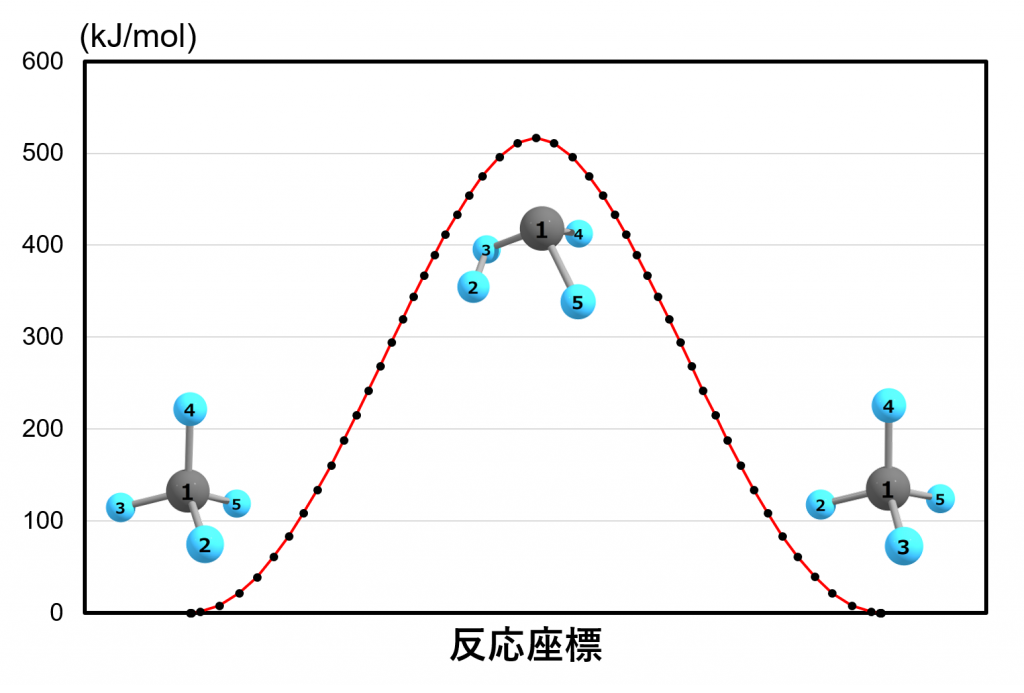
左側の構造では2という番号のついた水素が手前にありますが、右側の構造では3という番号のついた水素が手前に来ています。真ん中の構造はエネルギーが最も高くなる遷移状態に相当します。およそ 500 kJ/mol 程度の活性化エネルギーが必要であることが分かります。

実験的に知られている炭素-水素結合の結合エネルギーはおよそ 413 kJ/mol なので、$\text{C-H}$結合を2本分引きちぎっている割には活性化障壁が低いみたいですね。

---