本稿では前回の内容を踏まえ、ファンデルワールスの状態方程式に数学的処理を施し、変曲点の謎を明らかにしていく。
-
状態方程式と等温線
さて、前項では気体の状態方程式の有用性を理解した。ここからはファンデルワールスの状態方程式によって得られる等温線について考察する。
そもそも等温線というのは温度を一定としたときの圧力と体積の相関関係を表す曲線のことで、等温線上の点に相当する全ての系は互いに熱平衡にある。アイルランドの化学者・物理学者であったトーマス・アンドリューズ(Thomas Andrews:1813~1885)は1863年頃、二酸化炭素の気体を様々な温度において圧縮する実験を行い、ある温度以上ではどんなに圧力を高めても気体が液化しないことを発見した。彼はこの温度を「臨界温度」と呼び、更に臨界温度下、ある圧力では気体と液体の区別が付かなくなる現象が起きることを発見した。このような点を「臨界点」(critical point)と名付け、物質固有の点であることを明らかにした。(以上の内容は1869年の論文The Bakerian Lecture “On the Continuity of the Gaseous and Liquid States of Matter”に基づく。これはネット上に公開されている論文であるので興味のある方は参照して頂きたい)
実験の過程で様々な等温線を得ることに成功したアンドリューズは、論文の中で相に関する事実にも言及している。等温線の圧力-体積相関図において、ある温度以下であれば傾きが$0$となる区間が現れるが、この区間では気液平衡にある。これより高い温度から低い温度へと温度を下げていったとき、初めて傾きが$0$となる区間が現れてくる温度が臨界温度であることを実験的に証明したのである。これは図で見た方が分かりやすいかもしれない。
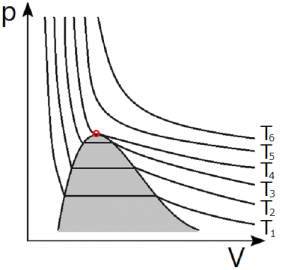
上図は様々な温度($T_1<T_2<\cdots<T_6$)における等温線の圧力-体積相関図(概略)であり、灰色の網掛け部分は気液平衡が成立する領域を表している。
比較的高温($T_5$、$T_6$)では等温線が双曲線に近く、比較的低温($T_1$~$T_3$)では灰色の領域で傾きが$0$となる。ある温度以上ではいかなる圧力下でも気体が液化しない、というのが臨界温度の定義であったから、ちょうど灰色領域に等温線が接する温度$T_4$がこの図で言うところの臨界温度に相当し、灰色領域と等温線の接点(赤丸で示した)が臨界点を表している。赤丸で示した点は実は変曲点となっており、更に傾きが$0$である。問題演習などでは天下り的に「変曲点で傾き$0$⇒臨界点」と与えられてしまうのだが、これでは非常に味気無い。上記のような事情を踏まえれば「変曲点で傾き$0$⇒臨界点」という理屈が納得できるはずである。
※ここで注意して欲しいのが、灰色で図示された領域における状態方程式が実際に直線になっている訳ではない、ということである。灰色領域内の曲線部は「ファンデルワールスのループ」と呼ばれ物理的な意味を持たない。そこで「マクスウェルの構成法」という方法で実験結果に即する形に直線化する。この数学的手続きを済ませた図が上記の図である。詳しい解説は参考書に委ねることにする。
-
解析的数学による理解
ここでもう一度ファンデルワールスの状態方程式を見てみよう。$$p=\dfrac{RT}{V_m-b}-\dfrac{a}{V_m^2} \tag{1.4.2}$$ $(1.4.2)$式は$V_m$の関数と見なすことができ、温度$T$を定数として圧力$p$の導関数を導くことができる。このとき見通し良く計算するために$(1.4.2)$式を$$p=RT(V_m-b)^{-1}-a V_m^{-2} \tag{1.4.3}$$と書くと良い。これより、$$\begin{cases} \left(\dfrac{\partial p}{\partial V_m}\right)_T=-RT(V_m-b)^{-2}+2a V_m^{-3} \\ \left(\dfrac{{\partial}^2 p}{\partial V_m^2}\right)_T=2RT(V_m-b)^{-3}-6a V_m^{-4} \end{cases}$$を得る。$(1.4.3)$式は2変数関数であるから、実際には「圧力$p$の偏導関数」となっていることに注意して欲しい。さて、この2式より「変曲点で傾き$0$」という条件を数式化することができる。つまり、
$\left(\dfrac{\partial p}{\partial V_m}\right)_T=0$ かつ $\left(\dfrac{{\partial}^2 p}{\partial V_m^2}\right)_T=0$
がファンデルワールスの状態方程式に基づく臨界点を与える条件であり、$$\begin{cases} -RT(V_m-b)^{-2}+2a V_m^{-3}=0 \\ 2RT(V_m-b)^{-3}-6a V_m^{-4}=0\end{cases}$$となる。計算の方法は幾つか考えられるが、そのうち最も簡単だと思われるものを紹介しよう。上記の2式は$$\begin{cases} RT(V_m-b)^{-2}=2a V_m^{-3} \ \cdots ① \\ RT(V_m-b)^{-3}=3a V_m^{-4} \ \cdots ②\end{cases}$$と変形できる。①の辺々を②の辺々で割って、$$V_m-b=\dfrac{2}{3}V_m$$ $$\therefore V_m=3b$$を得る。これを①に代入すると$$\dfrac{RT}{(2b)^2}=\dfrac{2a}{(3b)^3}$$ $$\therefore T=\dfrac{8a}{27Rb}$$を得る。これらの値を$(1.4.2)$式に代入して$$p=\dfrac{a}{27b^2}$$を得る。以上より、臨界点における圧力$p_c$、体積$V_c$、温度$T_c$の値はそれぞれ$$\begin{cases} p_c=\dfrac{a}{27b^2} \\ V_c=3b \\ T_c=\dfrac{8a}{27Rb} \end{cases}$$となる(添え字の$c$は臨界点 “critical point” の意)。これらの値をまとめて臨界定数などと呼ぶことがある。これらの値は覚えるようなものではなく、導出の方法を知っておくことが最も重要である(学生相手の学部の試験などでは、大抵こうした導出方法が問われるのである)。
-
代数的な臨界定数の導出
臨界定数を導出する方法は他にも存在する。例として$(1.4.2)$式を$V_m$の多項式と見なす方法を紹介しておく。$(1.4.2)$式を変形すると$$V_m^3-\left(b+\dfrac{RT}{p}\right)V_m^2+\dfrac{a}{p}V_m-\dfrac{ab}{p}=0$$となる。この$V_m$の3次式が「変曲点(臨界点)で傾き$0$」という条件を満たすとき、数学で言うところの「因数定理」により$$(V_m-V_c)^3=0$$が成立する。これを展開すると$$V_m^3-3V_c V_m^2+3V_c^2 V_m-V_c^3=0$$となるから上式と係数を比較すると$$\begin{cases} 3V_c=b+\dfrac{RT_c}{p_c} \\ 3V_c^2=\dfrac{a}{p} \\ V_c^3=\dfrac{ab}{p} \end{cases}$$となる。これらより各定数を求めることができる。
-
実在気体へ
またこれらの臨界定数により、臨界圧縮因子 $Z_c=\dfrac{p_cV_c}{RT_c}$ は$$Z_c=\dfrac{3}{8}=0.375$$で与えられることが分かる。実在気体ではこれよりやや小さい値となるのだが、気体について統一的な理解が可能となったことは物理化学上の大きな進歩であった。
以上の数学的操作はファンデルワールスの状態方程式のみならず、ベルテロ―(仏1827~1907)やディーテリチ(独1858~1929)の状態方程式にも適用可能である。
※ディーテリチ(Dieterici)の状態方程式は$$p=\dfrac{RT}{V_m-b}e^{-a/RTV_m}$$で与えられ、これによれば$$\begin{cases} p_c=\dfrac{a}{4e^2 b^2} \\ V_c=2b \\ T_c=\dfrac{a}{4Rb} \end{cases}$$となり、臨界圧縮因子は$$Z_c=\dfrac{2}{e^2}=0.27067…$$で与えられる。この値はファンデルワールスの状態方程式により与えられる臨界圧縮因子の値より小さく、非極性分子の実測値の良い近似値となる。
ここまで見てきたように実在気体には幾つかの因子によるパラメータが存在し、パラメータによる効果を表す補正項を導入することでより一般的な考察が可能となった。これは理論化学における、まさに「科学的」な進展であったと言えよう。
参考文献:
・アトキンス 物理化学(上)第8版(第1章~)
東京化学同人/第8刷(2015)
・マッカーリ/サイモン 物理化学(下)第1版(第16章~)
東京化学同人/第9刷(2013)
・化学・生命科学系のための物理化学 第1版(第2章~)
東京化学同人/第4刷(2008)