ここ最近まではワールドカップのせいで寝不足、という方が多かったのではないでしょうか。管理人はワールドカップが有ろうが無かろうがいつも寝不足です(笑)。
創作整数問題#42
《問題#42》
自然数$k$、$n$を用いて $\sqrt{n^k+1}+\sqrt{n^k-1}$ と表せるような有理数は存在しないことを示せ。
(創作問題)
よくある問題のちょっとした一般化です。
証明問題につき、解答は次回掲載。
創作整数問題#41(解き方)
| 整数$x$、$y$に対して、連立方程式$$\begin{cases}y = 3x^3 + 9x^2 + 9x + 2 \\ x = 3y^3 + 9y^2 + 9y + 2\end{cases}$$の解をすべて求めよ。 |
|---|
各式の両辺に$1$を加えて整理すると$$\begin{cases}y+1 = 3(x+1)^3 \\ x+1 = 3(y+1)^3 \end{cases}$$を得ます。これより$y$を消去して、$$x+1=81(x+1)^9$$ $$\therefore (x+1)\left\{81(x+1)^8-1\right\}=0$$となります。どのような整数$x$に対しても $81(x+1)^8$ が$1$となることはないから、これを満たす整数$x$は$$x=-1$$に限られます。よって $y=-1$ を得るので、求める組は$$(x,y)=\color{red}{(-1,-1)}$$のみであることが分かります。
両辺に$1$を足すという操作を思い付かないと、$y$をそのまま代入して$$x=3(3x^3+9x^2+9x+2)^3 \\ \ \ \ \ \ \ \ \ +9(3x^3+9x^2+9x+2)^2 \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +9(3x^3+9x^2+9x+2)+2$$という方程式を解かなければいけません(一応解けないことはないですが、これを解ける人は最初から両辺に$1$を足せると思います・・・)。
両辺に$1$を足す方法以外にも、連立方程式が$x$、$y$について対称であることを利用すれば次のような別解も考えられます。
《別解》
各式の両辺を辺々加えて、$$(x+y)=3(x^3+y^3)+9(x^2+y^2)+9(x+y)+4$$を得る。ここで$$\begin{cases}x+y = p \\ xy = q \end{cases}$$と置く($p$、$q$は整数であることに注意)と、$$p=3(p^3-3pq)+9(p^2-2q)+9p+4$$ $$\therefore 3p^3+9p^2+(8-9q)p-18q+4=0$$となり、これより$$9(p+2)q=3p^3+9p^2+8p+4$$と変形できる。$p \ne -2$ のとき$$q=\dfrac{3p^2+3p+2}{9}$$を得るが、$q$は整数なので $3p^2+3p+2$ が$9$の倍数となることが必要である。しかしどのような整数$p$に対しても $3p^2+3p+2$ は$3$で割った余りが$2$となり、$9$の倍数にならないから不合理である。故に与方程式が整数解をもつならば $p=-2$ の場合に限る。これより $y=-x-2$ となるから代入して、$$x = 3(-x-2)^3 + 9(-x-2)^2 + 9(-x-2) + 2$$ $$\therefore x=-3x^3-9x^2-9x-4$$ $$\therefore 3x^3+9x^2+10x+4=0$$ $$\therefore (x+1)(3x^2+6x+4)=0$$を得る。$3x^2+6x+4 \geqq 3(x+1)^2+1$ より、$$\therefore x=-1$$よって求める組は$$(x,y)=\color{red}{(-1,-1)}$$となる。
(コメント)
連立されている2式が$x$、$y$について対称であるということは、座標平面上において2曲線が直線 $y=x$ に関して対称であることを意味します。したがって$(a,b)$が解のとき$(b,a)$もまた解となります。因みに本問の2曲線$$\begin{cases}\color{blue}{y = 3x^3 + 9x^2 + 9x + 2} \\ \color{red}{x = 3y^3 + 9y^2 + 9y + 2} \end{cases}$$を$xy$平面上にプロットすると以下のようになります。
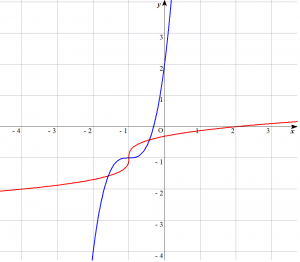
交点は全部で3点存在し、$\left(-\dfrac{3+\sqrt{3}}{3},-\dfrac{3+\sqrt{3}}{3}\right)$、$(-1,-1)$、$\left(-\dfrac{3-\sqrt{3}}{3},-\dfrac{3-\sqrt{3}}{3}\right)$となります。
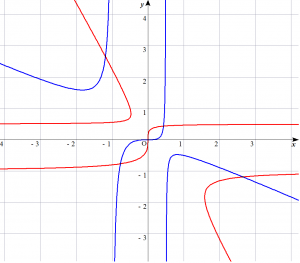
この図だけを見たら $y=x$ のときしか解が存在しないように思われるかもしれませんが、曲線が複雑なときはその限りではありません。例えば$$\begin{cases}\color{blue}{y = x^3+2x^2 y+xy} \\ \color{red}{x = y^3+2x y^2 +xy} \end{cases}$$のとき、連立方程式は$x$、$y$について対称ですが、$xy$平面上にプロットすると以下のようになり、必ずしも直線 $y=x$ 上で交点をもつわけではないことが分かります。