今回は名古屋大学のシンプルな整数問題から。
《問題》
正の整数$n$の正の平方根 $\sqrt{n}$ は整数ではなく、それを$10$進法で表すと、小数第$1$位は$0$であり、第$2$位は$0$以外の数であるとする。
(1)このような$n$の中で最小のものを求めよ。
(2)このような$n$を小さいものから順に並べたときに$10$番目にくるものを求めよ。
(名古屋大学2019年 前期理系第3問)
《考え方》
題意を掴むのは容易ですが、実際に例を挙げるとなると少し難しいかもしれません。
「$10$進法で表すと、小数第$1$位は$0$であり、第$2$位は$0$以外の数である」というのは例えば、$$1.0488…$$などが該当します。$\sqrt{n}$が整数でないので、$n$は平方数でないことが分かります。このような$n$について、$\sqrt{n}$が$$m.0xyz…$$という形で表せるものを探します。そのような条件の言い換えとなる不等式をうまく立式しましょう。
● ● ●
解答例
(1)
$\sqrt{n}$を超えない最大の整数を$m$とすると、$\sqrt{n}$が整数でないことから$$(0<)\,m<\sqrt{n}<m+1$$が成り立つ。この各辺を二乗して$$m^2<n<m^2+2m+1$$を得るので、整数$n$はある正の整数$k$を用いて$$n=m^2+k$$と置ける。ただし$k$は $1 \leqq k \leqq 2m$ を満たす。
$k=1$ のとき、$\sqrt{n}$、すなわち $\sqrt{\mathstrut m^2+1}$ の小数第$1$位が$0$であり、小数第$2$位が$0$以外の数となる条件は$$m+\dfrac{1}{100}\leqq \sqrt{\mathstrut m^2+1} < m+\dfrac{1}{10}$$となる。右側の不等式について、両辺正より平方して整理すると$$m>\dfrac{99}{20}$$となる。そこで $m=5$ とすると $n=26$ であり、$$5.01^2(=25.1001)<26<5.1^2(=26.01)$$より、$\sqrt{26}$は確かに小数第$1$位が$0$であり、小数第$2$位が$0$以外の数となっている。
したがって求める最小の$n$は$$n=\color{red}{26}$$である。
(2)
不等式$$m+\dfrac{1}{100}\leqq \sqrt{\mathstrut m^2+1} < m+\dfrac{1}{10}$$を$m$について解いて$$\dfrac{99}{20}<m \leqq \dfrac{9999}{200}$$を得る。これを満たす整数$m$は$$m=5,6,\cdots,49$$である。
次に $k=2$ のとき、$\sqrt{n}$、すなわち $\sqrt{\mathstrut m^2+2}$ の小数第$1$位が$0$であり小数第$2$位が$0$以外の数となる条件は$$m+\dfrac{1}{100}\leqq \sqrt{\mathstrut m^2+2} < m+\dfrac{1}{10}$$となるから、これを$m$について解いて$$\dfrac{199}{20}<m \leqq \dfrac{19999}{200}$$を得る。これを満たす整数$m$は$$m=10,11,\cdots,99$$である。
$k \geqq 3$ のとき、必要条件となる不等式$$m+\dfrac{1}{100}\leqq \sqrt{\mathstrut m^2+k} < m+\dfrac{1}{10}$$の右側の不等式について、解となる$m$の範囲を求めると$$m>5k-\dfrac{1}{20}$$となる。$k \geqq 3$ より、少なくとも $m>14$ となるから$10$番目の$n$を求める際に考慮する必要はない。
以上より、題意を満たす整数$n$を小さい順に$10$個だけ列挙すると
$5^2+1$, $6^2+1$, $7^2+1$, $8^2+1$, $9^2+1$, $10^2+1$, $10^2+2$, $11^2+1$, $11^2+2$, $12^2+1$
となる。
以上より、求める$10$番目の$n$の値は$$\color{red}{145}$$である。
(コメント)
本問は不等式の作り方がポイントとなります。$\sqrt{n}$の小数部分について議論したいので、これを超えない最大の整数を文字で置くと見通しが良くなります(解答例では$m$と置いています)。
(1)ではいきなり $k=1$ としていますが、不等式を満たす$n$のうち、できるだけ小さいものを見つけたいので、まず $n=m^2+1$ のケースを考えています。(1)で題意を満たす$n$がどのように構成できるのかを調べられたので、(2)では $n=m^2+2$ や $n=m^2+3$ などの場合も考えることになります。
要するに、曲線 $y=\sqrt{x}$ 上の点で、$x$は整数であるが$y$は整数にならないもののうち、領域$$\dfrac{1}{100} \leqq y-[\sqrt{x}\,] \leqq \dfrac{1}{10}$$内に存在するものを見つけよ、というのが本問の本質的な部分です($[\sqrt{x}\,]$はガウス記号)。以下に座標平面上に表したときの図を示します。
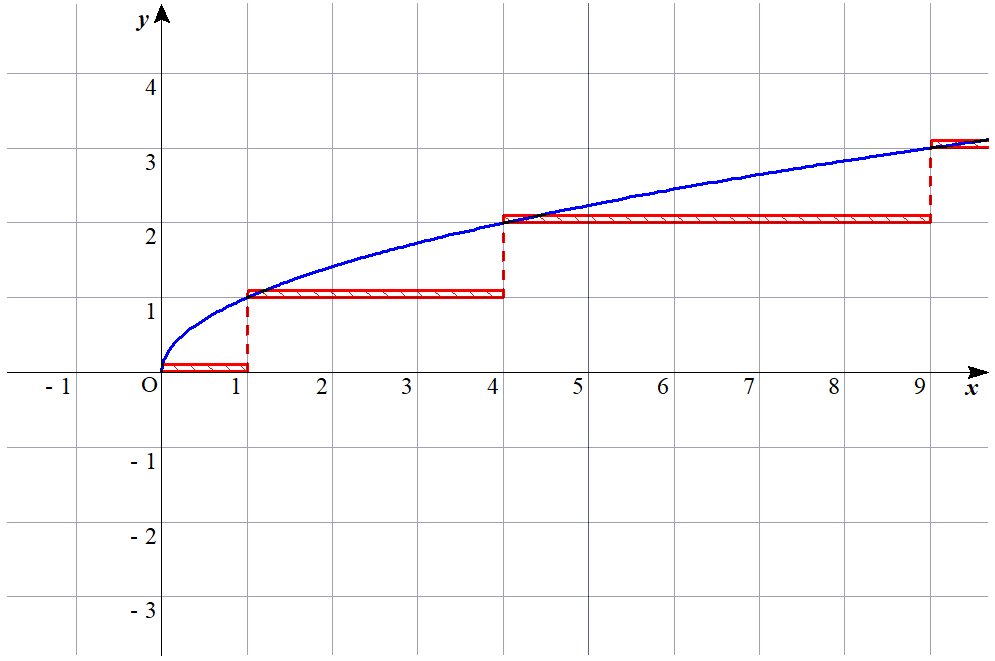
$x=26$ のときに初めて赤色斜線部の領域に点$(26,\sqrt{26})$が乗ります(因みに、$\sqrt{26}=5.099…$ です)。この図から、$x$が大きくなって $y=\sqrt{x}$ の増え方がなだらかになるにしたがって赤色部分に含まれる点が増えることが直感的に理解できると思います。
● ● ●
本問は次のように一般化できそうです。
《おまけ問題》
$k$を正の整数とする。正の整数$n$の正の平方根 $\sqrt{n}$ は整数ではなく、それを$10$進法で表すと、小数第 $k$ 位までの数字はすべて$0$であり、第 $k+1$ 位の数字は$0$以外の数であるとする。このような$n$の中で最小のものを求めよ。
考えるべき不等式はほとんど変わりませんね!
なお、本問の類題が2016年の東大理科前期第5問に出題されています。
(2019/12/10 追記)
本問の類題(それより高級?)が今年、2019年の1月に開催された第37回北海道高等学校数学コンテストに出題されています。講評を拝見した限りでは、あまり芳しい出来ではなかったようですが、このテーマはたまに入試の現場で登場することがあるので、考え方には慣れておきたいものだなと改めて感じました。
