本稿では東京大学の理系数学第3問を取り上げます。シンプルな図形の問題でした。場合分けが発生することを見落とさなければ完答できるかと思います。
平行四辺形 $ ABCD $ において,$ \angle ABC = \dfrac{\pi}{6} $, $ AB = a $, $ BC = b $, $ a \leq b $ とする。次の条件を満たす長方形 $ EFGH $ を考え,その面積を $ S $ とする。
条件:点 $ A, B, C, D $ はそれぞれ辺 $ EF, FG, GH, HE $ 上にある。
ただし,辺はその両端の点も含むものとする。
(1)$ \angle BCG = \theta $ とするとき,$ S $ を $ a, b, \theta $ を用いて表せ。
(2)$ S $ のとりうる値の最大値を $ a, b $ を用いて表せ。
(2025年 東京大学 理科前期第3問)
図形の位置関係は下図のようになる。
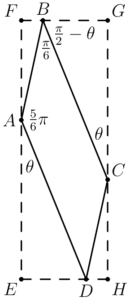
(1)
\[\begin{aligned} S &= 2 \triangle ABF + 2 \triangle BCG + 2 \triangle ABC \\ &= 2 \cdot \frac{1}{2} \left\{ a \cos \left( \frac{\pi}{6}-\theta \right) \right\} \cdot a \sin \left( \frac{\pi}{6}-\theta \right) \\ & \quad + 2 \cdot \frac{1}{2} \cdot (b \cos \theta) \cdot b \sin \theta + 2 \cdot \frac{1}{2} ab \sin \frac{\pi}{6} \\ &= \frac{a^2}{2} \sin \left( \frac{\pi}{3}-2\theta \right) + \frac{b^2}{2} \sin 2\theta + \frac{ab}{2}\\ &= \boxed{\frac{2b^2-a^2}{4} \sin 2\theta + \frac{\sqrt{3}}{4} a^2 \cos 2\theta + \frac{ab}{2}} \end{aligned} \]
長方形 $EFGH$ の頂点を,
\[E = (0,d),\quad F = (L,d),\quad G = (L,0),\quad H = (0,0)\]と置く.このとき長方形の面積は $S = Ld$ である.
内接する平行四辺形 $ABCD$ の各頂点は,それぞれ次のように取る.
\[A = (p,d) \quad (A\in EF),\quad B = (L,d-q) \quad (B\in FG),\]
\[C = (L-p,0) \quad (C\in GH),\quad D = (0,q) \quad (D\in HE),\]ただし $0\le p\le L$, $0\le q\le d$ であり,平行四辺形であるため
\[\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\]が成立する.
(A)辺 $AB$ の長さが $a$ であることより,
\[\small AB = \sqrt{(L-p)^2 + [d-(d-q)]^2} = \sqrt{(L-p)^2+q^2} = a.\]故に
\[(L-p)^2 + q^2 = a^2. \tag{1}\]
(B)辺 $BC$ の長さが $b$ であることより,
\[\small BC = \sqrt{[(L-p)-L]^2 + [0-(d-q)]^2} = \sqrt{p^2+(d-q)^2} = b.\]すなわち,\[p^2 + (d-q)^2 = b^2. \tag{2}\]
(C)$\angle ABC = \pi/6$ である.
頂点 $B$ において,
\[\small \overrightarrow{BA} = A-B = \bigl((p-L),\; d-(d-q)\bigr) = (p-L,\,q),\]\[\small \overrightarrow{BC} = C-B = \bigl((L-p)-L,\; 0-(d-q)\bigr) = (-p,\; q-d).\]よって内積は\[\small \overrightarrow{BA}\cdot\overrightarrow{BC} = (p-L)(-p)+q\,(q-d)= -p(p-L) + q(q-d).\]また $q-d = -(d-q)$ と書けるので,
\[\overrightarrow{BA}\cdot\overrightarrow{BC} = -p(p-L)-q(d-q).\]両ベクトルの大きさは $|\overrightarrow{BA}|=a,\; |\overrightarrow{BC}|=b$ であるから,
\[\frac{-p\bigl[(p-L)+q\tan\theta\bigr]}{ab} = \cos\frac{\pi}{6} = \frac{\sqrt{3}}{2},\]ただし,以下の(D)において示すように $d-q$ と $\tan\theta$ の関係を用いる.故に
\[(p-L) + q\tan\theta = -\frac{\sqrt{3}}{2}\frac{ab}{p}. \tag{3}\](後述の手順で符号の整合性が確認できる.)
(D)点 $C$ における角 $\theta=\angle BCG$ である.
点 $C=(L-p,0)$,$B=(L,d-q)$,$G=(L,0)$ より,
\[\small \overrightarrow{CB} = B-C = (L-(L-p),\, (d-q)-0) = (p,\, d-q),\]\[\small \overrightarrow{CG} = G-C = (L-(L-p),\, 0-0) = (p,\,0).\]よって,
\[\tan\theta = \frac{d-q}{p} \quad\Longrightarrow\quad d-q = p\tan\theta. \tag{4}\]すなわち,
\[d = q + p\tan\theta.\]を得る。
$(2)$式に$(4)$式 $d-q=p\tan\theta$ を代入すると,
\[p^2 + (p\tan\theta)^2 = b^2 \quad\Longrightarrow\quad p^2(1+\tan^2\theta)=b^2.\]すなわち,
\[p^2\sec^2\theta = b^2 \quad\Longrightarrow\quad p = b\cos\theta. \tag{5}\]
$(1)$式 より
\[(L-p)^2 = a^2-q^2\]\[\Longrightarrow\quad L-p = \sqrt{a^2-q^2}. \tag{1’}\]また,$(3)$式に$(4)$式および$(5)$式を代入すると,
\[(p-L) + q\tan\theta = -\frac{\sqrt{3}}{2}\frac{ab}{p}\]\[\therefore L-p = q\tan\theta + \frac{\sqrt{3}}{2}\frac{ab}{p}.\]さらに$(5)$式 $p=b\cos\theta$ が成り立つから,
\[L-p = q\tan\theta + \frac{\sqrt{3}\,a}{2\cos\theta}. \tag{6}\]
よって、\[\begin{aligned}L-p &= \frac{a}{2}\Bigl(\sin\theta+\sqrt{3}\cos\theta\Bigr), \\ q &= \frac{a}{2}\Bigl(\cos\theta-\sqrt{3}\sin\theta\Bigr)\end{aligned}\]と定めてもよいことが確認できる.
(実際,$$\begin{aligned}& \quad \left(\frac{a}{2}(\sin\theta+\sqrt{3}\cos\theta)\right)^2+\left(\frac{a}{2}(\cos\theta-\sqrt{3}\sin\theta)\right)^2 \\ &=\frac{a^2}{4}[\,(\sin\theta+\sqrt{3}\cos\theta)^2+(\cos\theta-\sqrt{3}\sin\theta)^2] \\ &=a^2\end{aligned}$$となる.)
(5) より $p = b\cos\theta$ であるから,
\[L = p + (L-p) = b\cos\theta + \frac{a}{2}\Bigl(\sin\theta+\sqrt{3}\cos\theta\Bigr).\]また,(4) と $q$ の値から,
\[\begin{aligned} d &= q + p\tan\theta \\ &= \frac{a}{2}\Bigl(\cos\theta-\sqrt{3}\sin\theta\Bigr) + b\cos\theta\tan\theta \\ &= \frac{a}{2}\Bigl(\cos\theta-\sqrt{3}\sin\theta\Bigr) + b\sin\theta.\end{aligned}\]よって長方形の面積は
\[\small \begin{aligned} S &= L\cdot d \\ &=\left[b\cos\theta+\frac{a}{2}\Bigl(\sin\theta+\sqrt{3}\cos\theta\Bigr)\right] \left[\frac{a}{2}\Bigl(\cos\theta-\sqrt{3}\sin\theta\Bigr)+b\sin\theta\right].\end{aligned}\]この積を展開し,三角恒等式 $\cos^2\theta = \dfrac{1+\cos2\theta}{2}$、$\sin^2\theta = \dfrac{1-\cos2\theta}{2}$、$\sin\theta\cos\theta = \dfrac{\sin2\theta}{2}$
を用いて整理すると,最終的に
\[S = \frac{ab}{2}+\left(\frac{b^2}{2}-\frac{a^2}{4}\right)\sin2\theta+\frac{a^2\sqrt{3}}{4}\cos2\theta.\]すなわち,
\[\boxed{S=\frac{b^2}{2}\sin2\theta+\frac{ab}{2}+\frac{a^2}{4}\Bigl(\sqrt{3}\cos2\theta-\sin2\theta\Bigr).}\]を得る。
(2)
(1) の式を
\[S(\theta)=\frac{ab}{2}+A\sin2\theta+B\cos2\theta\]ただし $A=\dfrac{b^2}{2}-\dfrac{a^2}{4}$、$B=\dfrac{a^2\sqrt{3}}{4}$
と見る.合成角の公式を用いると,
\[A\sin2\theta+B\cos2\theta = R\sin(2\theta+\phi),\]と表せる.ここで,
\[R=\sqrt{A^2+B^2}=\frac{1}{2}\sqrt{b^4-a^2b^2+a^4}\]とし、$\phi$ を $\tan \phi=\dfrac{B}{A}$、つまり $\tan \phi=\dfrac{a^2\sqrt{3}}{2b^2-a^2}$ となるような角とすると、\[S(\theta)=\frac{ab}{2}+R\sin(2\theta+\phi).\]となるが、平行四辺形が内接する条件から $\theta$ の取りうる範囲は
\[0<\theta<\frac{\pi}{6},\]すなわち $2\theta$ は
\[0<2\theta<\frac{\pi}{3}\]の範囲に制限される.よって $2\theta+\phi$ は $\phi<2\theta+\phi<\frac{\pi}{3}+\phi$ の区間をとる.この区間における $\sin(2\theta+\phi)$ の最大値の値は,$\phi$ の値により以下の2つの場合に分かれる.
(i) $\phi \ge \pi/6$ の場合
この条件は
\[\phi\ge\frac{\pi}{6} \quad\Longrightarrow\quad \frac{a^2\sqrt{3}}{2b^2-a^2}\ge\frac{1}{\sqrt{3}},\]すなわち
\[3a^2\ge 2b^2-a^2 \quad\Longrightarrow\quad b^2\le 2a^2.\]このとき,区間 $(\phi,\,\frac{\pi}{3}+\phi)$ 内に $\frac{\pi}{2}$ が含まれるため,$\sin(2\theta+\phi)$ の最大値は $1$ となる.
したがって,このときの最大値は
\[\begin{aligned}S_{\max}&=\frac{ab}{2}+R \\ &=\frac{ab}{2}+\frac{1}{2}\sqrt{b^4-a^2b^2+a^4}.\end{aligned}\]となる。
(ii) $\phi < \pi/6$ の場合
この場合は $b^2>2a^2$ となる.$2\theta$ の上限が $\pi/3$ であるため,$2\theta+\phi$ の最大値は $\dfrac{\pi}{3}+\phi$ となる.すなわち,
\[\sin(2\theta+\phi) \le \sin\Bigl(\frac{\pi}{3}+\phi\Bigr).\]直接計算すると,
\[\sin\Bigl(\frac{\pi}{3}+\phi\Bigr)=\frac{b^2\sqrt{3}}{2\sqrt{b^4-a^2b^2+a^4}},\]よって,このときの最大値は
\[\begin{aligned}S_{\max}&=\frac{ab}{2}+R\sin\Bigl(\frac{\pi}{3}+\phi\Bigr) \\ &=\frac{ab}{2}+\frac{1}{2}\sqrt{b^4-a^2b^2+a^4}\cdot\frac{b^2\sqrt{3}}{2\sqrt{b^4-a^2b^2+a^4}} \\ &=\frac{ab}{2}+\frac{\sqrt{3}\,b^2}{4}.\end{aligned}\]となる。
以上より,長方形の面積 $S$ のとりうる最大値は
\[\boxed{S_{\max}=\begin{cases}\displaystyle \frac{ab+\sqrt{b^4-a^2b^2+a^4}}{2} \quad &\text{if } b^2\le 2a^2,\\[2mm] \displaystyle \frac{ab}{2}+\frac{\sqrt{3}\,b^2}{4} \quad &\text{if } b^2>2a^2.\end{cases}}\]と求められる。
面積$S$の式を得るところまではミスなく行けるかと思います。(2)では場合分けが頭からすっぽ抜けてしまった人は多かったかもしれません。$\angle ABC = \dfrac{\pi}{6}$ という制約が効いてくるため、$S$の取りうる範囲には制限が生じます。図形的なイメージができていると面積$S$の定義域の変化に気が付けたかもしれません。
因みに、本問はOpenAI o1 proでもDeepSeekのDeepThinkでも正答は得られていませんでした。o3-mini-highでは最後の場合分けが上手くいっていないこと以外は正答を得られていました。o3本体はさらに数理的推論能力がアップしていると言われていますので、リリースが待ち遠しいですね。
» 【参考:図形の描画スクリプト】
[asy]
import graph;
import geometry;
import math;
size(200);
// パラメータ
real a = 2, b = 6, t = 4;
// 長方形の頂点
pair E = (0,0);
pair H = (a,0);
pair G = (a,b);
pair F = (0,b);
// 平行四辺形ABCDの頂点(長方形の辺上に配置)
pair A = F + (0,-t * sqrt(3)/3);
pair B = F + (t * 1/8, 0);
pair C = H + (0, t * sqrt(3)/3);
pair D = H + (- t * 1/8, 0);
// 辺の描画
draw(E--H--G--F--cycle, linewidth(0.8) + dashed); // 長方形
draw(A--B, linewidth(0.8));
draw(B--C, linewidth(0.8));
draw(C--D, linewidth(0.8));
draw(D--A, linewidth(0.8));
// 各点の描画
dot(A);
dot(B);
dot(C);
dot(D);
dot(E);
dot(F);
dot(G);
dot(H);
// ラベル
label("$E$", E, SW);
label("$H$", H, SE);
label("$G$", G, NE);
label("$F$", F, NW);
label("$A$", A, W);
label("$B$", B, N);
label("$C$", C, NE);
label("$D$", D, S);
label("$\theta$", A + (0.2,-0.8), S);
label("$\theta$", C + (-0.2,0.8), N);
label("$\frac{5}{6}\pi$", A + (0.4,-0.0), E);
label("$\frac{\pi}{6}$", B + (0.07,-0.35), S);
label("$\frac{\pi}{2}-\theta$", B + (0.15,-0.05), SE);
[/asy]
» 閉じる
(2025/02/28追記)記事のタイトルに誤りがあったため修正。これに伴いパーマリンクも修正しました。
(2026/01/04追記)数式のスタイルを一部変更。
