方程式と関数の違いを理解しよう！

「方程式」と「関数」は中学数学で登場する概念ですが、これらの違いを正確に把握できている学生は高校生であっても多くない気がします。今回の記事は、方程式と関数の違いを理解を目指す中学生や高校生の方のための記事です。

 

 関数とは何だったか

中学数学で学ぶ関数と言えば、

1次関数、2次関数、反比例の関数（双曲線）、ガウス関数

などです。教科書には関数の定義がちゃんと書いてあります。

文章にすると小難しく感じられますが、図にすると次のようなイメージです。

「$x$の値を定めるとそれに対応した$y$がただ一つに定まる」というのは図にすると次のようなイメージです。

このように、$x$の値に応じて$y$の値をただ一つ定めるものを「関数」（function）もしくは「写像」（mapping）と言います。ある関数 $y=f(x)$ に$x$を代入すると$y$という値が返ってきます。「関数とは値を代入したら何らかの値が返ってくるもの」というイメージを持ってください。（この場合はもっと言うと「1価関数」という名前が付いていますが、難しいので覚えなくて良いです）

※「写像」というのは中学生や高校生の方にとっては聞き慣れない単語だと思いますが、「関数」をより広い枠組みで捉えたときに、ある集合のある要素に対して「像を写す」という意味合いでそのように呼ぶことがあります･･･が、知らなくても問題ありません。

 

 関数の周りにある「方程式」

例えば、$x=2$ のとき、関数$f(x)$が $y=4$ という値を取る場合は$$f(2)=4$$と書きます。これはただ単に、ある値を関数に代入したときの式であり、「$x=2$ という値を代入したときに $4$ という値が返される」という事実を説明しているだけの式です。因みに、関数の文字として $f$ がよく使われますが、これは “function” の頭文字から採られているものです。

一方で、ある未知数$x$があって、そのとき関数$f(x)$が $y=4$ という値を取る場合は$$f(x)=4$$と書きます。このような未知数を求めるための等式を「方程式」（equation）と呼びます。（「関数」の主役が$y$だとしたら、「方程式」の主役は$x$、といったようなイメージでしょうか）

例えば、一次関数 $y=2x+1$ があり、$y=4$ となるような$x$を求めたいときは$$2x+1=4$$という方程式を解くことになります。これは「関数」ではなく「方程式」であることに注意しましょう。

※細かいことですが、この方程式は $4=2x+1$ と書いても全く同じ意味になります。式を描く順番には特に意味はありません。

---

さて、この $2x+1=4$ という方程式はどこから出てきたのでしょうか？ 皆さんは無意識のうちに $2x+1=4$ という方程式を立ててしまうかもしれませんが、この方程式の意味を改めてよく考えることは大切です。

$f(x)=2x+1$ のとき、一次関数 $y=f(x)$ のグラフは次のようになります。

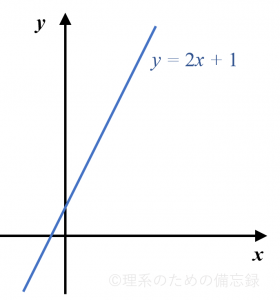
これは関数です。方程式ではありません。

いま、$y=4$ となるような$x$を求めたいのですが、この $y=4$ というのは$x$軸に平行な直線です。これを書き加えると次のようになります。

この２直線（２つの関数）の交点に注目すると、$x$座標が $x=\dfrac{3}{2}$ となっています。このことは「連立方程式$$\left\{\begin{array}{l}
y=2 x+1 \\
y=4
\end{array}\right.$$を解く」という操作が「２直線の交点を求める」という操作に対応していることを意味します。

つまり、方程式 $2x+1=4$ は２つの「関数」の式を連立することで得られていたのです。このように考えると、「方程式」は幾つかの関数の式を組み合わせて得られるもので、「方程式」と「関数」は別物であることが理解できると思います。

ただし両者の間に全く関係が無い訳ではなく、上記で見たように関数に関する情報を得るために方程式が作られます。これは一次関数に限った話ではなく、二次関数や三次関数など、他の関数でも同じです。

 

 まとめ

以上のことを踏まえると、関数（$y=2x+1$ など）は

「値を代入したら何らかの値が返ってくるもの」

であり、方程式（$2x+1=4$ など）は

「未知数を決定するために（関数の式から）作った等式」

と説明できます。両者は式の見た目がよく似ていますが、使い方や成り立ちが異なります。以上のことを正しく理解しておきましょう！

 

---

（2021/09/30追記：本文の表現･スタイルを一部変更）