座標平面上で面積を求める積分をする際、大抵の場合は変数をxとして計算することが多いですが、世の中の入試問題にはyで積分計算が可能な問題もあります。
《問題》
2つの曲線 $C_{1}: y=x^{2}-\dfrac{3}{2}$ と $C_{2}: y^{2}=-2 x+\dfrac{9}{4}$ を考える。
(1)$C_1$、$C_2$ の共有点をすべて求めよ。
(2)2つの領域 $y \geqq x^2-\dfrac{3}{2}$ と $y^2 \leqq -2x+\dfrac{9}{4}$ の共通部分 $W$ の面積 $S$ を求めよ。
(大阪医科大学2020年 後期第2問)
《考え方》
(1)は簡単ですね。問題は(2)です。理系しか受けない試験なので$x$で積分しても良いのですが、$y$で積分しても良いのです・・・。
● ● ●
解答例
(1)
$C_2$ の式に $C_1$ の式を代入して$$\left(x^{2}-\dfrac{3}{2}\right)^{2}=-2 x+\dfrac{9}{4}$$ $$\therefore x^{4}-3 x^{2}+\frac{9}{4}=2 x+\dfrac{9}{4}$$ $$\therefore x^{4}-3 x^{2}-2 x=0$$ $$\therefore x(x-1)^{2}(x+2)=0$$ $$\therefore x=-2,\,0,\,1$$を得る。よって共有点は $\color{red}{\left(-2, \dfrac{5}{2}\right)}$、$\color{red}{\left(0,-\dfrac{3}{2}\right)}$、$\color{red}{\left(1,-\dfrac{1}{2}\right)}$(接点)となる。
(2)~ $x$で積分
$C_1$、$C_2$ の位置関係は以下のようになる。
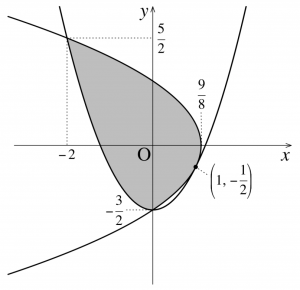
$C_1$、$C_2$ の頂点はそれぞれ$$\left(0,-\dfrac{3}{2}\right),\left(\dfrac{9}{8}, 0\right)$$である。共通部分 $W$ は図の網掛け部分であり、その面積 $S$ は$$\small \begin{align}
S &=\int_{0}^{\frac{9}{8}} 2 \sqrt{-2 x+\frac{9}{4}} d x+\int_{-2}^{0}\left(\sqrt{-2 x+\frac{9}{4}}+\frac{3}{2}-x^{2}\right) d x \\
&=\left[-\frac{2}{3}\left(-2 x+\frac{9}{4}\right)^{\frac{3}{2}}\right]_{0}^{\frac{9}{8}} \\ & \quad \quad +\left[-\frac{1}{3}\left(-2 x+\frac{9}{4}\right)^{\frac{3}{2}}\right]_{-2}^{0}+\left[\frac{3}{2} x-\frac{x^{3}}{3}\right]_{-2}^{0} \\
&=\frac{2}{3}\left(\frac{9}{4}\right)^{\frac{3}{2}}-\frac{1}{3}\left(\frac{9}{4}\right)^{\frac{3}{2}}+\frac{1}{3}\left(\frac{25}{4}\right)^{\frac{3}{2}}-\frac{8}{3}+3 \\
&=\color{red}{\frac{20}{3}}
\end{align}$$と求められる。
(2)別解 ~ $x$と$y$で積分
以下のように、直線 $l:y=-2x-\dfrac{3}{2}$ で$W$を分割する。
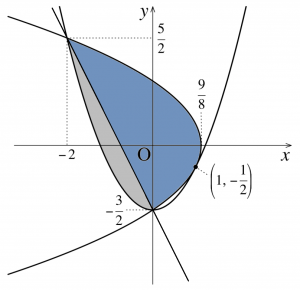
このとき、$W$の部分のうち $l$ の上側の面積を$S_1$、下側の面積を$S_2$とすると、$l:x=-\dfrac{1}{2}y-\dfrac{3}{4}$ および $C_{2}: x=-\dfrac{1}{2}y^{2}+\dfrac{9}{8}$ より、$$\small \begin{align}
S_1 &=\int_{-\frac{3}{2}}^{\frac{5}{2}} \left\{\left(-\dfrac{1}{2}y^{2}+\dfrac{9}{8}\right)-\left(-\dfrac{1}{2}y-\dfrac{3}{4}\right)\right\} d y \\
&=\int_{-\frac{3}{2}}^{\frac{5}{2}} \left(-\dfrac{1}{2}y^{2}+\dfrac{1}{2}y+\dfrac{15}{8}\right) d y \\
&=-\dfrac{1}{2}\left[\dfrac{1}{3}y^{3}-\dfrac{1}{2}y^{2}-\dfrac{15}{4}y\right]_{-\frac{3}{2}}^{\frac{5}{2}} \\
&=\dfrac{16}{3}
\end{align}$$また、$$\small \begin{align}
S_2 &=\int_{-2}^{0} \left\{\left(-2x-\dfrac{3}{2}\right)-\left(x^{2}-\dfrac{3}{2}\right)\right\} d x \\
&=\int_{-2}^{0} \left(-x^{2}-2x\right) d x \\
&=-\left[\dfrac{1}{3}x^{3}+x^{2}\right]_{-2}^{0} \\
&=\dfrac{4}{3}
\end{align}$$となるから、$$S=S_1+S_2=\color{red}{\frac{20}{3}}$$と求められる。
(コメント)
計算は面倒になりますが、数Ⅲの知識が無くても解答可能です。ルートの積分ができなければ別解のように解くことになります。
