プログラミング言語Pythonを利用して3D曲線を描画する方法を紹介します。ここでは例として「ローレンツアトラクタ」を描画してみます。
ローレンツ方程式とは
以下の非線型常微分方程式を「ローレンツ方程式」と言います。$$\left\{\begin{array}{l}\dfrac{d x}{d t}=-p x+p y \\ \dfrac{d y}{d t}=-x z+r x-y \\ \dfrac{d z}{d t}=x y-b z\end{array}\right.$$これはマサチューセッツ工科大学の気象学者、エドワード・N・ローレンツ (Edward N. Lorenz) によって1963年の論文中で言及されたのが初出で、解が初期値鋭敏性を持ち、カオス的な挙動を示すことで知られています。
解の挙動は3つの定数 $p,\, r,\, b$ によって定まり、ローレンツの論文中で用いられた $p = 10$、$r = 28$、$b = 8/3$ という組が有名です。このとき初期値を$(1.0, 1.0, 1.0)$として軌跡を描画すると次のようになります。
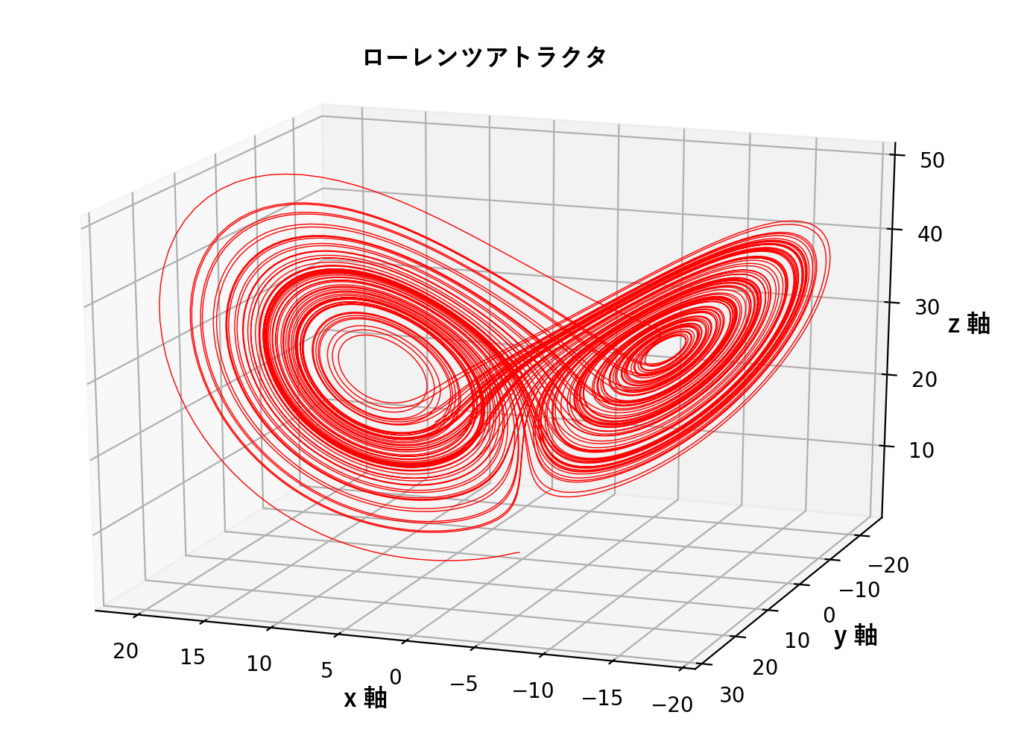
これを「ローレンツ・アトラクタ」と言います。
※方程式を満たすように時間発展する空間上の点は、空間内の一定の領域に引き付けられるように軌跡を描くことがあり、これを「アトラクタ」(attractor)と呼びます。
ローレンツアトラクタの3D描画
ローレンツアトラクタを立体的な曲線として描画するPythonのコード例を示します。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d, Axes3D
def lorenz(x, y, z, s=10, r=28, b=8/3):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
# 時間の設定
dt = 0.005
num_steps = 20000
# 空の配列を生成
xs = np.empty(num_steps + 1)
ys = np.empty(num_steps + 1)
zs = np.empty(num_steps + 1)
# 初期条件
xs[0], ys[0], zs[0] = (1., 1., 1)
# 点列の座標生成
for i in range(num_steps):
x_dot, y_dot, z_dot = lorenz(xs[i], ys[i], zs[i])
xs[i + 1] = xs[i] + (x_dot * dt)
ys[i + 1] = ys[i] + (y_dot * dt)
zs[i + 1] = zs[i] + (z_dot * dt)
# 曲線の3Dプロット
ax = plt.figure(figsize=(6,4), dpi=200).add_subplot(projection='3d')
ax.view_init(elev=20, azim=110)
ax.plot(xs, ys, zs, lw=0.5)#, c="r")
ax.set_xlabel("x axis", size=12)
ax.set_ylabel("y axis", size=12)
ax.set_zlabel("z axis", size=12)
ax.set_title("Lorenz Attractor", size=12)
plt.show()
これを実行すると以下のような図が得られます。描画に時間が掛かる場合は図のサイズや解像度(”dpi”の値)を小さくして下さい。
ラベルに日本語を使う
ラベルに日本語を使う場合は、ttfファイルのパスを指定する必要があります。以下の例では游ゴシック(yugothib.ttf)を使っています。ttfファイルはフリーのものを適当にダウンロードして使って下さい(例えばこのサイトからダウンロードすることができます)。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d, Axes3D
from matplotlib.font_manager import FontProperties # フォントに関するモジュール
from matplotlib.ticker import ScalarFormatter # 軸フォーマットに関するモジュール
fp = FontProperties(fname='C:/Users/[user]/AppData/Local/Microsoft/Windows/Fonts/yugothib.ttf') # パスはご自分で指定して下さい
def lorenz(x, y, z, s=10, r=28, b=8/3):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
# 時間の設定
dt = 0.005
num_steps = 20000
# 空の配列を生成
xs = np.empty(num_steps + 1)
ys = np.empty(num_steps + 1)
zs = np.empty(num_steps + 1)
# 初期条件
xs[0], ys[0], zs[0] = (1., 1., 1)
# 点列の座標生成
for i in range(num_steps):
x_dot, y_dot, z_dot = lorenz(xs[i], ys[i], zs[i])
xs[i + 1] = xs[i] + (x_dot * dt)
ys[i + 1] = ys[i] + (y_dot * dt)
zs[i + 1] = zs[i] + (z_dot * dt)
# 曲線の3Dプロット
ax = plt.figure(figsize=(6,4), dpi=200).add_subplot(projection='3d')
ax.view_init(elev=20, azim=110)
ax.plot(xs, ys, zs, lw=0.5)#, c="r")
ax.set_xlabel("x 軸",fontproperties=fp, size=12)
ax.set_ylabel("y 軸",fontproperties=fp, size=12)
ax.set_zlabel("z 軸",fontproperties=fp, size=12)
ax.set_title("ローレンツアトラクタ",fontproperties=fp, size=12)
plt.show()
連続的にカラーリングする
少し複雑ですが曲線を連続的にカラーリングすることも可能です。
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import colors
def lorenz(x, y, z, s=10, r=28, b=8/3):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
# 時間の設定
dt = 0.005
num_steps = 20000
# 空の配列を生成
xs = np.empty(num_steps + 1)
ys = np.empty(num_steps + 1)
zs = np.empty(num_steps + 1)
# 初期条件
xs[0], ys[0], zs[0] = (1., 1., 1)
# 曲線の3Dプロット
ax = plt.figure(figsize=(12,8), dpi=200).add_subplot(projection='3d')
ax.view_init(elev=20, azim=110)
# 点列の座標生成
for i in range(num_steps):
x_dot, y_dot, z_dot = lorenz(xs[i], ys[i], zs[i])
xs[i + 1] = xs[i] + (x_dot * dt)
ys[i + 1] = ys[i] + (y_dot * dt)
zs[i + 1] = zs[i] + (z_dot * dt)
# 線分の描画(描画範囲のx座標で正規化)
cn = colors.Normalize(xs.min(), xs.max())
# cn = colors.Normalize(0.0, num_steps)
for i in range(num_steps):
ax.plot(xs[i:i+2], ys[i:i+2], zs[i:i+2], color=plt.cm.viridis(cn(xs[i])), lw=0.5)
# ax.plot(xs[i:i+2], ys[i:i+2], zs[i:i+2], color=plt.cm.viridis(cn(i)), lw=0.5)
ax.set_xlabel("x axis", size=12)
ax.set_ylabel("y axis", size=12)
ax.set_zlabel("z axis", size=12)
ax.set_title("Lorenz Attractor", size=12)
plt.show()
これを実行すると以下のような図が得られます。
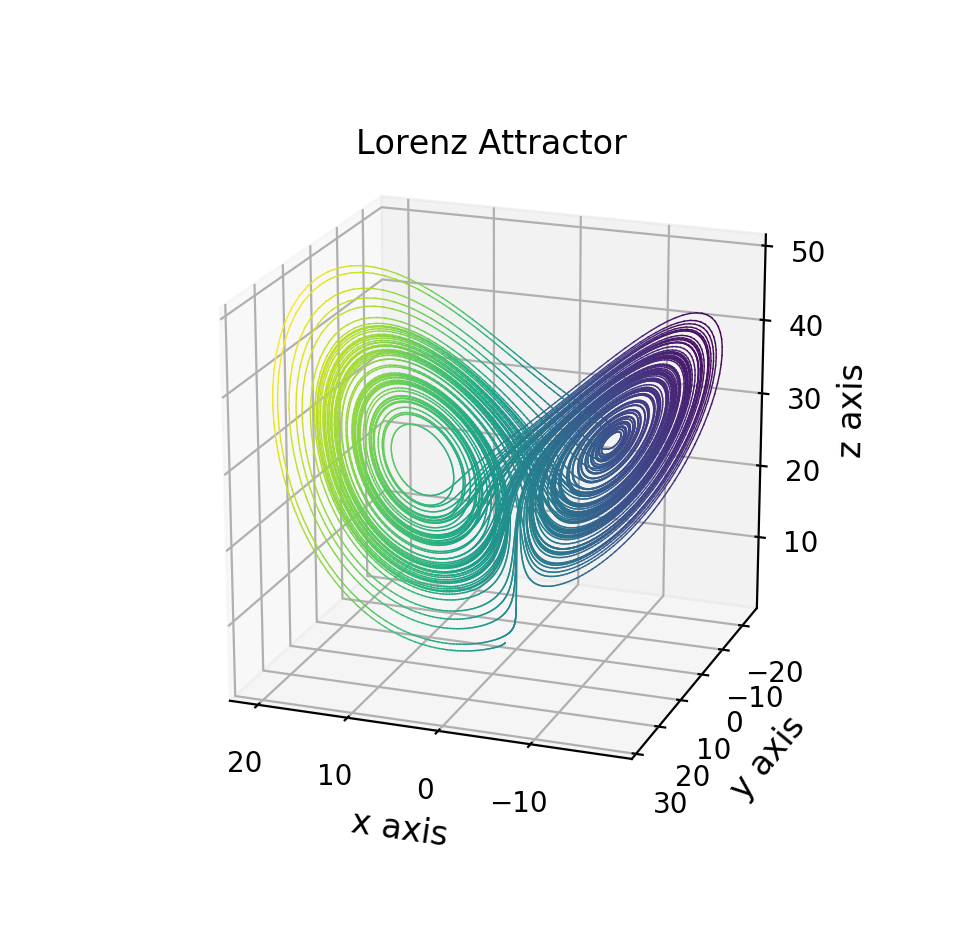 図.連続的なカラーリング($x$方向)
図.連続的なカラーリング($x$方向)
ステップ数に比例するように色相を変化させることもできます。上の例では$x$座標の最小~最大の範囲を $[0,\,1]$ に規格化して描画していますが、ステップ数を規格化して表示した場合は以下のようになります。
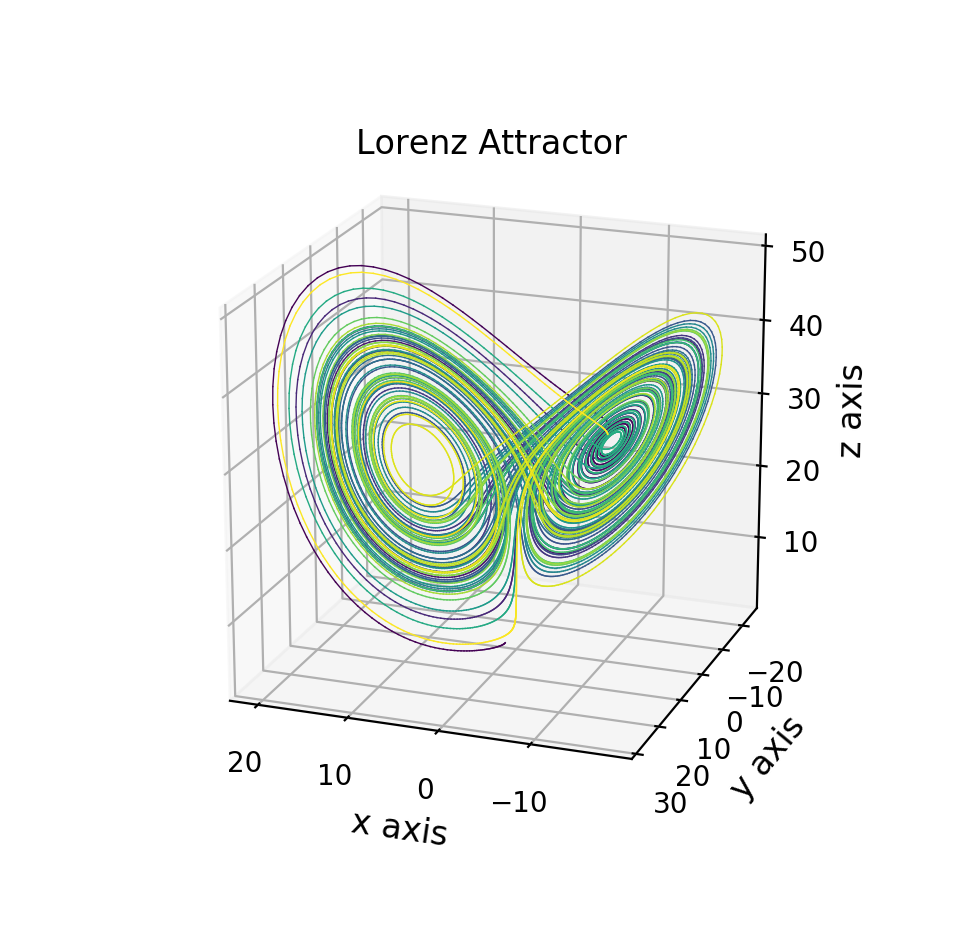 図.連続的なカラーリング(ステップ数)
図.連続的なカラーリング(ステップ数)
» コード例
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import colors
def lorenz(x, y, z, s=10, r=28, b=8/3):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
# 時間の設定
dt = 0.005
num_steps = 20000
# 空の配列を生成
xs = np.empty(num_steps + 1)
ys = np.empty(num_steps + 1)
zs = np.empty(num_steps + 1)
# 初期条件
xs[0], ys[0], zs[0] = (1., 1., 1)
# 曲線の3Dプロット
ax = plt.figure(figsize=(12,8), dpi=200).add_subplot(projection='3d')
ax.view_init(elev=20, azim=110)
# 点列の座標生成
for i in range(num_steps):
x_dot, y_dot, z_dot = lorenz(xs[i], ys[i], zs[i])
xs[i + 1] = xs[i] + (x_dot * dt)
ys[i + 1] = ys[i] + (y_dot * dt)
zs[i + 1] = zs[i] + (z_dot * dt)
# 線分の描画(ステップ数で正規化)
# cn = colors.Normalize(xs.min(), xs.max())
cn = colors.Normalize(0.0, num_steps)
for i in range(num_steps):
# ax.plot(xs[i:i+2], ys[i:i+2], zs[i:i+2], color=plt.cm.viridis(cn(xs[i])), lw=0.5)
ax.plot(xs[i:i+2], ys[i:i+2], zs[i:i+2], color=plt.cm.viridis(cn(i)), lw=0.5)
ax.set_xlabel("x axis", size=12)
ax.set_ylabel("y axis", size=12)
ax.set_zlabel("z axis", size=12)
ax.set_title("Lorenz Attractor", size=12)
plt.show()
» 閉じる
軌跡は一定の領域に収まっていますが、色が入り乱れていて予測不能な軌道を描くことが視覚的に理解できます。また、初期値鋭敏性もカラーリングすることで分かりやすくなります(ほんの僅かに初期値を変えただけで周回する領域が全く異なる結果になります)。
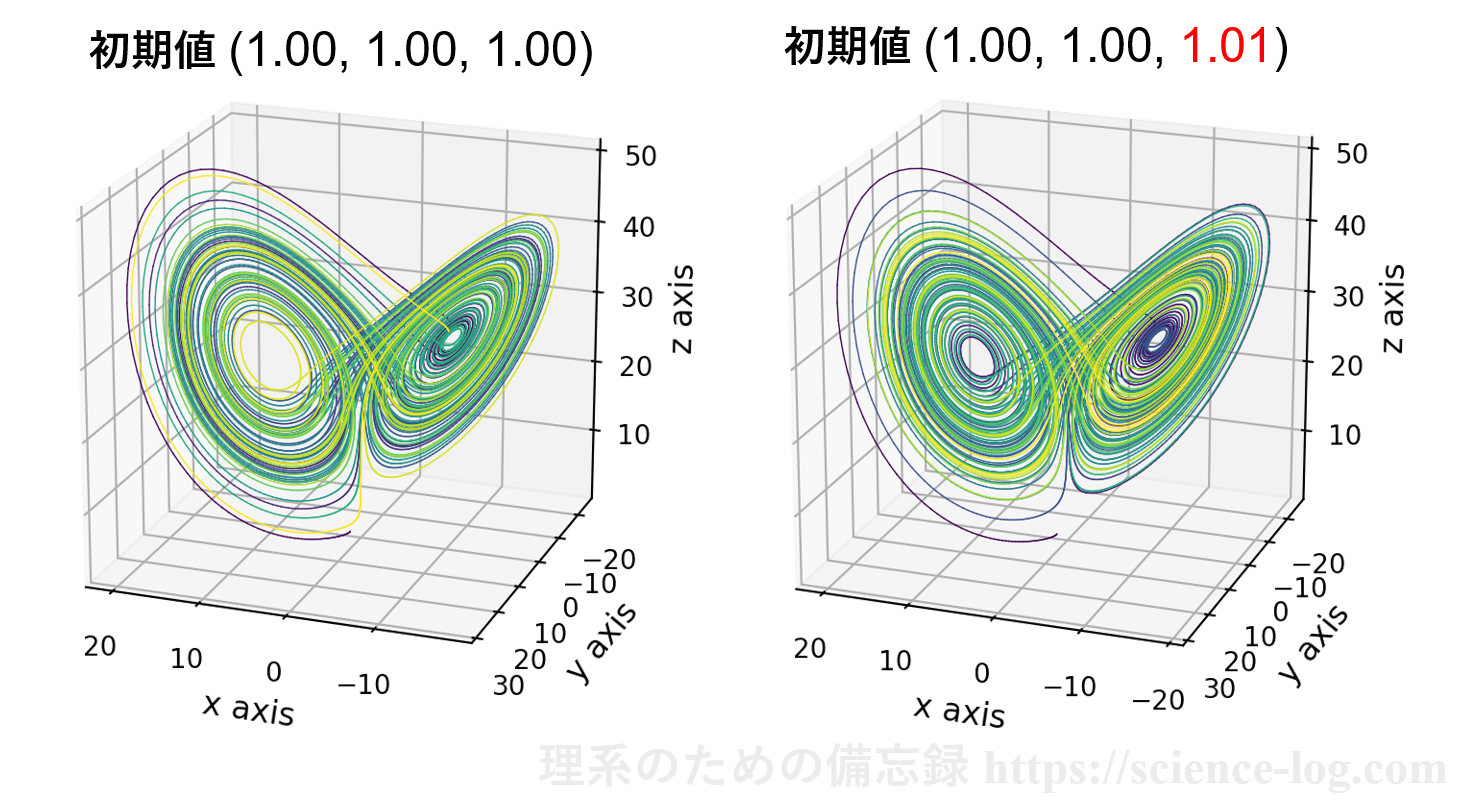 図.ローレンツアトラクタの初期値鋭敏性
図.ローレンツアトラクタの初期値鋭敏性
(刻み幅:0.005、ステップ数:20000)
平面を透明化&背景色を変える
「w_xaxis.set_pane_color((0., 0., 0., 0.))」と指定すると$x$軸に垂直な面の色が透明化できます(括弧内の数値はRGBAなのでAの値がゼロなら透明になる)。他の軸についても同じように指定すれば背景の面がすべて透明化されます。
ここでは図の背景色を黒色にしてみます。「plt.style.use(‘dark_background’)」を利用します。
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import colors
def lorenz(x, y, z, s=10, r=28, b=8/3):
x_dot = s*(y - x)
y_dot = r*x - y - x*z
z_dot = x*y - b*z
return x_dot, y_dot, z_dot
# 時間の設定
dt = 0.005
num_steps = 20000
# 空の配列を生成
xs = np.empty(num_steps + 1)
ys = np.empty(num_steps + 1)
zs = np.empty(num_steps + 1)
# 初期条件
xs[0], ys[0], zs[0] = (1., 1., 1.005)
# 曲線の3Dプロット
plt.style.use('dark_background')
ax = plt.figure(figsize=(12,6), dpi=200).add_subplot(projection='3d')
ax.view_init(elev=20, azim=110)
ax.w_xaxis.set_pane_color((0., 0., 0., 0.))
ax.w_yaxis.set_pane_color((0., 0., 0., 0.))
ax.w_zaxis.set_pane_color((0., 0., 0., 0.))
# 点列の座標生成
for i in range(num_steps):
x_dot, y_dot, z_dot = lorenz(xs[i], ys[i], zs[i])
xs[i + 1] = xs[i] + (x_dot * dt)
ys[i + 1] = ys[i] + (y_dot * dt)
zs[i + 1] = zs[i] + (z_dot * dt)
# 線分の描画
cn = colors.Normalize(xs.min(), xs.max())
# cn = colors.Normalize(0.0, num_steps)
for i in range(num_steps):
ax.plot(xs[i:i+2], ys[i:i+2], zs[i:i+2], color=plt.cm.viridis(cn(xs[i])), lw=0.5)
# ax.plot(xs[i:i+2], ys[i:i+2], zs[i:i+2], color=plt.cm.viridis(cn(i)), lw=0.5)
plt.show()
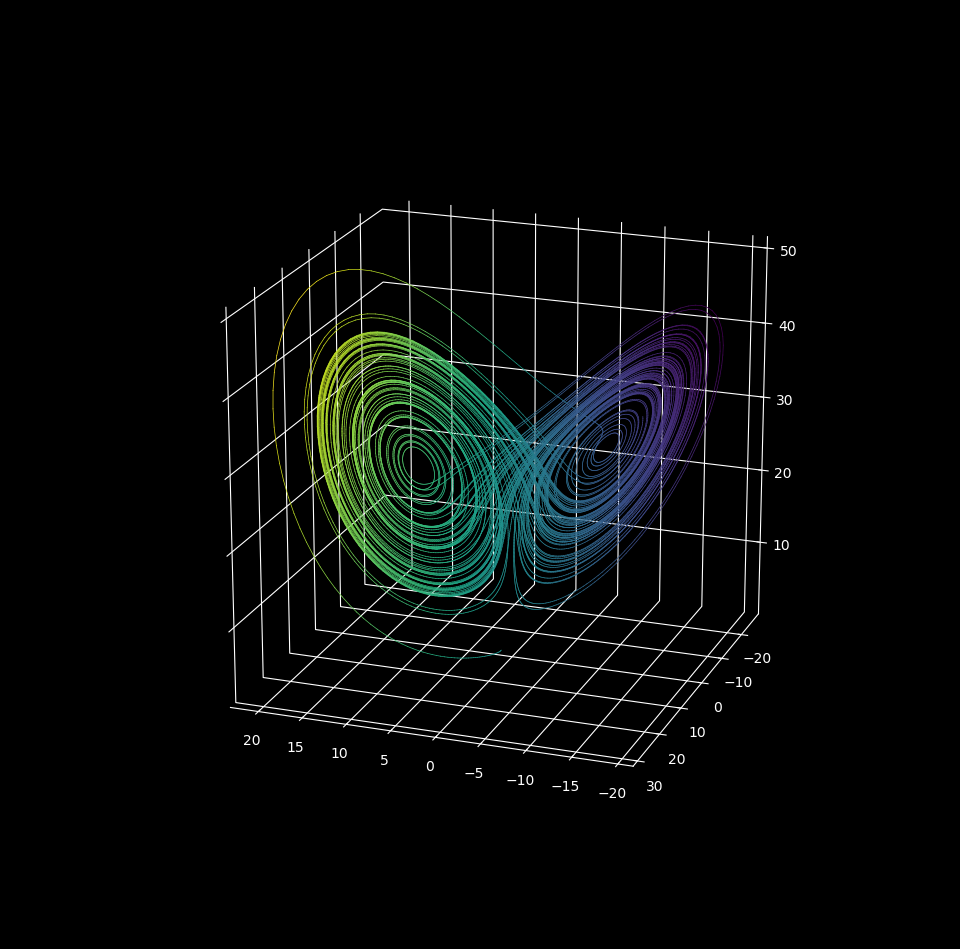 図.黒色背景の3Dプロット
図.黒色背景の3Dプロット
なお、「plt.rcParams[‘axes.facecolor’] = ‘k’」とするとグラフの背景色を黒色にできますが、画像全体で見ると余白に白色の部分が残ってしまいます。

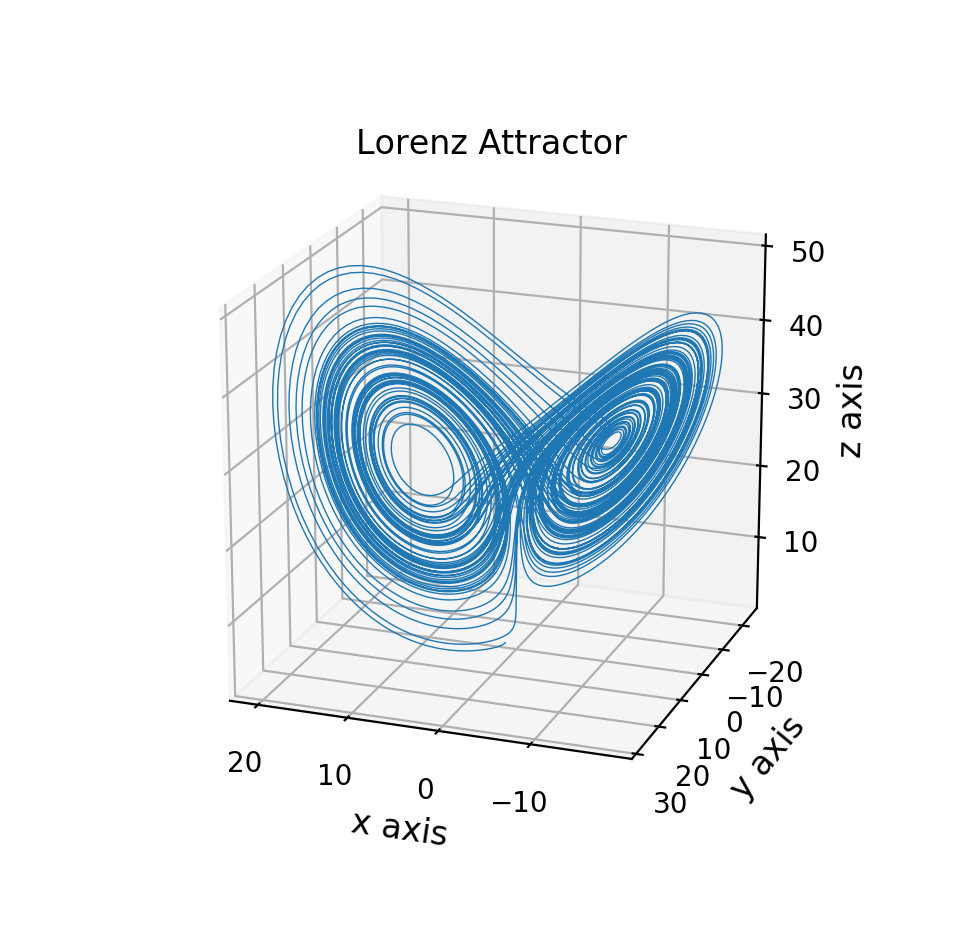 図.ローレンツアトラクタの3D描画
図.ローレンツアトラクタの3D描画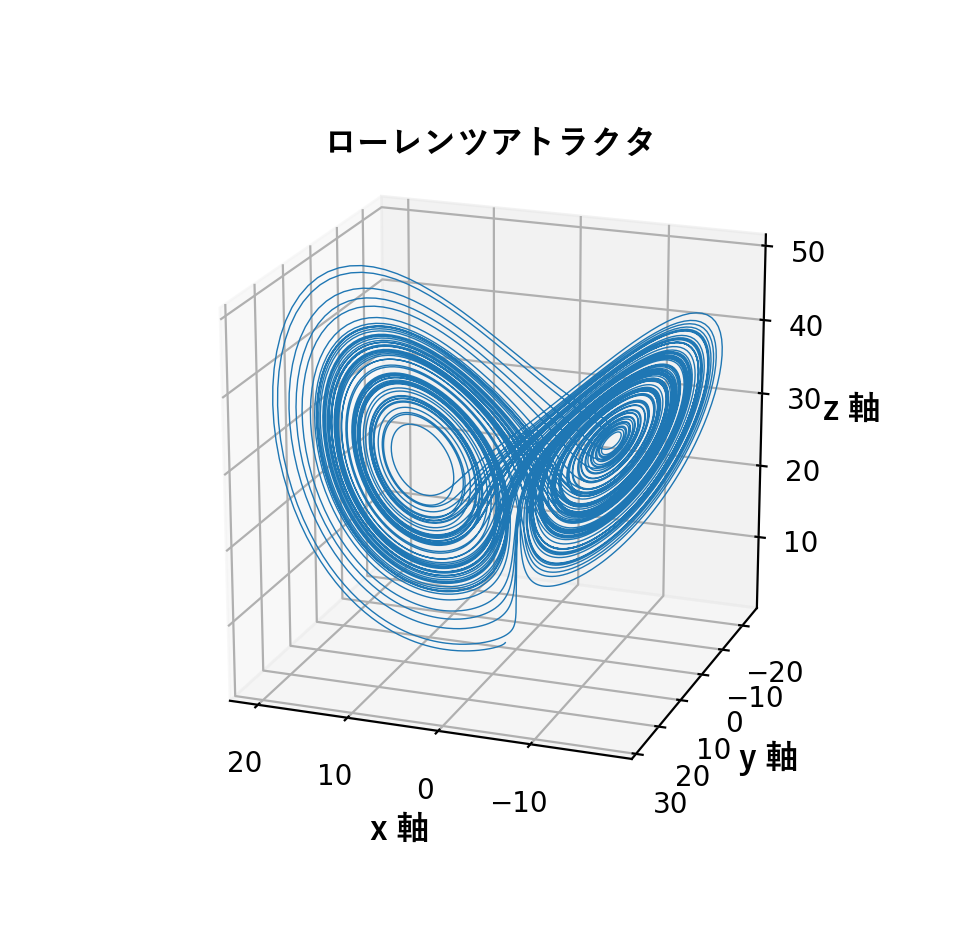 図.日本語ラベル
図.日本語ラベル