Python用のグラフ描画ライブラリ「matplotlib」を使ってグラフを描く方法の総まとめメモです。基本的なプロットを中心に、色々なグラフを描いてみましょう。
目次
・matplotlibの基本と2つの流儀
・色・線種・マーカーの指定
・折れ線&曲線のグラフ
・棒グラフ
・円グラフ
・ヒストグラム
・散布図とカラーバー
・ヒートマップ
・複数の線を表示する
・等高線&濃淡のある等高線
・3Dのグラフを表示する
・複数のグラフを並べる
・最後に
matplotlibの基本と2つの流儀
matplotlibはPythonで静的なプロットやアニメーション、インタラクティブな可視化を実現するための包括的なライブラリです。Pythonでグラフを描画するときは、取り敢えずmatplotlibを使っておけば間違いありません。
ここでは既にnumpyおよびmatplotlibライブラリが導入されているものとして使い方を解説していきます。導入自体はpipインストーラなどで可能ですし、Anacondaで環境構築している場合はcondaで導入可能です。
matplotlibライブラリは以下のようにインポートします。matplotlibに梱包されているpyplotモジュールはpltという名称で置換するのが慣例になっています。
import matplotlib as mpl import matplotlib.pyplot as plt
例えば折れ線グラフは次のようにすれば表示できます。$(x,y)$の点列を黒線で繋いだだけのプロットです。以下のコードでは座標の値をリストで渡していますが、numpyの配列としても渡すことができます。
import matplotlib.pyplot as plt # pyplotモジュールを"plt"という名前でインポートする x = [0, 1, 2, 3] # x座標 y = [1, 5, 2, 6] # y座標 plt.plot(x, y, color="k") # 点列(x,y)を黒線で繋いだプロット plt.show() # プロットを表示
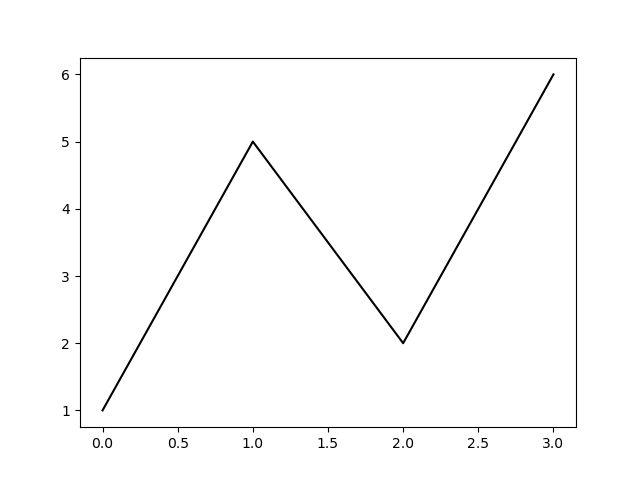
ところで、matplotlibにはグラフを作る上で2つの流儀が存在するということは知っておくべき事項です。
一つは「Pyplotインターフェース」と呼ばれるもので、MATLABに近い書き方ができます。元々matplotlibはMATLABに準ずる描画機能をPythonで実現するために開発されてきた経緯があり、pyplotモジュールから直接関数を呼び出す方式なので書き方はこちらの方がシンプルです。ただし簡単に描ける分、プロットの自由度は限定的です。
もう一つは「オブジェクト指向インターフェース」と呼ばれるものです。この記法は下図のように階層構造にしてグラフを描画するもので、こちらの方が図の細かい調整には向いています。イメージとしては、Figureオブジェクト(画板)の中にAxesオブジェクト(台紙)があり、その上にタイトルや凡例、軸ラベルなどのオブジェクトを出力するという形でプロットを表示します。
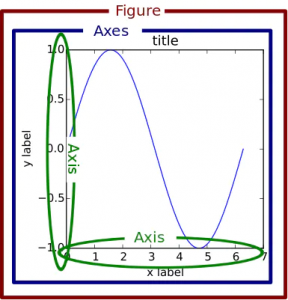
ネット上のコードはこれら2つの記法が綯い交ぜになっており、コピペしただけでは狙った挙動にならず変な所でハマってしまう危険性があります。こうしたことを避けるためにも、まずはmatplotlibの記法には2種類の流儀が存在することをよく覚えておきましょう。
ここでは簡便なPyplotインターフェースを主に採用してサンプルコードを掲載していますが、見栄えを重視するのであれば、普段からオブジェクト指向インターフェースを利用して慣れておくことを推奨します。特に理由が無ければオブジェクト指向インターフェースに統一すべきという意見もあります。
色・線種・マーカーの指定
色や線種、マーカーはplotメソッドの引数として指定します。例えば以下のようにとすると、青色の実線で関数 $y=x^2$ が描かれます。
import numpy as np import matplotlib.pyplot as plt x = np.arange(0.0, 5.0, 0.02) plt.plot(x, x**2, 'b-') plt.show()
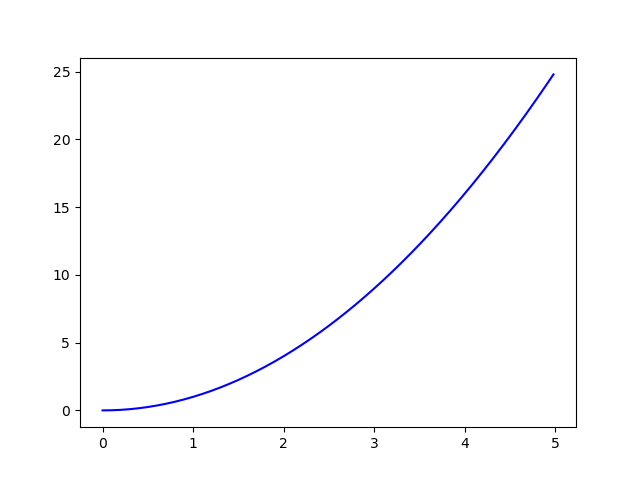
matplotlibではカラーコードを指定すればどんな色でも使えますが、よく使われる色には特別な名前が付けられています。使用できる色と名前は以下の通りです。



(公式ドキュメントはこちら)
また、線種の一覧は以下の通りです。
| 記法 | 線種 |
| ls=”:” | 点線 |
| ls=”-.” | 一点鎖線 |
| ls=”–“ | 破線 |
| ls=”-“ | 実線 |
(公式ドキュメントはこちら)
matplotlibには以下のように多数のマーカーが用意されています。
| 記法 | マーカー |
| marker=”.” | 点 |
| marker=”,” | ピクセル |
| marker=”o” | 丸 |
| marker=”v” | 下三角形 |
| marker=”^” | 三角形 |
| marker=”<“ | 左三角形 |
| marker=”>” | 右三角形 |
| marker=”s” | 四角形 |
| marker=”p” | 五角形 |
| marker=”h” | 六角形 |
| marker=”8″ | 八角形 |
(つづき)
| 記法 | マーカー |
| marker=”*” | 星 |
| marker=”1″ | Y |
| marker=”2″ | Y(上下反転) |
| marker=”3″ | Y(90度時計回り) |
| marker=”4″ | Y(90度反時計周り) |
| marker=”+” | + |
| marker=”x” | x |
| marker=”X” | x(filled) |
| marker=”D” | ひし形 |
| marker=”d” | 細いひし形 |
| marker=”” | マーカー無し |
(公式ドキュメントはこちら)
例えば以下のようなコードを走らせると下図のようなプロットが得られます。
import numpy as np import matplotlib.pyplot as plt def f(t): return np.exp(-t) * np.cos(2*np.pi*t) x1 = np.arange(0.0, 5.0, 0.02) x2 = np.arange(0.0, 5.0, 0.1) ax1 = plt.subplot(2,2,1) ax2 = plt.subplot(2,2,2) ax3 = plt.subplot(2,2,3) ax4 = plt.subplot(2,2,4) ax1.plot(x1, f(x1), 'k-', x2, f(x2), 'b.') ax2.plot(x1, f(x1), 'r--', x2, f(x2), 'rx') ax3.plot(x1, f(x1), 'k-.') ax4.plot(x1, f(x1), 'b:') plt.show()
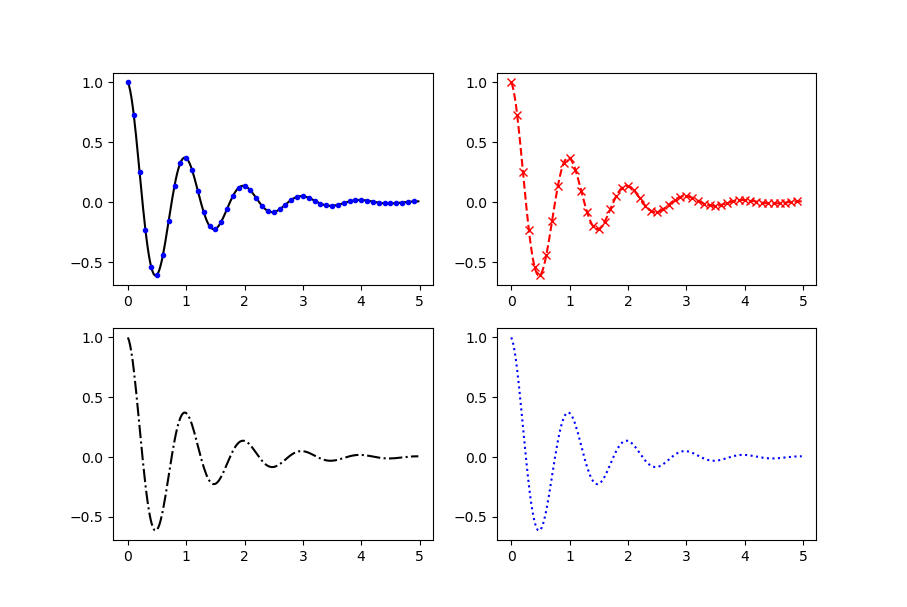
他にもplotメソッドの引数を与えてマーカーの透明度を操作したり、ラベルのフォントを変更できたりします。是非色々遊んでみて下さい。
折れ線&曲線のグラフ
折れ線グラフで点と線の色を変えたいときは別々に描画するか、括弧内に「$x$座標, $y$座標, 書式」の順に2回書きます。
import numpy as np import matplotlib.pyplot as plt x = np.random.rand(40) xc = np.array(range(40))/40 plt.plot(xc, xc**2+1/(x+2), 'r-', xc, xc**2+1/(x+2), 'k.') plt.show()

曲線のグラフは定義域内に多数の点を取って線を結ぶという方法で描画します。そのため、$x$座標の配列を用意する必要があります。以下の例では np.arange(0.0, 5.0, 0.02) として$0$~$5$までの区間に$0.02$の間隔で$250$個の点を生成して描画しています。
import numpy as np
import matplotlib.pyplot as plt
def f(t):
return np.exp(-t) * np.cos(2*np.pi*t)
x = np.arange(0.0, 5.0, 0.02)
plt.plot(x, f(x), 'b:')
plt.show()
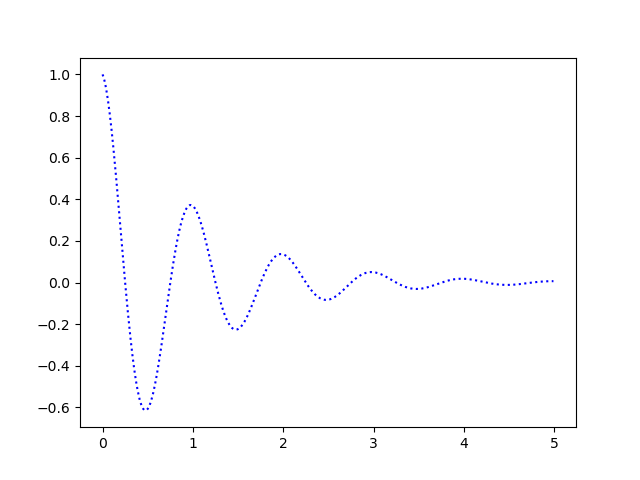
画素数や曲線の曲率にも依りますが、$f(x)=e^{-x}\cos 2\pi x$ 程度なら$250$点も取れば十分滑らかに見えます。$100$点くらいだとカーブがやや角ばりますが、何万点もサンプリングする必要はありません。丁度良い塩梅になるように適宜調整しましょう。
棒グラフ
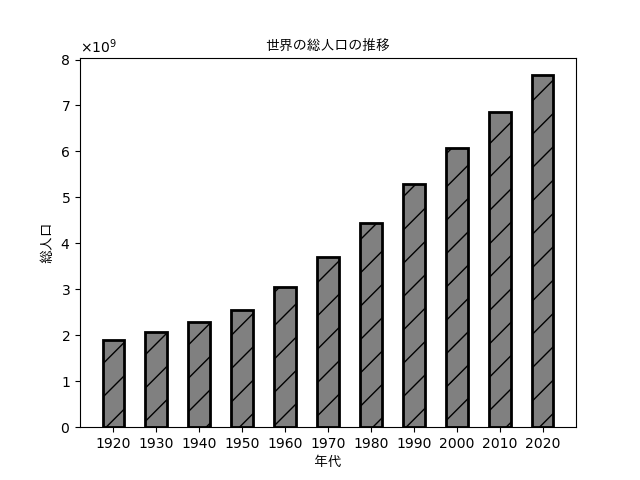
以下は、1920年から2020年にかけての世界の総人口の推移を棒グラフで出力するコードです。日本語を表示するためにごちゃごちゃやっていますが、本質部分はbar()関数です。widthは棒の幅、colorは塗りつぶし色、edgecolorは枠線の塗りつぶし色、linewidthは棒の枠線の太さ、tick_labelは横軸のラベル、hatchは棒の模様を指定するパラメータです。
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties # フォントに関するモジュール
from matplotlib.ticker import ScalarFormatter # 軸フォーマットに関するモジュール
fp = FontProperties(fname='ttfファイルのパス') # パスはご自分で指定して下さい
left = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
height = [1888034127, 2073363421, 2299541939, 2555948654, 3041593413, 3711800786, 4452766336, 5282371928, 6084907596, 6866880431, 7659291953]
labels = ['1920', '1930', '1940', '1950', '1960', '1970', '1980', '1990', '2000', '2010', '2020']
fig = plt.figure()
ax = fig.add_subplot(111)
ax.bar(left, height, width=0.5, color='0.5',
edgecolor='k', linewidth=2, tick_label=labels, hatch='/')
ax.yaxis.set_major_formatter(ScalarFormatter(useMathText=True)) # 縦軸を指数形式に
plt.title("世界の総人口の推移",fontproperties=fp) # fontpropertiesでフォントを指定
plt.xlabel("年代",fontproperties=fp)
plt.ylabel("総人口",fontproperties=fp)
plt.show()
※ttfファイルのパスはWindowsの場合、C:/Users/ユーザー名/AppData/Local/Microsoft/Windows/Fonts/何とか.ttf などと与えます。ttfファイル自体はネット上で様々なものが配布されています。
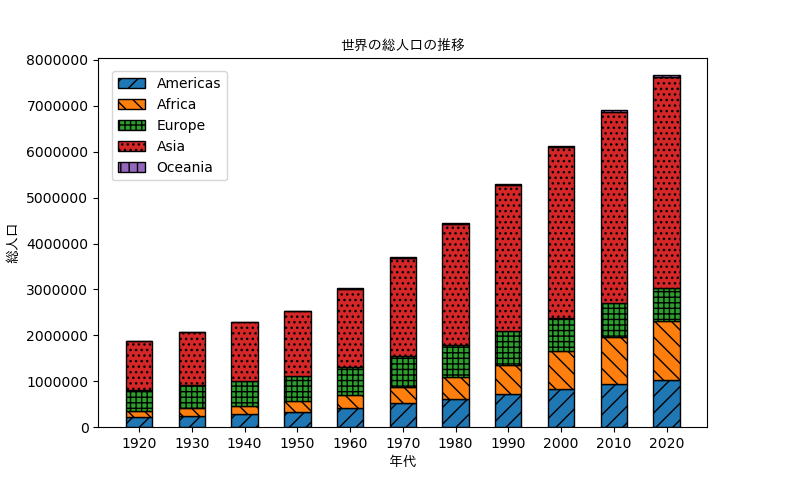
積み上げ棒グラフ(Stacked barplot)を描くのはやや複雑です。
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties # フォントに関するモジュール
import numpy as np
fp = FontProperties(fname='ttfファイルのパス') # パスはご自分で指定して下さい
left = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
pop = np.array([[212014, 252980, 278333, 339241, 424317, 519475, 619925, 728191, 838720, 942271, 1038832],
[143169, 165022, 191640, 224202, 282241, 364132, 479786, 637421, 820959, 1032013, 1270528],
[465506, 501094, 545042, 548194, 605201, 656666, 693170, 721322, 728501, 730478, 722060],
[1060252, 1145914, 1275043, 1410649, 1704289, 2138765, 2635738, 3181211, 3704838, 4166308, 4596189],
[7090, 8349, 9481, 12807, 15884, 19639, 22852, 26733, 31106, 35489, 39482]])
labels = ['1920', '1930', '1940', '1950', '1960', '1970', '1980', '1990', '2000', '2010', '2020']
hatch_list = ['//', '\\\\', '+++', '...', '||']
fig = plt.figure()
ax = fig.add_subplot(111)
for i in range(pop.shape[0]):
plt.bar(left, pop[i],
bottom = np.sum(pop[:i], axis = 0),
width=0.5, edgecolor='k', linewidth=1,
tick_label=labels, hatch=hatch_list[i % len(hatch_list)])
plt.title("世界の総人口の推移",fontproperties=fp)
plt.xlabel("年代",fontproperties=fp)
plt.ylabel("総人口",fontproperties=fp)
ax.legend(["Americas", "Africa", "Europe", "Asia", "Oceania"], loc='upper left', borderaxespad=1)
plt.show()
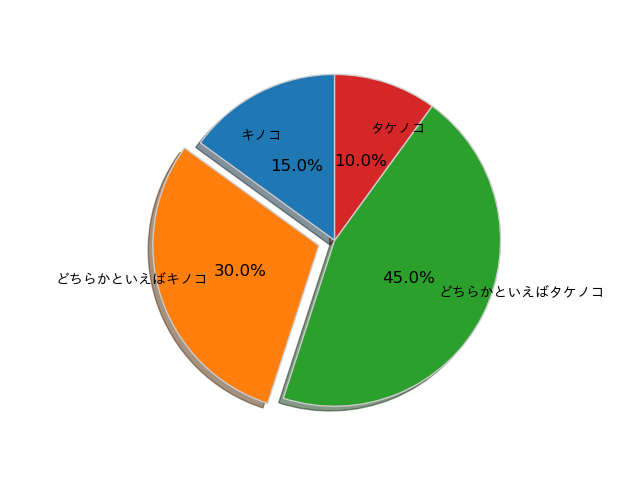
円グラフ
円グラフの描画は次のようにします。pie()関数は引数が多く、使いこなすのが難しいかもしれません。ここで、plt.pieは (patches, texts, autotexts)のタプルを返します。textsがlabalデータなので、この変数にフォントを割り当てています。
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties # フォントに関するモジュール
import numpy as np fp = FontProperties(fname='ttfファイルのパス') # パスはご自分で指定して下さい
labels = ['キノコ', 'どちらかといえばキノコ', 'どちらかといえばタケノコ', 'タケノコ']
sizes = [15, 30, 45, 10]
explode = [0, 0.1, 0, 0]
fig, ax = plt.subplots()
patches, texts, autotexts = ax.pie(sizes, explode=explode, labels=labels, autopct='%1.1f%%',
shadow=True, startangle=90, labeldistance=0.7, pctdistance=0.5, wedgeprops={'linewidth': 1, 'edgecolor':"0.8"})
ax.axis('equal') # 面積比=割合
plt.setp(autotexts, size=12)
plt.setp(texts, fontproperties=fp)
plt.show()
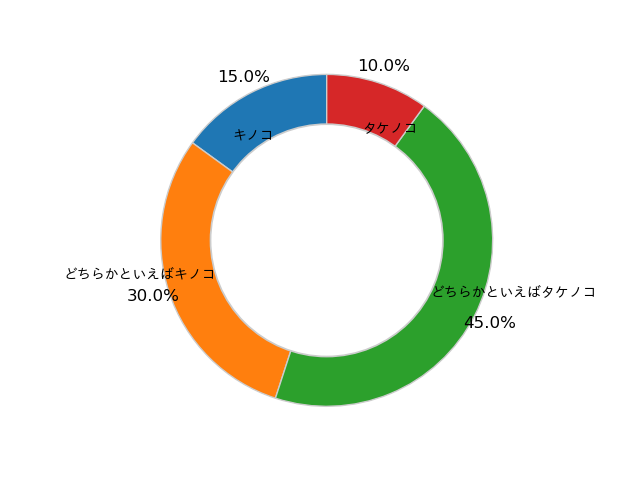
中央に新たな円を追加すればドーナツ型の円グラフが得られます。
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties # フォントに関するモジュール
import numpy as np fp = FontProperties(fname='ttfファイルのパス') # パスはご自分で指定して下さい
labels = ['キノコ', 'どちらかといえばキノコ', 'どちらかといえばタケノコ', 'タケノコ']
sizes = [15, 30, 45, 10]
fig, ax = plt.subplots()
patches, texts, autotexts = ax.pie(sizes, labels=labels, autopct='%1.1f%%',
startangle=90, labeldistance=0.7, pctdistance=1.1, wedgeprops={'linewidth': 1, 'edgecolor':"0.8"})
ax.axis('equal') # 面積比=割合
plt.setp(autotexts, size=12)
plt.setp(texts, fontproperties=fp)
centre_circle = plt.Circle((0, 0), 0.7, color='0.8', fc='white', linewidth=1.25)
fig = plt.gcf()
fig.gca().add_artist(centre_circle)
plt.show()
ヒストグラム
サイコロを$10$回振って出た目の総和を横軸とし、総和の値が現れた回数を縦軸にとった分布を以下に示します。累積値が多いほど縦軸が伸びます。このようなグラフをヒストグラムと呼びます。
import numpy as np
import matplotlib.pyplot as plt
list = []
for _ in range(10000):
list.append(np.random.randint(1, 7, size=10).sum())
plt.hist(list, 20, color="b", rwidth=0.8)
plt.show()
rwidthは棒の画像的な幅を指定する値で、デフォルトでは$1$です。binsは棒の数値的な幅(積算する範囲)を指定する値です。
この例に関して言えば、rangeの値を大きくして試行回数を増やすと(乱数が一様にランダムに生成される限り)二項分布が正規分布に近づく様子を観察することができます。
散布図とカラーバー
scatter()関数で散布図が描けます。scatter()関数には幾つか引数を与えることができ、sで点の大きさを、cで色を、alphaで透明度を指定できます。
import numpy as np import matplotlib.pyplot as plt x = np.random.randn(200) y = np.random.randn(200) fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(x, y, s=100, c='r', alpha=0.3) plt.show()
散布図に複数のプロットを描くこともできます。
import numpy as np
import matplotlib.pyplot as plt
x = np.random.randn(200)
y = np.random.randn(200)
fig = plt.figure()
ax = fig.add_subplot(111)
plt.title("scatter plot")
plt.xlabel("x axis")
plt.ylabel("y axis")
ax.scatter(x, y, s=100, c='r', alpha=0.3)
ax.scatter(y, x**2, s=100, c='b', alpha=0.3)
plt.show()
重ね描きすれば以下のように幾らでもプロットの種類を増やせますが、分かりやすくするために凡例を付けるべきですね。
プロットする点の大きさや色はデータの値に応じて変えることができます。入力データが第$3$軸方向の値を持つ場合はカラーバーを併記して出力することをお勧めします。
import numpy as np import matplotlib.pyplot as plt x = np.random.randn(200) y = np.random.randn(200) z = np.sin(x+y) fig = plt.figure() ax = fig.add_subplot(111) ax_cmap = ax.scatter(x, y, s=50+100*z**2, c=z, cmap='viridis', alpha=0.3) fig.colorbar(ax_cmap) plt.show()
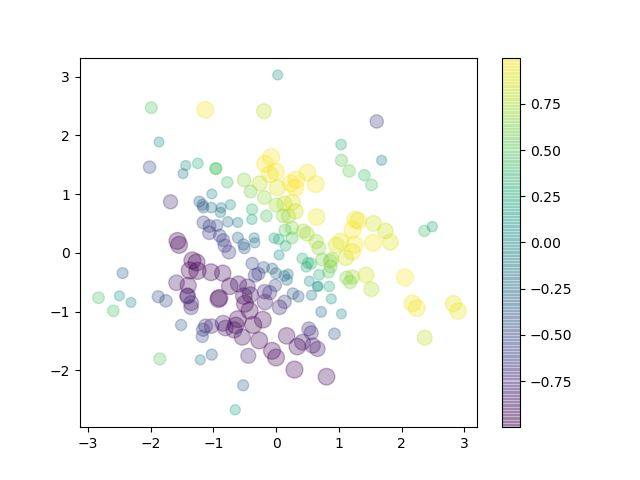
上図ではカラーマップのパラメータを cmap=’viridis’ と指定していますが、他にも “plasma” や “jet”、”gnuplot” などが見やすいと思います。以下にcmapのパラメータ一覧を載せておくので試してみて下さい。
Accent, Accent_r, Blues, Blues_r, BrBG, BrBG_r, BuGn, BuGn_r, BuPu, BuPu_r, CMRmap, CMRmap_r, Dark2, Dark2_r, GnBu, GnBu_r, Greens, Greens_r, Greys, Greys_r, OrRd, OrRd_r, Oranges, Oranges_r, PRGn, PRGn_r, Paired, Paired_r, Pastel1, Pastel1_r, Pastel2, Pastel2_r, PiYG, PiYG_r, PuBu, PuBuGn, PuBuGn_r, PuBu_r, PuOr, PuOr_r, PuRd, PuRd_r, Purples, Purples_r, RdBu, RdBu_r, RdGy, RdGy_r, RdPu, RdPu_r, RdYlBu, RdYlBu_r, RdYlGn, RdYlGn_r, Reds, Reds_r, Set1, Set1_r, Set2, Set2_r, Set3, Set3_r, Spectral, Spectral_r, Wistia, Wistia_r, YlGn, YlGnBu, YlGnBu_r, YlGn_r, YlOrBr, YlOrBr_r, YlOrRd, YlOrRd_r, afmhot, afmhot_r, autumn, autumn_r, binary, binary_r, bone, bone_r, brg, brg_r, bwr, bwr_r, cividis, cividis_r, cool, cool_r, coolwarm, coolwarm_r, copper, copper_r, cubehelix, cubehelix_r, flag, flag_r, gist_earth, gist_earth_r, gist_gray, gist_gray_r, gist_heat, gist_heat_r, gist_ncar, gist_ncar_r, gist_rainbow, gist_rainbow_r, gist_stern, gist_stern_r, gist_yarg, gist_yarg_r, gnuplot, gnuplot2, gnuplot2_r, gnuplot_r, gray, gray_r, hot, hot_r, hsv, hsv_r, inferno, inferno_r, jet, jet_r, magma, magma_r, nipy_spectral, nipy_spectral_r, ocean, ocean_r, pink, pink_r, plasma, plasma_r, prism, prism_r, rainbow, rainbow_r, seismic, seismic_r, spring, spring_r, summer, summer_r, tab10, tab10_r, tab20, tab20_r, tab20b, tab20b_r, tab20c, tab20c_r, terrain, terrain_r, twilight, twilight_r, twilight_shifted, twilight_shifted_r, viridis, viridis_r, winter, winter_r
※これで全部という訳ではないので、ご注意下さい!
(カラーマップの公式ドキュメントはこちら)
ヒートマップ
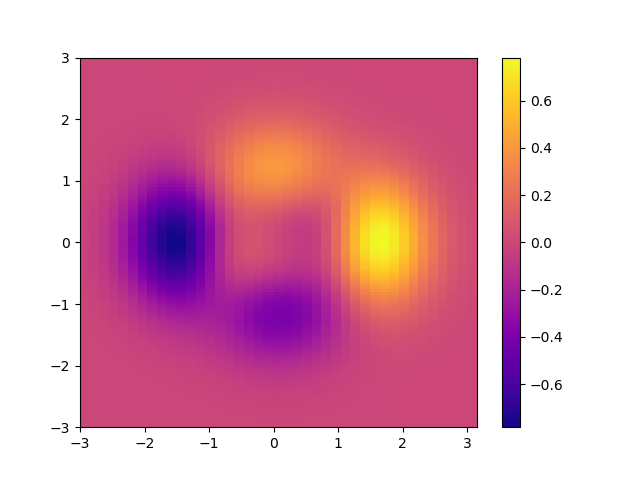
色合いや濃淡で2次元データの個々の値を表示した分布図をヒートマップと呼びます。グリッドを定義するのが面倒ですが、物性値や記述子の相関を調べる上では散布図よりも役立つことが多い表現方法です。
import numpy as np import matplotlib.pyplot as plt dx, dy = 0.15, 0.05 y, x = np.mgrid[slice(-3, 3 + dy, dy), slice(-3, 3 + dx, dx)] z = (- x / 5 + x ** 5 + y ** 3) * np.exp(-x ** 2 - y ** 2) z = z[:-1, :-1] z_min, z_max = -np.abs(z).max(), np.abs(z).max() fig = plt.figure() ax = fig.add_subplot(111) ax_hmap = ax.pcolor(x, y, z, cmap='plasma', vmin=z_min, vmax=z_max) fig.colorbar(ax_hmap) plt.show()
複数の線を表示する
plotメソッドで複数回書き出すことで、複数の曲線を同じ平面上に表示することができます。
import numpy as np
import matplotlib.pyplot as plt
def f(t):
return np.exp(-t) * np.cos(2*np.pi*t)
x = np.arange(0.0, 5.0, 0.02)
plt.plot(x, f(x), 'b:')
plt.plot(x, f(x+0.2), 'r-')
plt.plot(x, f(2*x), 'g--')
plt.show()
等高線&濃淡のある等高線
matplotlibでは等高線をフレキシブルに描画することができます。ここでは例として「Müller-Brownポテンシャル曲面*」を描いてみます。np.linspaceでどのくらい細かくメッシュを定義するかによって等高線の滑らかさが変わります。
import matplotlib.pyplot as plt
import numpy as np
def f(x, y):
A=[-200,-100,-170,15]
a=[-1,-1,-6.5,0.7]
b=[0,0,11,0.6]
c=[-10,-10,-6.5,0.7]
p=[1,0,-0.5,-1]
q=[0,0.5,1.5,1]
s = []
for i in range(4):
s.append(A[i]*np.exp(a[i]*(x-p[i])**2+b[i]*(x-p[i])*(y-q[i])+c[i]*(y-q[i])**2))
return sum(s)
level = []
for i in range(-8,20):
level.append(20*i)
x = np.linspace(-2.0, 1.5, 300)
y = np.linspace(-1.0, 2.5, 300)
xmesh, ymesh = np.meshgrid(x, y)
z = f(xmesh, ymesh)
cont = plt.contour(x, y, z, levels=level)
# cont.clabel(fmt='%1.1f', fontsize=10) # 等高線の数値
plt.show()
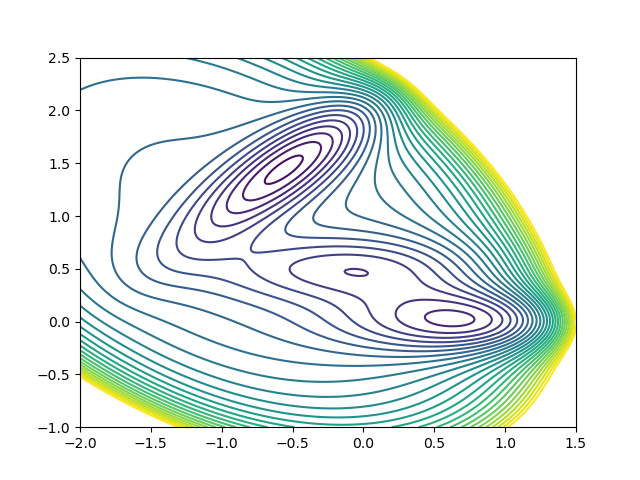
デフォルトだと上図のようなグラデーションになります。等高線の色はcolorsで任意に指定可能ですが、このとき等高線の数に合わせてリスト型で色を指定して下さい。cmapで色調のプリセットを指定しても良いでしょう。
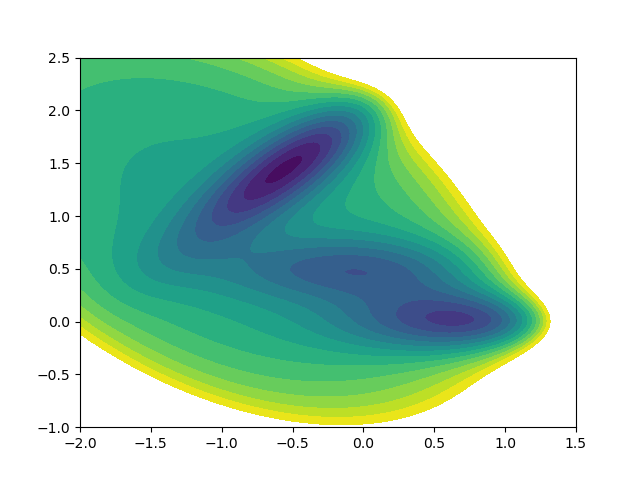
また、領域を塗りつぶすときはcontour関数の代わりにcontourf関数を用います。
import matplotlib.pyplot as plt
import numpy as np
def f(x, y):
A=[-200,-100,-170,15]
a=[-1,-1,-6.5,0.7]
b=[0,0,11,0.6]
c=[-10,-10,-6.5,0.7]
p=[1,0,-0.5,-1]
q=[0,0.5,1.5,1]
s = []
for i in range(4):
s.append(A[i]*np.exp(a[i]*(x-p[i])**2+b[i]*(x-p[i])*(y-q[i])+c[i]*(y-q[i])**2))
return sum(s)
level = []
for i in range(-8,8):
level.append(20*i)
x = np.linspace(-2.0, 1.5, 300)
y = np.linspace(-1.0, 2.5, 300)
xmesh, ymesh = np.meshgrid(x, y)
z = f(xmesh, ymesh)
cont = plt.contourf(x, y, z, levels=level)
plt.show()
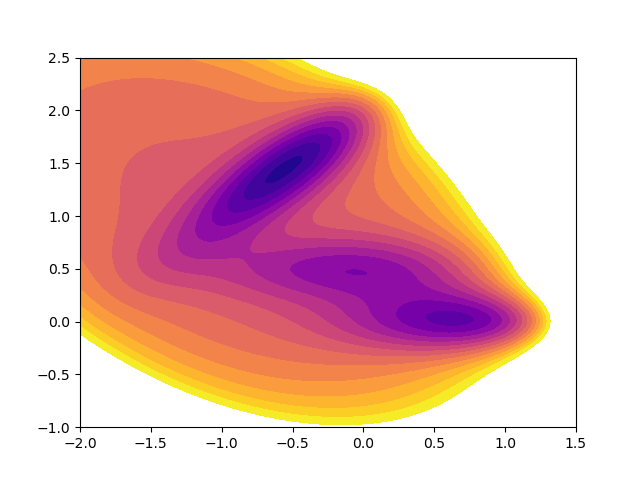
例えば、contourf関数の引数として cmap=’plasma’ を指定すると以下のような色合いになります。
*参考:K. Müller and L. D. Brown, “Location of Saddle Points and Minimum Energy Paths by a Constrained Simplex Optimization Procedure,” Theoretical Chemistry Accounts 1979, 53, 75–93.
3Dのグラフを表示する
mpl_toolkits.mplot3dからAxes3Dをインポートすることで3次元グラフに対応します。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
left = [1, 2, 3, 4, 5]
height = [2, 4, 8, 16, 32]
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.bar(left, height, zs=0, zdir='y')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
メッシュグリッドを定義すれば曲面も描画できます。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
def func1(x, y):
return x**2 + y**2
x = np.arange(-3.0, 3.0, 0.05)
y = np.arange(-3.0, 3.0, 0.05)
X, Y = np.meshgrid(x, y)
Z = func1(X, Y)
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("f(x, y)")
ax.plot_wireframe(X, Y, Z)
plt.show()
3次元散布図も描画できます。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
X = np.array([i for i in range(1,200)])
Y = X * np.sin(X)
Z = X * np.sin(Y)
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
ax.plot(X, Y, Z, marker="o", linestyle='None', alpha=0.5)
plt.show()
頑張ればこんなのも描けます。画像をドラッグorスワイプすれば立体を動かせます。(公式ドキュメントのコードを一部改変しています)
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.colors
import numpy as np
def midpoints(x):
sl = ()
for i in range(x.ndim):
x = (x[sl + np.index_exp[:-1]] + x[sl + np.index_exp[1:]]) / 2.0
sl += np.index_exp[:]
return x
r, theta, z = np.mgrid[0:1:11j, 0:np.pi*2:25j, -0.5:0.5:11j]
x = r*np.cos(theta)
y = r*np.sin(theta)
rc, thetac, zc = midpoints(r), midpoints(theta), midpoints(z)
sphere = (rc - 0.7)**2 + (zc + 0.2*np.cos(thetac*2))**2 < 0.2**2
hsv = np.zeros(sphere.shape + (3,))
hsv[..., 0] = thetac / (np.pi*2)
hsv[..., 1] = rc
hsv[..., 2] = zc + 0.5
colors = matplotlib.colors.hsv_to_rgb(hsv)
fig = plt.figure()
ax = Axes3D(fig)
ax.voxels(x, y, z, sphere,
facecolors=colors,
edgecolors=np.clip(2*colors - 0.5, 0, 1), # brighter
linewidth=0.5)
ax.axis("off")
plt.show()

(mpl_toolkits.mplot3d.axes3d.Axes3Dの公式ドキュメントはこちら)
複数のグラフを並べる
これまで紹介してきたコードにも何度か登場していますが、subplotという関数によってグラフの位置を規定することができます。例えばsubplot(2,2,3)の場合は「$2 \times 2$ の$3$番目の位置」を意味します。基本的にはどのような種類のグラフを載せようとも、位置の割り当て方は同じです。
import numpy as np
import matplotlib.pyplot as plt
def f(t):
return np.exp(-t) * np.cos(2*np.pi*t)
x1 = np.arange(0.0, 5.0, 0.02)
x2 = np.arange(0.0, 5.0, 0.1)
ax1 = plt.subplot(2,2,1)
ax2 = plt.subplot(2,2,2)
ax3 = plt.subplot(2,2,3)
ax4 = plt.subplot(2,2,4)
ax1.plot(x1, f(x1), 'k-', x2, f(x2), 'b.')
ax2.plot(x1, f(x1), 'r--', x2, f(x2), 'rx')
ax3.plot(x1, f(x1), 'k-.')
ax4.plot(x1, f(x1), 'b:')
plt.show()
最後に
グラフが鮮やかであることと読み取りやすさは比例しません。グラフはデータを可視化して効率良く情報を読み取ることを助けますが、場合によってはデータの意味を取り違えてしまったり、情報の本質を見落としてしまうことに繋がったりしかねません。中には意図的にミスリードを誘うようなグラフが作られる悪質な例さえあります。
どのようなデータがどのような種類のグラフによる可視化に向いているのかを知っておくことはmatplotlibを使う以前の事柄であり、グラフに騙されないためにも大切です。グラフが世の中でどのように使われているのかを普段から観察する癖を付けてみましょう。思わぬことがきっかけで効果的な可視化のアイデアが生まれるかもしれません。
ここまで沢山のグラフを示してきましたが、ご覧の通り「matplotlib」は高品質なグラフ描画機能を提供するパッケージであり、Pythonで可視化するならmatplotlib、というのが事実上のスタンダードです。最近話題に上がることの多くなってきたJulia言語でもPyPlotパッケージからmatplotlibを呼び出せます。matplotlibの使い方に慣れておくことは様々なデータを可視化していく上で非常に重要であり、将来ますます使用頻度が高くなることでしょう。今後、皆さんがmatplotlibを使うにあたって、本稿の内容が役立てば幸いです。

 (公式ドキュメントは
(公式ドキュメントは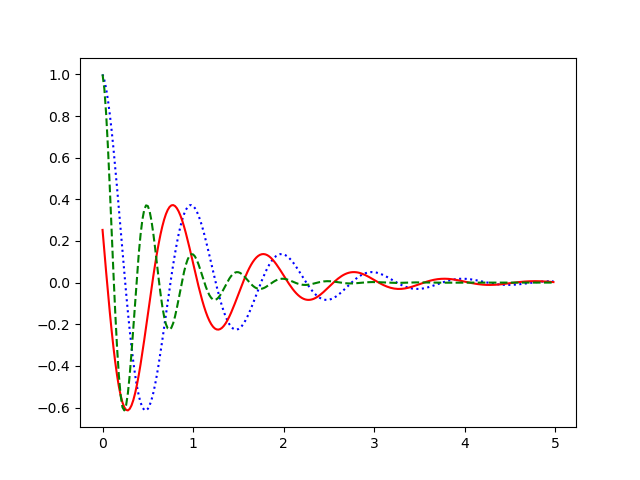
“【Python】matplotlibでグラフを作成する方法【総まとめ】” への1件の返信