Sympyライブラリの添え字付きシンボルを複数個まとめて定義する方法を紹介します。
シンボルの定義
例えば、以下のコードでは
\[\displaystyle \sum_{k=1}^{N} 3^k = \dfrac{3 \left(3^{N}-1\right)}{2}\]
という総和を求める計算が行われます。
import sympy
k, N = sympy.symbols("k N", Integer=True)
f = sympy.summation(3**k, (k, 1, N) )
print(sympy.factor(f))
# 3*(3**N - 1)/2
k, N = sympy.symbols("k N", Integer=True)
という行で $k$、$N$ という2つの文字変数を定義しています。sympy.symbols関数の第2引数の「Integer=True」は「整数値として定義する」というフラグです。
Sympyにおいては、宣言された文字変数はデフォルトでは複素数として認識されます。実数や整数、正の数、正整数の範囲で定義するには以下のようにします。
# 実数
a = sympy.symbols("a", real=True)
# 正の実数
b = sympy.symbols("b", positive=True)
# 整数
c = sympy.symbols("c", Integer=True)
# 正の整数
d = sympy.symbols("d", Integer=True, positive=True)
# 有理数
r = sympy.symbols("r", Rational=True)
複数個のシンボルを一括定義する
複数個のシンボルを一括で定義するには上記のように一つずつ文字を記入するか、以下のようにスライス記法を使います。これは便利なので是非覚えておきたい方法です。
import sympy
chrs = sympy.symbols("a:z", Integer=True)
var = list(chrs)
print(var)
# [a, b, c, ..., x, y, z]
これだけで $a$~$z$ までの26文字の変数が用意できます。$z$を大文字にすれば26個の大文字も一括でシンボルとして定義できます。
添え字を含む文字変数を定義する場合は以下のようにします。
import sympy
chrs = sympy.symbols("a_{0:10}", Integer=True)
var = list(chrs)
print(var)
# [a_{0}, a_{1}, ..., a_{8}, a_{9}]
これだけで $a_{0}$~$a_{9}$ までの10個の変数が一括で定義できます。
波括弧は有っても無くても挙動上の違いはありませんが、LaTeXコマンドとして利用する際には波括弧で添え字が括られていた方が何かと使い勝手が良いと思います。
それに、以下のように添え字が複数ある場合は波括弧が必要になります。
#添え字が複数の場合
import sympy
chrs = sympy.symbols("a_{1:4\,1:4}", real=True)
var = list(chrs)
print(var)
# [a_{1,1}, a_{1,2}, a_{1,3}, a_{2,1}, ..., a_{3,3}]
このコードにより$$\left[ a_{1,1}, \ a_{1,2}, \ a_{1,3}, \ a_{2,1}, \ a_{2,2}, \ a_{2,3}, \ a_{3,1}, \ a_{3,2}, \ a_{3,3}\right]$$という9個の添え字付き文字変数が生成します。ここで、カンマをエスケープしていることに注意しましょう。もしエスケープを忘れると添え字が入れ子になっておかしなことになります。
利用例
一括定義を使うと、例えば、以下のように連分数のLaTeX形式のコードが容易に得られます。
#連分数生成
import sympy
def list_to_frac(l):
expr = 0
for i in reversed(l[1:]):
expr += i
expr = 1/expr
return l[0] + expr
chrs = sympy.symbols("a_{0:10}", Integer=True)
var = list(chrs)
print(sympy.latex(list_to_frac(var)).replace("frac","dfrac"))
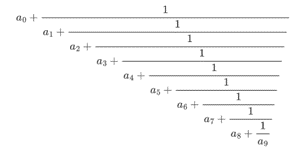
\[\small a_{0} + \dfrac{1}{a_{1} + \dfrac{1}{a_{2} + \dfrac{1}{a_{3} + \dfrac{1}{a_{4} + \dfrac{1}{a_{5} + \dfrac{1}{a_{6} + \dfrac{1}{a_{7} + \dfrac{1}{a_{8} + \dfrac{1}{a_{9}}}}}}}}}}\]
また、一般的な行列の式を書く手間も省けます(ここではnumpyも使っています)。
#3次正方行列生成
import sympy
import numpy
chrs = sympy.symbols("a_{1:4\,1:4}", real=True)
mat_numpy = numpy.array(chrs).reshape(3, 3)
print(mat_numpy)
# [[a_{1,1} a_{1,2} a_{1,3}]
# [a_{2,1} a_{2,2} a_{2,3}]
# [a_{3,1} a_{3,2} a_{3,3}]]
mat_sympy = sympy.Matrix(mat_numpy)
print(mat_sympy)
# Matrix([[a_{1,1}, a_{1,2}, a_{1,3}], [a_{2,1}, a_{2,2}, a_{2,3}], [a_{3,1}, a_{3,2}, a_{3,3}]])
\[\left[\begin{matrix}a_{1,1} & a_{1,2} & a_{1,3}\\a_{2,1} & a_{2,2} & a_{2,3}\\a_{3,1} & a_{3,2} & a_{3,3}\end{matrix}\right]\]
コードを少し改変すれば4次でも5次でもすぐに得られます。
\[\left[\begin{matrix}a_{1,1} & a_{1,2} & a_{1,3} & a_{1,4}\\ a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4}\\ a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4}\\ a_{4,1} & a_{4,2} & a_{4,3} & a_{4,4}\end{matrix}\right]\]
\[\left[\begin{matrix}a_{1,1} & a_{1,2} & a_{1,3} & a_{1,4} & a_{1,5}\\a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4} & a_{2,5}\\a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} & a_{3,5}\\a_{4,1} & a_{4,2} & a_{4,3} & a_{4,4} & a_{4,5}\\a_{5,1} & a_{5,2} & a_{5,3} & a_{5,4} & a_{5,5}\end{matrix}\right]\]
便利ですね!