創作整数問題#13解法＆創作整数問題#14

久々の更新になりました。今回はありふれた話題から。

---

《問題#14》

等式 $p^2+q^2=r^2$ を満たす互いに素な自然数 $p$、$q$、$r$ の組が無数に存在することを示せ。

（創作問題）

---

今回のテーマはピタゴラス数の満たす方程式です。$p$、$q$、$r$ を無数に構成する方法を見つけられればOKです。ちょっとした知識問題かも･･･。

 

 

証明問題なので解答は次回掲載します。

---

創作整数問題#13（解き方）

---

問題#13は素数を含むディオファントス方程式の話題でした。

等式 $p + q = (p − q)^3$を満たす素数 $p$、$q$ の組をすべて求めよ。

結果的には $p+q \pmod{3}$と$(p − q)^3 \pmod{3}$ を調べればよいのですが、まずは偶奇で絞り込んでみましょう。式の形より明らかに $p>q$ ですから、$p、q$がともに偶数となることはありません。したがって偶数が含まれるとしたら $q=2$ の場合のみですが、このとき方程式は$$p^3-6p^2+11p-10=0$$となり、これは整数解を持ちません。よって$p、q$はともに奇数であることが必要ですが、$p=2m+1$、$q=2n+1$ と置いても状況はあまり進展しません。そこで別のアプローチを考えます。そこで$p、q$はともに素数であるという条件を利用して$3$で割った余りによって絞り込んでみましょう。左辺 $p+q$ の$3$で割った余りは以下のようになります。

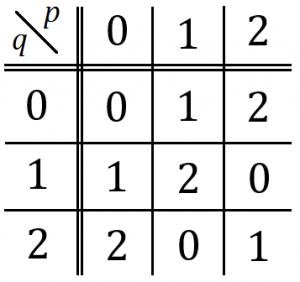
また、右辺 $(p-q)^3$ の$3$で割った余りは以下のようになります。

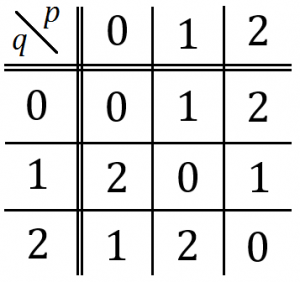
それぞれを比較すると $q \equiv 0 \pmod{3}$ が必要であることが分かります。つまり素数$q$は$3$の倍数でなければならないので、$q=3$ と定まります。これより与式は$$p+3=(p-3)^3$$となります。ここでオーダーに着目すると、$p \geqq 7$ のとき $(p-3)^3>p+3$ となるので $p \leqq 5$ でなければなりません。よって $p=5$ と決まります。

したがって求める組は$$\color{red}{(p,\,q)=(5,\,3)}$$となります。

---

（コメント）

素数を含むディオファントス方程式としては標準的なレベルでしょうか？

こういう問題を処理する際に $\text{mod} \ 3$ が有用だということは記憶に値します。このタイプの問題は京大辺りで頻出ですが、最近は学習指導要領が改訂されたためか、様々な大学で整数問題が出題されやすくなってきています。九州大や千葉大ではこうしたシンプルなディオファントス方程式が出題されやすい傾向にある気がします。

---

（2018/12/16追記）

HN しゅーじ さんより、$\text{mod}\ p+q$ を利用する別解を頂きました。

$\text{mod}\ p+q$ で考えると、$$\begin{align} p-q &\equiv p-q+(p+q) \pmod{p+q} \\ &=2p \end{align}$$より、$$\begin{align} (p-q)^3 &\equiv (2p)^3 \pmod{p+q} \\ &=8p^3 \end{align}$$となります。与式より、$$8p^3 \equiv 0 \pmod{p+q}\tag*{(★)}$$が成り立ちますが、与式より明らかに $p>q$ なので $p \ne q$ です。よって $p+q$ と $p$ は互いに素であり、$p+q$ が $p^3$ を割り切ることはないので、$(★)$式が成り立つためには $p+q$ が $8$ を割り切ることが必要です。そのような素数 $p$、$q$ の組は$$\color{red}{(p,\,q)=(5,\,3)}$$に限るので、これが求める解となります。

この方法だと $\text{mod}\ 3$ を利用するよりも簡潔な解答になります。別解のご提供に感謝致します！