「順像法と逆像法」の解説記事第4弾です。前回同様に今回も線分が通過する領域を扱いますが、今回は場合分けがやや面倒なタイプの問題とその処理方法を紹介します!
※「このサイトを離れますか」や「このサイトを再読み込みしますか」などの警告メッセージが出ることがありますが、これは3Dグラフの表示に利用している geogebra の仕様なので無視して下さい。
《問題》
座標平面上の2点 $\mathrm{P}(t,\,t^{2})$、$\mathrm{Q}(t-5,\,t^{2}-4 t+2)$に対して $t$ が $1 \leqq t \leqq 3$ の範囲を動くとき、以下の各問いに答えよ。
問1 線分$\mathrm{PQ}$を表す直線の方程式および定義域を、$t$を用いて表せ(答えのみでよい)。
問2 線分$\mathrm{PQ}$が通過する範囲 $D$ を求め、図示せよ。
(日本医科大学2016年 第3問)
《考え方》
本問には誘導設問が付いていますが、前回の問題設定とは異なり点$\mathrm{P}$、$\mathrm{Q}$の動きが掴みにくいので図形的な考察に頼るのは難しそうです。ただ、$\mathrm{P}$、$\mathrm{Q}$の座標が与えられているので、直線$\mathrm{PQ}$の方程式を得るのは容易ですね。その後は順像法でも逆像法でも解答可能なので、両方の方針で解き比べてみます。
順像法の場合はパラメータである $t$ の取り得る値の範囲に注意しなければならず、軸と変域の兼ね合いに関する場合分けが少々厄介です(※この部分が本問を取り上げたポイントでもあります!)。初見だと何をやっているのか分かりにくいと思いますので、後ほど分かりやすく説明します。
逆像法の場合は、二次関数の解の配置問題に帰着されます。適切に場合分けできるのであれば、こちらの方針の方がスッキリ解決できるかもしれません。
順像法による解答例
問1
(※答えのみでよい、と指示されていますが、ここでは導出過程の解説も含めて書きます)
$\mathrm{P}(t,\,t^{2})$、$\mathrm{Q}(t-5,\,t^{2}-4 t+2)$を結ぶ直線$\mathrm{PQ}$の傾きは、$$\dfrac{t^{2}-\left(t^{2}-4 t+2\right)}{t-(t-5)}=\dfrac{4 t-2}{5}$$である。これより直線$\mathrm{PQ}$の方程式は、$$y=\dfrac{4 t-2}{5}(x-t)+t^{2}$$ $$\therefore \textcolor{red}{y=\dfrac{4 t-2}{5}x+\dfrac{t^2+2t}{5}}$$となる。また、$t-5<t$ を踏まえると定義域は$$\textcolor{red}{t-5 \leqq x \leqq t}$$となる。
問2
問1の結果より、$t$の取り得る値の範囲は$$\begin{cases}
x \leqq t \leqq x+5 \\
\quad \text{かつ} \\
1 \leqq t \leqq 3
\end{cases}$$となる。
$f(t)=\dfrac{4 t-2}{5}s+\dfrac{t^2+2t}{5}$ と置くと、$$\small \begin{aligned}
y &=f(t) \\
&=\frac{1}{5}\left\{t^{2}+2(2 x+1) t-2 x\right\} \\
&=\frac{1}{5}(t+2 x+1)^{2}-\frac{1}{5}\left(4 x^{2}+6 x+1\right)
\end{aligned}$$と変形できる。これは直線 $t=-2 x-1$ 上に軸が存在する下に凸な放物線の方程式である。
そこで、$x=s$($s$は $-4 \leqq s \leqq 3$ を満たす定数)と固定して、$y=f(t)$ の値域を調べる。このとき、$(x,t)$の存在領域は以下のようになっている。
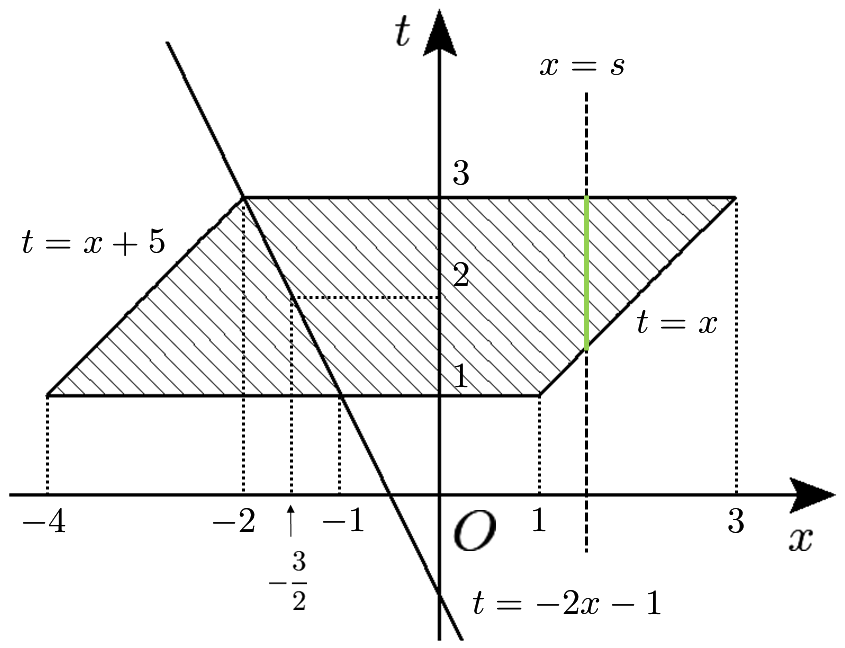
(ⅰ)$-4 \leqq s \leqq -2$ のとき、軸との関係から、$y$の取り得る値の範囲は$$f(s+5) \leqq y \leqq f(1)$$
(ⅱ)$-2 \leqq s \leqq -\dfrac{3}{2}$ のときは$$f(-2s-1) \leqq y \leqq f(1)$$
(ⅲ)$-\dfrac{3}{2} \leqq s \leqq -1$ のときは$$f(-2s-1) \leqq y \leqq f(3)$$
(ⅳ)$-1 \leqq s \leqq 1$ のときは$$f(1) \leqq y \leqq f(3)$$
(ⅴ)$1 \leqq s \leqq 3$ のときは$$f(s) \leqq y \leqq f(3)$$
いま、$t$にそれぞれの値を代入すると$$\begin{aligned}f(1)& =\frac{1}{5}(2s+3) \\ f(3)& =2s+3 \\ f(s)& =s^{2} \\ f(s+5)& =s^{2}+6s+7 \\ f(-2s-1)& =-\dfrac{1}{5}\left(4s^{2}+6s+1\right) \end{aligned}$$となる。よって、$x=s$ の固定を解除すると、(ⅰ)~(ⅴ)より、線分$\mathrm{PQ}$が通過する範囲 $D$ は次のようになる。ただし、境界線はすべて含む。
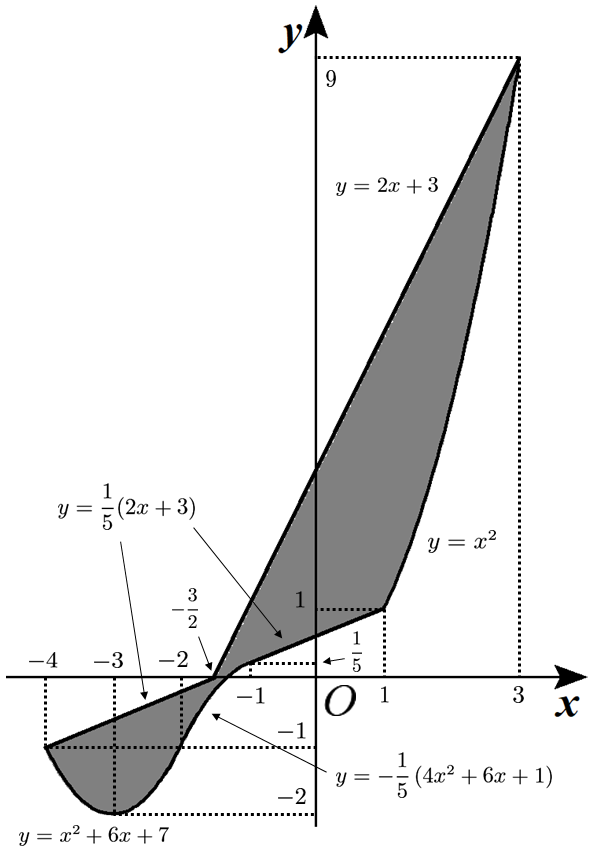
場合分けが複雑でしたね。何をしているのか今一つ分からなかったという方のために、$(x,t)$の存在領域について解説を加えておきます。(以下の説明は特に重要です!)
$(x,t)$の存在領域を改めて図示すると以下のようになります。この図は$(x,t)$の存在領域を真上から見たようなイメージになっており、横軸が$x$軸、縦軸が$t$軸に相当しています。図中のスライドバーで $x=s$ の直線を自由に動かせます。
上図は$xt$平面上に $y=f(t)$ 定義域($(x,t)$の存在領域)を図示したものですが、$y$の値も含めて3次元的に図示すると下図のようになります。
下図中の赤い軸が$x$軸、緑の軸が$t$軸、青い軸が$y$軸にそれぞれ対応します。紫色の領域が定義域($(x,t)$の存在領域)で、黒線は放物線 $y=f(t)$ 軸の軌跡、黄緑色の線は$x$の値を固定したときの曲面の切り口に相当します。
グラフの下の方にあるスライドバー(見当たらない際はスクロールしてください…)でパラメータ$s$の値を色々動かせるので遊んでみて下さい。$s$の値を変えると曲面の切り口の様子も変わるので、なぜ場合分けが5回も必要だったかのが視覚的に理解できると思います。
これを真上方向から見ると、先ほどの平面図と同じ領域に相当しているのが見て取れるはずです。また、$xy$平面に垂直な方向から見ると解答の図そのものになっていることが分かると思います。
※このような曲面は「双曲放物面」(hyperbolic paraboloid) と呼ばれます。これを垂直面(この場合は$xt$平面に垂直な面)で切ると放物線が現れ、水平面で切ると双曲線が現れます。$u=t+2x+1$、$v=2x+\dfrac{3}{2}$ などと変換すれば方程式からも双曲放物面になっていることが確かめられます。
● ● ●
逆像法を用いた場合の解き方も一応載せておきます。問1は上記の解法と同じなので問2から掲載します。
逆像法による解答例
問2
問1で得られた直線$\mathrm{PQ}$の方程式は$$\small t^{2}+2(2 x+1) t-2 x-5 y=0 \quad \cdots ①$$と変形できる。したがって、線分$\mathrm{PQ}$の通過領域を求めるには、$t$の方程式$①$が$$②:x \leqq t \leqq x+5$$かつ$$③:1 \leqq t \leqq 3$$の範囲で少なくとも一つの実数解を持つような$(x,y)$が存在する条件を調べればよい。
ここで$①$の左辺について$$\small \begin{aligned}
f(t) &=t^{2}+2(2 x+1) t-2 x-5 y \\
&=\{t+(2 x+1)\}^{2}-4 x^{2}-6 x-1-5 y
\end{aligned}$$と置き、以下、$tu$平面上で $u=f(t)$ のグラフを考える。
(ア)方程式$①$が2つの実数解(重解を含む)をもつ場合
$t$が$②$を満たすとき、$$\small ④:\left\{\begin{array}{l}
(\text{軸の}u\text{座標}) \leqq 0 \\
x \leqq (\text{軸の}t\text{座標}) \leqq x+5 \\
f(x) \geqq 0 \\
f(x+5) \geqq 0
\end{array}\right.$$ $$\small \iff \left\{\begin{array}{l}
y \geqq \dfrac{1}{5}\left(-4 x^{2}-6 x-1\right) \\
-2 \leqq x \leqq -\dfrac{1}{3} \\
y \leqq x^{2} \\
y \leqq x^{2}+6 x+7
\end{array}\right.$$が必要である。また、$t$が$③$を満たすとき、$$\small ⑤:\left\{\begin{array}{l}
(\text{軸の}u\text{座標}) \leqq 0 \\
1 \leqq (\text{軸の}t\text{座標}) \leqq 3 \\
f(1) \geqq 0 \\
f(3) \geqq 0
\end{array}\right.$$ $$\small \iff \left\{\begin{array}{l}
y \geqq \dfrac{1}{5}\left(-4 x^{2}-6 x-1\right) \\
-2 \leqq x \leqq -1 \\
y \leqq \dfrac{1}{5}(2x+3) \\
y \leqq 2 x+3
\end{array}\right.$$が必要となる。
(イ)方程式$①$が1つの実数解をもつ場合
$t$が$②$を満たすとき、$$\small ⑥:\left\{\begin{array}{l}
f(x) \geqq 0 \\
f(x+5) \leqq 0
\end{array}\right. \text{ または } \left\{\begin{array}{l}
f(x) \leqq 0 \\
f(x+5) \geqq 0
\end{array}\right.$$ $$\small \iff \left\{\begin{array}{ll}
y \geqq x^{2} \\
y \leqq x^{2}+6 x+7 \end{array}\right. \text{ または }\left\{\begin{array}{l}
y \leqq x^{2} \\
y \geqq x^{2}+6 x+7
\end{array}\right.$$が必要である。また、$t$が$③$を満たすとき、$$\small ⑦:\left\{\begin{array}{l}
f(1) \geqq 0 \\
f(3) \leqq 0
\end{array}\right. \text{ または } \left\{\begin{array}{l}
f(1) \leqq 0 \\
f(3) \geqq 0
\end{array}\right.$$ $$\small \iff \left\{\begin{array}{ll}
y \geqq \dfrac{1}{5}(2x+3) \\
y \leqq 2 x+3 \end{array}\right. \text{ または }\left\{\begin{array}{l}
y \leqq \dfrac{1}{5}(2x+3) \\
y \geqq 2 x+3
\end{array}\right.$$が必要となる。
以上(ア)と(イ)より、$②$のときの必要条件は「$④$または$⑥$」であり、$③$のときの必要条件は「$⑤$または$⑦$」である。いま、$②$かつ$③$でなければならないから、求める$(x,y)$が存在する条件は
「$④$または$⑥$」かつ「$⑤$または$⑦$」
となる。(※図示した結果は省略)
最後の最後で「$②$かつ$③$」という条件を忘れてしまうと、間違った領域が求まってしまいます。逆像法を使う場合は漫然と解答していると条件を取り違えてしまいがちので注意しましょう。
受験指導の世界には「難しい問題は逆像法で解け」とかいう迷言(?)が一部で流布していると耳にしたことがありますが、そんなデタラメを鵜呑みにしてはいけません…。順像法や逆像法などと聞くと高尚な感じに聞こえますが、要するにやっていることは「スキャンする」か「実数解の存在条件に持ち込む」の2パターンだけです。問題に応じて臨機応変に使い分けましょう。
本問は前回の東大の問題とは違い、直線の掃過領域から該当する範囲だけを抜き出す、という処理ができないタイプの問題です。本問のようなパラメータの範囲が一定でない問題を順像法で解くと場合分けがやや煩雑になりますが、方程式の特徴(今回は放物線)に合わせて値域を求めれば良いだけなので、ある意味ではパターン問題とも言えます。勿論、実数解の存在条件に持ち込んでもOKですが、順像法で解く方がシンプルなのでおすすめです。
今回の記事では$x$軸と$y$軸に加え、パラメータである$t$の軸も含めた、3次元空間に領域をプロットして説明してみました。こうした解説は紙の参考書ではなかなか難しいと思います。通過領域を求める問題って今までは何だかよく分からなかったけど、実はこういう仕組みで解けていたんだなあ、・・・と思って頂ければ、ここまで連日解説してきた甲斐があったというものです(笑)。
さて、軸の位置で場合分けが必要な問題の類題としては、1984年の京都大学理系第3問や、2007年の東京大学理科第3問、2014年の名古屋大学理系第2問などがあります。1997年の東大文科第4問は直線のパラメータが3次なので順像法が順当な手筋となりますが、微分を使えば逆像法でも解けます。
次回は皆さんお待ちかねの「順像法と逆像法のどちらを選ぶべきか」という内容で、この「順像法と逆像法」を締め括りたいと思います!

“【順像法と逆像法④】線分の掃過領域(日本医科大学2016年)” への2件の返信