今年の阪大の整数問題は４次式を題材にした良問でした。
《問題》
$a$、$b$を正の実数とし、$f(x)=x^4-ax^3+bx^2-ax+1$ とする。
（１）$c$ を実数とし、$f(x)$ が $x-c$ で割り切れるとする。このとき、$c>0$ であり、$f(x)$ は $(x-c)\left(x-\dfrac{1}{c}\right)$ で割り切れることを示せ。
（２）$f(x)$ がある実数 $s$、$t$、$u$、$v$ を用いて$$f(x)=(x-s)(x-t)(x-u)(x-v)$$と因数分解できるとき、$a \geqq 4$ が成り立つことを示せ。
（３）$a=5$ とする。$f(x)$ がある実数 $s$、$t$、$u$、$v$ を用いて$$f(x)=(x-s)(x-t)(x-u)(x-v)$$と因数分解できるような自然数$b$の値をすべて求めよ。
（大阪大学2018年理系 第２問）
《考え方》
（１）
因数定理を利用します。多項式$f(x)$が $x-c$ で割り切れる（因数にもつ）ことは $f(c)=0$ と同値である、というのが因数定理の主張です。$$\small f(c)=c^4-ac^3+bc^2-ac+1$$ですから、$$\small c^4-ac^3+bc^2-ac+1=0 \tag{1.1}$$が条件として得られます。ここで$f\left(\dfrac{1}{c}\right)$を計算してみますと、$$\small \begin{align}f\left(\dfrac{1}{c}\right) &=\dfrac{1}{c^4}-\dfrac{a}{c^3}+\dfrac{b}{c^2}-\dfrac{a}{c}+1 \\ &=\dfrac{1}{c^4}(c^4-ac^3+bc^2-ac+1) \\ &=0 \ \ \ (\because (1.1)) \end{align}$$となります。これより、$f(x)$ が $x-c$ で割り切れるとき、$x-\dfrac{1}{c}$ でも割り切れることが言えました。
これより、$f(x)$は$(x-c)\left(x-\dfrac{1}{c}\right)$で割り切れる･･･と言いたいところですが、$c$と$\dfrac{1}{c}$の値によっては$f(x)$が$(x-c)\left(x-\dfrac{1}{c}\right)$を因数にもたないかもしれません。特に気になるのが $c=1$ のときで、このとき$(x-c)\left(x-\dfrac{1}{c}\right)$は即ち$(x-1)^2$であり、同じ因数を２つもちうることの説明を省いて直ちに証明完了としてしまうと、場合によっては論理の飛躍と受け取られかねません。ここでは $c=1$ のときに$f(x)$が$(x-1)^2$を因数にもつことを示しておきます。
$c=1$ のとき、$$\small f(c)=f(1)=b-2a+2$$より、$$\small b-2a+2=0$$ $$\small \therefore b=2a-2$$となります。これより$f(x)$は、$$\small \begin{align}f(x) &=x^4-ax^3+(2a-2)x^2-ax+1 \\ &=(x^2-1)^2-ax(x-1)^2 \\ &=(x-1)^2\{(x+1)^2-ax\} \end{align}$$と因数分解できるので、$(x-1)^2$で割り切れることが示されました。
もう一つの示すべき条件 $c>0$ ですが、これは$(1.1)$式から示すことができます。$(1.1)$式より、$$c^4+bc^2+1=c \cdot a(c^2+1)$$と式変形できて、左辺が正、右辺の $a(c^2+1)$ も正なので、$c$も正でなければなりません。よって示されました。
● ● ●
（２）
（１）で示した事実から、$f(x)$ がある実数 $s$、$t$、$u$、$v$ を用いて$$\small f(x)=(x-s)(x-t)(x-u)(x-v)$$と因数分解できるのであれば、$$\small u=\dfrac{1}{s}、v=\dfrac{1}{t} \tag{1.2}$$と置けることが分かります）。これは定数項が$1$であることから導かれます（詳しくはコメント欄を参照してください）。
よって解と係数の関係より、$$\small \begin{cases} s+\dfrac{1}{s}+t+\dfrac{1}{t} &=a &\cdots \text{①} \\ st+1+\dfrac{s}{t}+\dfrac{t}{s}+1+\dfrac{1}{st} &= b &\cdots \text{②}\\ t+s+\dfrac{1}{t}+\dfrac{1}{s} &=a &\cdots \text{③} \\ 1 &= 1 &\cdots \text{④} \end{cases}$$が成立します。（※$(1.2)$の関係式により$\text{③}$と$\text{④}$から新しく得られる情報はありませんが、解と係数の関係の分かりやすさのために敢えて書き下しています）
これを見れば、使うべき式は$\text{①}$であるとすぐに気付けると思います。あからさまに相加相乗平均の不等式に持ち込める形になっていますよね？
$s$、$\dfrac{1}{s}$、$t$、$\dfrac{1}{t}$はいずれも正の実数なので相加相乗平均の不等式が利用できて、これより①の左辺について$$\small s+\dfrac{1}{s}+t+\dfrac{1}{t} \geqq 2\sqrt{s \cdot \dfrac{1}{s}+t \cdot \dfrac{1}{t}}=4$$となります。等号成立は$$s=t=1$$のときであり、これによって$$a \geqq 4$$の成立が示されました。
● ● ●
（３）
（３）では文字の置き換え方で計算量がそれなりに変わってきます。最も簡単に計算を進められるのは$$\small S=s+\dfrac{1}{s}、T=t+\dfrac{1}{t}$$という置き換えでしょう。いま $a=5$ なので、これより、$$\small \begin{cases} S+T &=5 &\cdots \text{⑤} \\ ST+2 &= b &\cdots \text{⑥} \end{cases}$$となります。相加相乗平均の不等式より、$S \geqq 2$、$T \geqq 2$ が成り立っていますので、$\text{⑤}$より、$$\small 2 \leqq S \leqq 3$$が変域として得られます。$\text{⑤}$、$\text{⑥}$より、$$\small S(5-S)+2=b$$ $$\small \therefore -\left(S-\dfrac{5}{2}\right)^2+\dfrac{33}{4}=b \tag{1.3}$$となります。この左辺は図示すると以下のようになるので、可能な自然数$b$は$$b=\color{red}{8}$$ と求められます。このとき、確かに$$\small f(x)=(x-1)^2 \left(x-\dfrac{3+\sqrt{5}}{2}\right)\left(x-\dfrac{3-\sqrt{5}}{2}\right)$$となるので適しています。
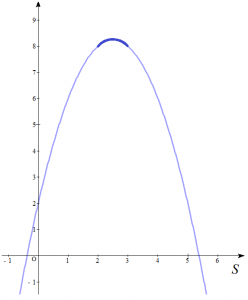（青色太線部が$(1.3)$の左辺を図示したもの）
(2018/03/12)
当サイトがいつもお世話になっている たけちゃん さんから（３）の別解を頂きました。
|
» 別解（たけちゃん さん提供） 《（３）の別解（たけちゃん さん提供）》 $a=5$ のとき，$$f(x)=(x^2+1)^2-5x(x^2+1)+(b-2)x^2$$すなわち さて，(1)の結果から，$f(x)$ がある実数 $s,\ t,\ u,\ v$ を用いて$$f(x)=(x-s)(x-t)(x-u)(x-v)$$と因数分解できるとき，$s,\ t,\ u,\ v$ はすべて正であり，また，((2)とも共通に，$s,\ \dfrac{1}{s},\ t,\dfrac{1}{t}$ と決めつけるのは少し危険な気もしますが，)2組の「互いに逆数である2数の組」となるから，$s,\ t,\ u,\ v$ のうちの2つは 1 以下で，残り2つは $1$ 以上．よって，$f(1) \geqq 0$，すなわち $b \geqq 8$ を得る． 以上より，自然数 $b$ は $b=8$ に限る．このとき，$$\begin{align} f(x) &=x^4-5x^3+8x^2-5x+1 \\ &=(x-1)^4-(x^3-2x^2+x) \\ &=(x-1)^2(x^2-3x+1) \end{align}$$であり，$$x^2-3x+1=\left(x-\dfrac{3+\sqrt{5}}{2}\right)\left(x-\dfrac{3-\sqrt{5}}{2}\right)$$であるから条件を満たす．
» 閉じる |
（コメント①）
方程式・多項式についての基礎的な知識を問う良質な問題だったと思います。
（１）ですが、$f'(c)=0$ となることから$f(c)$が$(x-c)^2$を因数としてもつことを示した方もいるかもしれません。実際、$f(c)=f'(c)=0$ であることは$f(c)$が$(x-c)^2$を因数にもつことの必要十分条件なのですが、これを自明のこととして利用して良いか否かという点については議論の余地がありそうなものです。この事実を答案の中で証明するのは、慣れていなければ思いつくのがなかなか難しく、書けるとしても割と時間を取られるため、導関数からのアプローチはあまりおすすめできません。上記のようにそのまま $f(c)=0$ で得られた条件を使って$f(x)$を因数分解してしまうのが最適でしょう。
また、（３）については$$\small S=s+\dfrac{1}{s}、T=t+\dfrac{1}{t}$$という置き換えを利用しましたが、得られている関係式が対称式であることから、$$X=s+t、Y=st$$という置き換えを選択した方もいると思います。この方針でも解けないことはありませんが、絞り込みがかなり厄介だったり、場合によっては $\small Y+\dfrac{1}{Y}+\dfrac{25Y}{(Y+1)^2}$ などの怪しい関数(笑)が出てきたりして結構計算が大変です。どの方針でも共通して目指すべきなのは第一に自然数$b$の絞り込みであり、大雑把でもいいので$b$の範囲をある程度（上から）押さえることができたら、シラミ潰しという整数問題ならではの手段も使えます。上手く絞り込むことも大切ですが、まずは、そもそもどうやったら絞り込みができるのかをよく考えましょう！
（コメント②）
本問で登場した多項式$f(x)$は右から見ても左から見ても係数が同じ、という係数に関して左右対称な多項式です。このような多項式について $f(x)=0$ とした方程式を「相反方程式」または「回文方程式」と言います。本問のような４次の相反方程式は $t=x+\dfrac{1}{x}$ という置き換えによって二次式の積に分解することができます。
今回の $\small x^4-ax^3+bx^2-ax+1=0$ という場合だと、$$\small x^2-ax+b-\dfrac{a}{x}+\dfrac{1}{x^2}=0$$ $$\small \therefore \left(x+\dfrac{1}{x}\right)^2-a\left(x+\dfrac{1}{x}\right)+b-2=0$$ $$\small \therefore t^2-at+b-2=0$$と変形でき、$$\small t=\dfrac{a \pm \sqrt{a^2-4(b-2)}}{2}$$を得ます。実はここから$b$の範囲を絞り込むことができます。$t$は実数なので、$a=5$ のとき、$$\small 5^2-4(b-2) \geqq 0$$ $$\therefore b \leqq \dfrac{33}{4} \ \ \ (b \leqq 8)$$を得ます。これにしたがって$1$～$8$までの自然数を$b$に代入してシラミ潰しに調べるのも一案ですね。
(2018/03/19追記)
今年の横浜市立大の理系数学大問〔Ⅱ〕に相反方程式を題材とした出題がありました。
(2) ですが，「$a\geqq4$ が成り立つことを示せ」は，
「$a$ のとり得る値の範囲が $a\geqq4$ であることを示せ」
とは意味が異なります．
(もし後者の意味であるとすれば，$a=4$ だけでなく，
$a\geqq4$ を満たすすべての実数 $a$ に対して，
「適当な $b$ をとれば $f(x)=(x-s)(x-t)(x-u)(x-v)$ の形に因数分解できる」
ことを示す必要があります．)
ここで示すべき命題は，対偶命題
「$a\dfrac{33}4$ であれば，
任意の実数 $x$ に対して $f(x)>0$ となり，不適．
よって，$b\leqq\dfrac{33}4.$
さて，(1)の結果から，$f(x)$ がある実数 $s,\ t,\ u,\ v$ を用いて
\[f(x)=(x-s)(x-t)(x-u)(x-v)\]
と因数分解できるとき，$s,\ t,\ u,\ v$ はすべて正であり，また，
((2)とも共通に，$s,\ \dfrac1s,\ t,\ \dfrac1t$ と決めつけるのは
少し危険な気もしますが，)
2組の「互いに逆数である2数の組」となるから，
$s,\ t,\ u,\ v$ のうちの2つは $1$ 以下で，残り2つは $1$ 以上．
よって，$f(1)\geqq0$，すなわち
\[b\geqq8\]
を得る．
以上より，自然数 $b$ は $b=8$ に限る．
このとき，
\[f(x)=x^4-5x^3+8x^2-5x+1=(x-1)^4-(x^3-2x^2+x)=(x-1)^2(x^2-3x+1)\]
であり，
$x^2-3x+1=\Big(x-\dfrac{3+\sqrt5}2\Big)\Big(x-\dfrac{3-\sqrt5}2\Big)$
であるから条件を満たす．
なお，(1.3)式の左辺は $-\left(S-\dfrac52\right)^2+\dfrac{33}4$ ですね．
(「2乗」が欠落しています．)
あれれ，私の環境では，前の投稿の
「ここで示すべき命題は，対偶命題」の次の行が変になりました．
(その後，かなり欠落が生じています．)
TeXでミスをしたか，あるいは私の環境だけの問題の可能性もありますが，
念のために，「対偶命題」の次行から(3) の別解までを，
TeXを使わない形で再投稿させていただきます．
読みにくくてすみません．
「a33/4 であれば，
任意の実数 x に対して f(x)>0 となり，不適．
よって，b≦33/4.
さて，(1)の結果から，f(x) がある実数 s,t,u,v を用いて
f(x)=(x-s)(x-t)(x-u)(x-v)
と因数分解できるとき，s,t,u,v はすべて正であり，また，
((2)とも共通に，s,1/s,t,1/t と決めつけるのは少し危険な気もしますが，)
2組の「互いに逆数である2数の組」となるから，
s,t,u,v のうちの2つは 1 以下で，残り2つは 1 以上．
よって，$f(1)≧0，すなわち b≧8 を得る．
以上より，自然数 b は b=8 に限る．
このとき，
f(x)=x^4-5x^3+8x^2-5x+1=(x-1)^4-(x^3-2x^2+x)=(x-1)^2(x^2-3x+1)
であり，
x^2-3x+1=(x-(3+√5)/2)(x-(3-√5)/2)
であるから条件を満たす．
不等号「小なり」が原因のようです．
何度もすみませんが，再々投稿です．
「a(小なり)4 のとき，どんな実数 s,t,u,v に対しても
f(x)=(x-s)(x-t)(x-u)(x-v)
とはならない」
と同じ意味ですね．
すると，「等号を成立させる s,t の存在」を明示しなくても
a≧4 の根拠として不足する点はないと思います．
(3) やや遠回りである気もしますが，別解を提示します．
a=5のとき，f(x)=(x^2+1)^2-5x(x^2+1)+(b-2)x^2
すなわち
f(x)=(x^2+1-(5/2)x)^2+(b-33/4)x^2
なので，b>33/4 であれば，
任意の実数 x に対して f(x)>0 となり，不適．
よって，b≦33/4.
さて，(1)の結果から，f(x) がある実数 s,t,u,v を用いて
f(x)=(x-s)(x-t)(x-u)(x-v)
と因数分解できるとき，s,t,u,v はすべて正であり，また，
((2)とも共通に，s,1/s,t,1/t と決めつけるのは少し危険な気もしますが，)
2組の「互いに逆数である2数の組」となるから，
s,t,u,v のうちの2つは 1 以下で，残り2つは 1 以上．
よって，$f(1)≧0，すなわち b≧8 を得る．
以上より，自然数 b は b=8 に限る．
このとき，
f(x)=x^4-5x^3+8x^2-5x+1=(x-1)^4-(x^3-2x^2+x)=(x-1)^2(x^2-3x+1)
であり，
x^2-3x+1=(x-(3+√5)/2)(x-(3-√5)/2)
であるから条件を満たす．
たけちゃん さん
コメントありがとうございます。
「小なり」記号は環境依存文字の場合、当サイトでは正しく表示されないことがあるようです。お使いのデバイスによっても変わってくるかもしれませんね。
$(1.3)$式の脱字を修正させて頂きました。いつもご指摘ありがとうございます。
（２）の内容ですが、確かに「$f(x)$ がある実数 $s$、$t$、$u$、$v$ を用いて$$f(x)=(x-s)(x-t)(x-u)(x-v)$$と因数分解できるならば、少なくとも $a \geqq 4$ が成り立つ」が題意なので等号成立云々に関しては特に言及しなくても、成立を示すことができますね。その点で記事中の説明は少し的外れに映ってしまったかもしれません･･･(^_^;)。
$a<4$ の場合、これを満たすような正の実数$s$、$t$、$u$、$v$は相加相乗平均の不等式から存在しないことが直ちに言えますね。
拙稿では（３）の最後で十分性の確認を省いていましたが、答案中では（２）の等号成立条件よりも寧ろこれを書いておくべきでした。
なお、$$u=\dfrac{1}{s}、v=\dfrac{1}{t} \tag{1.2}$$と表せることは、例えば以下のようにして示せると思います。これは簡単にでもよいので、答案の中で触れておくのが好ましいでしょう。
《証明》
（１）より、$f(x)$が $x=s$ を解にもつとき、$x=\dfrac{1}{s}$ も同様に解となるから、$t$、$u$、$v$のうちいずれか一つが$\dfrac{1}{s}$に一致する。ここで、一般性を失うことなく $u=\dfrac{1}{s}$ と置ける。このとき解と係数の関係より定数項について$$s \cdot \dfrac{1}{s} \cdot tv=1$$ $$\therefore tv=1$$となるので、これより$$v=\dfrac{1}{t}$$を得る。（１）より、このうちのいずれか２つ以上が等しい場合でも$f(x)$はそれらを重解としてもつため、$f(x)$は $x-s$、$x-t$、$x-u$、$x-v$ のすべてを因数として有する。
《了》
また、別解のご提供に感謝致します。勝手ながら記事中に追加させて頂きました。
最初の式変形は平方完成をモチベーションとしたものだと思いますが、試験場で気付くのは少々難しいかもしれません（そう感じるのは私だけでしょうか(笑)？）。