今年の東大物理の力学分野はブランコに関する出題でした。日常生活に身近な題材ということで物理の良い教材になりそうです。
ブランコの問題
東大の問題(2021年東京大学前期物理第1問)を誘導設問の流れに沿って紹介していきます。問題設定は円運動なのですが、円運動の知識を必要としない珍しい出題です。本問の主眼は「ブランコ」という系の面白さを味わえる小問Ⅲでしょう。本問は東大の力学としては平易なレベルだと言えます。
以下、抜粋した問題文(青字部分)とともに問題の流れを一通り眺めてみます。
小問Ⅰ
ブランコの運動を図1-1に示します。
ブランコの支点を$\mathrm{O}$とする。ブランコに乗っている人を質量$m$の質点とみなし、質点$\mathrm{P}$と呼ぶことにする。支点から水平な地面におろした垂線の足を$\mathrm{G}$とする。ブランコの長さ$\mathrm{OP}$を $\ell$、支点$\mathrm{O}$の高さ$\mathrm{OG}$を $\ell+h$ とする。ブランコの振れ角$\angle\mathrm{GOP}$を$\theta$とし、$\mathrm{OG}$を基準に反時計回りを正にとる。重力加速度の大きさを$g$とする。
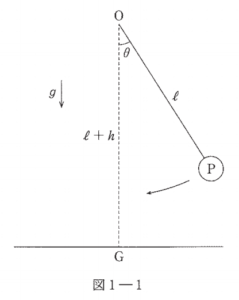
注意点として、ブランコは紙面内のみでたわむことなく運動するものとし、ブランコの質量や摩擦、空気抵抗は無視するものと問題文中で指定されています。
ここまではごく単純な円運動の問題設定です。
質点Pが $\theta = {\theta}_{0}$ から静かに運動を始めるとき、支点$\mathrm{O}$の高さを位置エネルギーの基準とすると、運動を開始した時点における質点Pの力学的エネルギーは $\color{red}{-m g \ell \cos \theta_{0}}$ で与えられます。角度$\theta$における力学的エネルギーは、そのときの質点の速さを$u$とすれば $\color{red}{-m g \ell \cos \theta+\dfrac{1}{2} m u^{2}}$ で与えられるので、カ学的エネルギー保存則から$$u=\color{red}{\sqrt{2 g \ell\left(\cos \theta-\cos \theta_{0}\right)}}$$と表せます。
以上の内容が小問Ⅰで扱われていました。次に小問Ⅱでは二人乗りブランコのモデルが登場します。
小問Ⅱ
質点$\mathrm{A}$、$\mathrm{B}$の質量をそれぞれ$m_\mathrm{A}$、$m_\mathrm{B}$とする。図1-2に示すように、初期状態では$\mathrm{A}$と$\mathrm{B}$が合わさって質点$\mathrm{P}$をなしているとし、質点$\mathrm{P}$が $\theta = {\theta}_{0}$ から静かに運動を始めたとする。$\theta = 0$ において$\mathrm{A}$はブランコを飛び降り、速さ$v_\mathrm{A}$で水平に運動を始めた。一方、$\mathrm{A}$が飛び降りたことにより、$\mathrm{B}$を乗せたブランコは $\theta = 0$ でそのまま静止した。その後$\mathrm{A}$は$\mathrm{G}^{\prime}$に着地した。
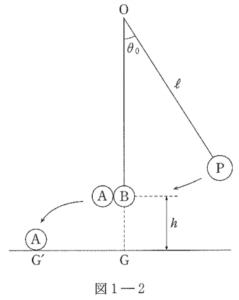
(1)$\mathrm{A}$が飛び降りる直前の質点$\mathrm{P}$の速さを$v$として、$v_\mathrm{A}$を$m_\mathrm{A}$、$m_\mathrm{B}$を用いて表せ。
(2)距離$\mathrm{GG}^{\prime}$を$\ell$、$h$、$\theta_{0}$、$m_{\mathrm{A}}$、$m_{\mathrm{B}}$を用いて表せ。また、$\ell=2.0 \mathrm{~m}$、$h=0.30 \mathrm{~m}$、$\cos \theta_{0}=0.85$、$m_{\mathrm{A}}=m_{\mathrm{B}}$ のとき、距離$\mathrm{GG}^{\prime}$を有効数字2桁で求めよ。
いずれの設問も水平投射と運動量保存則の知識だけで容易に正答を得られます。
$\mathrm{A}$が飛び降りた直後、質点$\mathrm{B}$が静止するから、運動量保存則より$$m_{\mathrm{A}} v_{\mathrm{A}}=\left(m_{\mathrm{A}}+m_{\mathrm{B}}\right) v_{0}$$が成り立ち、ただちに(1)の答え$$v_{\mathrm{A}}=\color{red}{\dfrac{m_{\mathrm{A}}+m_{\mathrm{B}}}{m_{\mathrm{A}}} v_{0}}$$を得ます。(2)は水平投射の運動を水平方向と鉛直方向に分解して考えると良いでしょう。鉛直方向について、$\mathrm{A}$が飛び降りてから着地するまでの時間$t$は$$h=\dfrac{1}{2} g t^{2} \quad \therefore t=\sqrt{\dfrac{2 h}{g}}$$となり、$v_{0}$はⅠで求めた$u$について $\theta=0$ とした場合に相当するので、$$v_{0}=\sqrt{2 g \ell\left(1-\cos \theta_{0}\right)}$$と求められます。水平方向については等速運動なので$$\begin{aligned} \mathrm{GG}^{\prime} &=v_{\mathrm{A}} t \\ &=\left(1+\dfrac{m_{\mathrm{B}}}{m_{\mathrm{A}}}\right) v_{0} t \\ &=\color{red}{2\left(1+\dfrac{m_{\mathrm{B}}}{m_{\mathrm{A}}}\right) \sqrt{h \ell\left(1-\cos \theta_{0}\right)}} \end{aligned}$$となり、$m_{\mathrm{A}}=m_{\mathrm{B}}$ として各数値を代入すると$$\begin{aligned}
\mathrm{GG}^{\prime} &=4 \sqrt{h \ell\left(1-\cos \theta_{0}\right)} \\
&=4 \sqrt{0.30 \times 2.0 \times 0.15} \\
&=4 \times 0.30 \\
&=\color{red}{1.2 \mathrm{~(m)}}
\end{aligned}$$を得ます。
小問Ⅲ
ブランコを漕ぐことを考えよう。ブランコに乗った人が運動の途中で立ち上がったりしゃがみこんだりすることで、ブランコの振れ幅が変化していく。まず図1-3に示すように、人がブランコで一度だけ立ち上がることを以下のように考える。
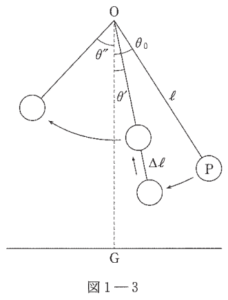
質量$m$の質点$\mathrm{P}$が $\theta=\theta_{0}$($\theta_{0}>0$)から静かに運動を始めた。次に角度 $\theta=\theta^{\prime}$ において人が立ち上がったことにより、$\mathrm{OP}$の長さが $\ell$ から $\ell-\Delta \ell$ へと瞬時に変化したとする($\Delta \ell>0$)。$\mathrm{OP}$の長さが変化する直前の$\mathrm{P}$の速さを$v$とし、直後の速さを$v^{\prime}$とする。その後、$\mathrm{OP}$の長さが $\ell-\Delta \ell$ のまま$\mathrm{P}$は運動を続け、角度 $\theta=-\theta^{\prime \prime}$($\theta^{\prime \prime}>0$)で静止した。ただし以下では、ブランコの振れ角$\theta$は常に十分小さいとして、$\cos \theta \fallingdotseq 1-\dfrac{\theta^{2}}{2}$ と近似できることを用いよ。
$(\theta^{\prime \prime})^2$の式は以下のように求められます。
人がブランコで一度だけ立ち上がった直後と、その後に静止するタイミングについて、力学的エネルギー保存則より$$\small -m g(\ell-\Delta \ell) \cos \theta^{\prime \prime}=-m g(\ell-\Delta \ell) \cos \theta^{\prime}+\dfrac{1}{2} m\left(v^{\prime}\right)^{2}$$が成り立ちます。ここで余弦$\cos \theta$について所与の近似式を適用すると$$\small -m g(\ell-\Delta \ell)\left(1-\frac{\left(\theta^{\prime \prime}\right)^{2}}{2}\right)=-m g(\ell-\Delta \ell)\left(1-\frac{\left(\theta^{\prime}\right)^{2}}{2}\right)+\frac{1}{2} m\left(v^{\prime}\right)^{2}$$ $$\therefore \quad \left(\theta^{\prime \prime}\right)^{2}=\color{red}{\left(\theta^{\prime}\right)^{2}+\frac{\left(v^{\prime}\right)^{2}}{g(\ell-\Delta \ell)}}$$となります。
ここでさらに問題文中で以下のような近似が追加されます。
$\mathrm{OP}$の長さが変化する前後に関して以下のように考えることができる。長さ$\mathrm{OP}$の変化が十分速ければ、瞬間的に$\mathrm{OP}$方向の強い力が働いたと考えられる。$\mathrm{O}$を中心とした座標系で考えると、このカは中心力なので、面積速度が長さ$\mathrm{OP}$の変化の前後で一定であるとしてよい。つまり、$\dfrac{1}{2}(\ell-\Delta \ell) v^{\prime}=\dfrac{1}{2} \ell v$ が成り立つ。
よって、この面積速度一定の条件から$$v^{\prime}=\dfrac{\ell}{\ell-\Delta \ell} v$$となるので、両辺を二乗して$$\begin{aligned} \therefore {v^{\prime}}^{2} &=\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{2} v^{2} \\ &=\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{2} g \ell\left\{{\theta_{0}}^{2}-\left(\theta^{\prime}\right)^{2}\right\} \end{aligned}$$を得ます。途中で近似した結果$$\begin{aligned} v^{2}&=2 g \ell\left(\cos \theta^{\prime}-\cos \theta_{0}\right) \\ & \approx g \ell\left\{\theta_{0}^{2}-\left(\theta^{\prime}\right)^{2}\right\} \end{aligned}$$を用いています。これは小問Ⅰの$u$の式に $\theta=\theta^{\prime}$ を代入したものです。
これを先ほどの$\left(\theta^{\prime \prime}\right)^{2}$の結果に代入して$$\begin{aligned} \left(\theta^{\prime \prime}\right)^{2} &=\left(\theta^{\prime}\right)^{2}+\dfrac{\left(v^{\prime}\right)^{2}}{g(\ell-\Delta \ell)} \\
&=\color{red}{\left(\theta^{\prime}\right)^{2}+\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{3}\left\{\theta_{0}^{2}-\left(\theta^{\prime}\right)^{2}\right\}}\end{aligned}$$を得ます。これは$$\small \left(\theta^{\prime \prime}\right)^{2}=-\left\{\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{3}-1\right\}\left(\theta^{\prime}\right)^{2}+\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{3} \theta_{0}^{2}$$と整理できるので、$\left(\theta^{\prime}\right)^{2}$の係数が負であることを考えると、$\theta^{\prime \prime}$は $\theta^{\prime}=0$ で最大値 $\theta^{\prime \prime}_{\text{max}}=\color{red}{\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{\frac{3}{2}} \theta_{0}}$ を取ることが分かります。
このモデルの結果から何が言えるかというと、ブランコを漕いだときの最高点をできるだけ高くするには、最下点で一気に重心を高くすればよいということです。つまり $\theta^{\prime}=0$ がブランコを漕ぐのに「最適な位置」という訳です。
続いて、ブランコを漕ぐ動作を繰り返す場合について考えていきます。ここまでの結果から、$\theta_{0}$の位置から始めて「最適な位置」でブランコを漕いだら$\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{\frac{3}{2}}$倍の角度の位置に帰ってくることになります。つまり$N$回だけ「最適な位置」でブランコを漕いだ後の角度$\theta_{N}$は$\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{\frac{3}{2}N}$となります。これより、$\log _{10} 0.9 \fallingdotseq-0.046 $ および $\log _{10} 2 \fallingdotseq 0.30$ を既知とすれば、最初の位置から2倍の角度の位置に達するには5回だけブランコを漕げばよいことが分かります(計算方法は以下の通り)。
微小角でない場合は?
ブランコの振れ幅が微小角でない場合は余弦の近似の妥当性がやや気になります。近似を適用せず余弦をそのまま用いた場合は、$$\small \cos \theta^{\prime \prime} =-\left\{\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{3}-1\right\}\cos \theta^{\prime}+\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{3} \cos\theta_{0}$$となるので、$\theta^{\prime}=0$ を代入した$$\small \theta^{\prime \prime}_{\text{max}}=\arccos\left\{-\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{3}+1+\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{3}\cos\theta_{0}\right\}$$で与えられます($\theta^{\prime}=0$ で$\cos \theta^{\prime}$は最大)。これと$\left(\dfrac{\ell}{\ell-\Delta \ell}\right)^{\frac{3}{2}} \theta_{0}$の値がどれだけ近いかを調べれば近似の妥当性が議論できそうです。
※ここで$\arccos$は$\cos$の逆関数(逆三角関数)です。
近似値/厳密値の比を関数と見なして横軸を初期角$\theta_{0}$(単位がラジアンなので注意)としてプロットすると以下のようになります。値が$1$に近いほど精度よく近似できていることになります。グラフ中のスライダーで $a=\dfrac{\Delta \ell}{\ell}$ の値を変えられます。
例えば、$\dfrac{\Delta \ell}{\ell}=0.1$ 程度であれば $\theta_{0}=10^{\circ}$のとき近似値/厳密値の比は $0.999526…$ となり、5回だけ「最適な位置」でブランコを漕いだ後の角度を計算すると、近似値では$2.209072…$倍、厳密値では$2.203845…$倍になります。誤差がかなり小さいことが分かりますね。
以上のことから、あまりにも初期角$\theta_{0}$が大きくない限り、$\cos \theta \fallingdotseq 1-\dfrac{\theta^{2}}{2}$ という近似はうまく機能することが観察されます。よく知られていることだと思いますが、この近似は振り子運動を単振動として近似するものです。
※現実には空気抵抗が存在し、回転軸とブランコの鎖の間にも摩擦が生じるので、これら力の影響まで考慮すればモデルはもっと複雑になります。
(余談)巨大ブランコ
余談ですが、2021年現在で世界一高いブランコは、中国の重慶にあるジオパーク「雲陽龍缸国家地質公園」のアトラクションとして整備された高さ328フィート(約100メートル)のブランコで、ギネス世界記録に登録されています。これが一般公開される前は南アフリカの “B!G RUSH” という高さが約80メートルの巨大ブランコが世界最高記録でした。
 図.雲陽龍缸国家地質公園のブランコ
図.雲陽龍缸国家地質公園のブランコ
これは極端な例ですが、$\ell = 100 \mathrm{~m}$ もあれば、ブランコの運動に伴う角度の変化はごく微小なので単振動として問題なく近似できますね。
因みに、世界一高い回転ブランコの記録は、ここ数年の間 “Orlando StarFlyer“(450フィート)が保持していましたが、ドバイの “Bollywood Parks Dubai” という遊園地にある “Bollywood Skyflyer“(460フィート=約140メートル)が今年に入って記録を塗り替えています。このドバイの遊園地には今年中に世界最大の観覧車がオープンし、ラスベガスの “HIGH ROLLER” の記録(550フィート)を更新するとのことです。
